RBSE Class 11 Maths Important Questions Chapter 7 क्रमचय और संचयं

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 7 क्रमचय और संचयं Important Questions and Answers.

RBSE Class 11 Maths Chapter 7 Important Questions क्रमचय और संचयं

अतिलघूतरात्मक प्रश्न- 

प्रश्न 1.
∠4, ∠5 तथा ∠6 का ल.स. लिखिए ।
हल:
ल.स. = ∠6

प्रश्न 2.
तीन मनुष्यों के बीच 4 कोट, 5 कमीज व 6 टोप हैं । वे इन्हें कितने प्रकार से पहन सकते हैं?
हल:
अभीष्ट प्रकार = ⁴P₃ × ⁵P₃ × ⁶P₃
= 4.3.2 × 5.4.3 × 6.5.4
= 172800

प्रश्न 3.
यदि n वस्तुओं में से, p वस्तुएँ एक प्रकार की, 9 वस्तुएँ दूसरे प्रकार की, r तीसरे प्रकार की तथा अन्य भिन्न-भिन्न हैं, तो क्रमचयों की संख्या लिखिए।
हल:
\(\frac{n !}{p ! q ! r !}\)

प्रश्न 4.
यदि ⁿP₆ = 30 × ⁿP₄, तो n का मान लिखिए ।
हल:

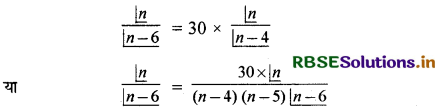
या (n - 4) (n - 5) = 30
या n² - 9n - 10 = 0
(n - 10) (n + 1) = 0
∴ n = 10

प्रश्न 5.
ⁿC_r + ⁿC_{r - 1} का मान लिखिए ।
हल:
^{n + 1}C_r

प्रश्न 6.
क्रिकेट के 12 खिलाड़ियों में से 9 की टीम कितने प्रकार से बनाई जा सकती है जबकि कप्तान सदैव रहे ?
हल:
¹¹C₈ = \(\frac{11 \times 10 \times 9}{3.2 .1}\) [∵ ¹¹C₈ = ¹¹C₃]
= 11 × 5 × 3 = 165

प्रश्न 7.
5 लड़के और 5 लड़कियों को कितने प्रकार से गोल मेज के चारों ओर बिठाया जा सकता है जबकि कोई दो लड़कियाँ एक साथ न बैठें ?
हल:
∠5.∠4

प्रश्न 8.
10 व्यक्तियों को एक गोल मेज के चारों ओर कितने प्रकार से बिठाया जा सकता है जबकि किन्हीं दो क्रमों में सबके पड़ौसी समान न हों ?
हल:
∠9 = 362880.

प्रश्न 9.
किसी विद्यार्थी के लिए 9 विषयों में से 5 विषय चयन के कितने तरीके होंगे, यदि दो (2) विषय अनिवार्य हों?
हल:
⁷C₃ = \(\frac{7.6 .5}{3.2 .1}\) = 35

प्रश्न 10.
यदि ⁿC₁₀ = ⁿC₁₂ तो n का मान ज्ञात करें तब ⁿC₅ का मान लिखें।
हल:
ⁿC₁₀ = ⁿC₁₂
या तो 10 = 12 जो सम्भव नहीं है।
या n = 10 + 12 = 22
∴ ²²C₅ = \(\frac{22 \times 21 \times 20 \times 19 \times 18}{1 \times 2 \times 3 \times 4 \times 5}\)
= 26334.

प्रश्न 11.
एक व्यक्ति, छः दोस्तों को आमंत्रित करना चाहता है। कितनी विधियों से वह उन्हें आमंत्रण भेज सकता है यदि वह तीन नौकरों को रखता है?
हल:
चूँकि एक कार्ड तीन नौकरों में से किसी भी एक द्वारा भेजा जा सकता है अत: पहले मित्र को आमंत्रण पत्र भेजने की विधियाँ = 3 इसी प्रकार छ: मित्रों का आमंत्रण पत्र भेजने हेतु 3 विधियाँ हैं।
अत: वांछित विधियों की संख्या
= 3 × 3 × 3 × 3 × 3 × 3
= 3⁶ = 729

प्रश्न 12.
सिद्ध करो कि-
ⁿP_n = 6. ⁿP_{n - 3}
हल:

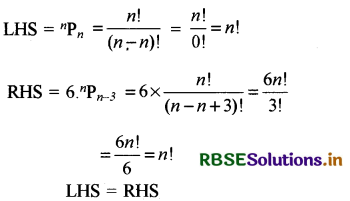
प्रश्न 13.
यदि (n + 2)! = 20n! तो n का मान ज्ञात कीजिये।
हल:
(n + 2)! = 20n!
⇒ (n + 2) (n + 1) n! = 20n !
⇒ (n + 2) (n + 1) = 20
⇒ n² + 3n - 18 = 0
⇒ (n + 6) ( n - 3) = 0
⇒ n = 3, -6
n = - 6 असम्भव है, अत: n = 3 होगा।

प्रश्न 14.
कितनी विधियों से 6 सेबों को 3 लड़कों के मध्य बाँटा जा सकता है, प्रत्येक लड़के को सेब प्राप्त करने का कोई प्रतिबन्ध नहीं है?
हल:
प्रत्येक सेब 3 लड़कों में से किसी को भी दिया जा सकता है और यह 3 विधियों से हो सकता है
इसलिये कुल विधियों की संख्या = 3⁶
= 3 × 3 × 3 × 3 × 3 × 3
= 27 × 27
= 729

प्रश्न 15.
12 व्यक्तियों में से 4 व्यक्तियों को कितनी विधियों से चुन सकते हैं जिसमें कि शर्त यह है कि एक विशिष्ट व्यक्ति अवश्य शामिल होना चाहिए ।
हल:
समूहों की संख्या ¹¹C₃ = \(\frac{11 \times 10 \times 9}{1 \times 2 \times 3}\)
= 165

प्रश्न 16.
एक स्कूल के छात्र संघ की बैठक में 18 छात्र उपस्थित हुए । प्रत्येक एक-दूसरे से केवल एक बार ही हाथ मिलाता है। कुल हाथ मिलाने वालों की संख्या ज्ञात करें।
हल:
छात्रों की संख्या 18
यहाँ प्रत्येक छात्र दूसरे छात्र से केवल एक बार हाथ मिलाता है। एक समय में 18 में से दो-दो समूह की संख्या हमें प्राप्त करनी है।
इसलिये हाथ मिलाने वालों की संख्या = ¹⁸C₂ = \(\frac{18 \times 17}{1 \times 2}\)
= 9 × 17
= 153

लघूत्तरात्मक प्रश्न-

प्रश्न 1.
निम्नलिखित को सिद्ध कीजिये-
(i) ⁿP_r = n . ^{n - 1}P_{r - 1} = n (n - 1) ^{n - 2}P_{r - 2}
हल:

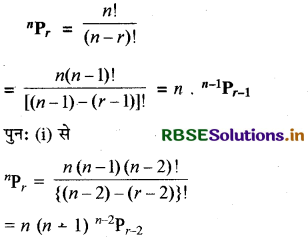
(ii) n. ⁿP_r = n (n - r + 1) ⁿP_{r - 1}
हल:

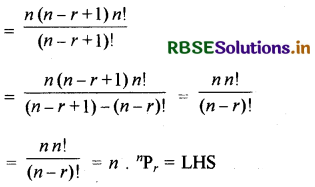
प्रश्न 2.
सिद्ध कीजिये कि
ⁿP_r = ^{n - 1}P_r + r ^{n - 1}P_{r - 1}
हल:

प्रश्न 3. n का मान ज्ञात कीजिये यदि
^{2n + 1}P_{n - 1} : ^{2n - 1}P_n = 3 : 5
हल:

⇒ 10 (2n + 1) = 3 (n + 2) (n + 1)
⇒ 20n + 10 = 3 (n² + 3n + 2)
⇒ 3n² - 11n - 4 = 0
⇒ (3n + 1) (n - 4) = 0, n = - \(\frac{1}{3}\), या 4
n का मान ऋणात्मक नहीं हो सकता है। अत: n = 4

प्रश्न 4.
यदि ²²P_{r + 1} : ²⁰P_{r + 2} = 11 : 52, तो r का मान ज्ञात कीजिए।
हल:
∵ ²²P_{r + 1} : ²⁰P_{r + 2} = 11 : 52

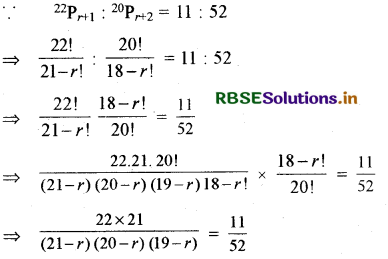
⇒ (21 − r) (20 − r) (19 − r) = 2 × 21 × 52
⇒ (21 − r) (20 − r) (19 − r) = 2 × 3 × 7 × 4 × 13
⇒ (21 − r) (20 − r) (19 − r) = 12 × 13 × 14
⇒ (21 − r) (20 − r) (19 − r) = (21 - 7) ( 20 - 7) (19 - 7)
⇒ r = 7

प्रश्न 5.
⁵⁰C₁₁ + ⁵⁰C₁₂ + ⁵¹C₁₃ - ⁵²C₁₃ का मान ज्ञात कीजिए।
हल:
प्रश्नानुसार ⁵⁰C₁₁ + ⁵⁰C₁₂ + ⁵¹C₁₃ - ⁵²C₁₃
(⁵⁰C₁₂ + ⁵⁰C₁₁) + ⁵¹C₁₃ - ⁵²C₁₃
अब सूत्र ⁿC_r + ⁿC_{r - 1} = ^{n + 1}C_r से
= ⁵¹C₁₂ + ⁵¹C₁₃ - ⁵²C₁₃
= (⁵⁰C₁₃ + ⁵¹C₁₂) - ⁵²C₁₃
= ⁵²C₁₃ - ⁵²C₁₃ = 0

प्रश्न 6.
एक माला बनाने में 10 विभिन्न मोती कितने प्रकार से पिरोए जा सकते हैं जबकि उनमें से चार विशेष मोती कभी भी पृथक् नहीं रहें ।
हल:
प्रश्नानुसार चार विशेष मोतियों को एक ही मोती मानने पर सबसे पहले हमें सात मोती पिरोने होंगे अर्थात् एक स्थिति चारों मोतियों के एक साथ वाली तथा छः शेष बचे मोती । अब यदि मोती दक्षिणावर्त दिशा में पिरोए जाते हैं तो माला को दूसरी ओर बदलने पर ये वामावर्त दिशा में हो जाते हैं । इस प्रकार दक्षिणावर्त और वामावर्त दिशाओं से केवल एक ही क्रम प्राप्त होता है तथा जो 4 विशेष मोती एक साथ रहते हैं, वे भी 24 प्रकार से अपने विन्यास बदल सकते हैं। अत: अभीष्ट विन्यास

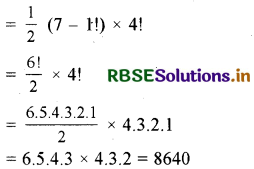
प्रश्न 7.
सिद्ध कीजिए \(\frac{2 n !}{n !}\) = {1.3.5 ....................... (2n - 1)}2ⁿ
हल:
यहाँ \(\frac{2 n !}{n !}\)

प्रश्न 8.
किसी मेजबान ने अपने घर पार्टी में 20 मेहमानों को आमंत्रित किया| ये 20 मेहमान तथा मेजबान किसी गोलाकार मेज पर खाना खाने के कितने तरीके से बैठ सकते हैं तथा क्रमचयों की संख्या कितनी होगी, यदि मेहमानों में से 2 विशेष व्यक्ति मेजबान के दोनों तरफ बैठें ?
हल:
(i) मेजबान सहित कुल 21 व्यक्तियों को गोलाकार मेज के चारों ओर बिठाने का अभीष्ट प्रकार
= 21 - 1! = 20!

(ii) माना G₁ तथा G₂ विशेष मेहमान हैं जो कि मेहमान के दोनों तरफ बैठते हैं
अर्थात् G₁HG₂; G₂HG₁
∵ 21 व्यक्तियों में से इन तीन को एक मानने पर व्यक्तियों की संख्या
= 21 - 3 + 1 = 19
∴ अभीष्ट क्रमचय = 19 - 1 ! × 2
= 18! × 2
= 2 18!

प्रश्न 9.
एक सन्दूक में दो सफेद, तीन काली व चार लाल गेंदें हैं। इस सन्दूक से तीन गेंदें कितनी विधियों से निकाली जा सकती हैं, जिनमें कम से कम एक काली गेंद अवश्य हो?
हल:
सन्दूक में कुल गेंदें = 2 + 3 + 4 = 9 जिनमें तीन काली तथा 6 अन्य गेंदें हैं।
अतः
स्थिति (i) जब एक काली व 2 अन्य गेंदें आएँ तो कुल तरीके
= ⁶C₂ × ³C₁ = \(\frac{6.5}{2.1}\) × 3 = 45
स्थिति (ii) यदि दो काली व एक अन्य गेंद आए तो कुल तरीके
= ⁶C₁ × ³C₂ = 6 × \(\frac{3.2}{2.1}\) = 18
स्थिति (iii) यदि तीनों ही गेंदें काली आएँ तो कुल तरीके
= ³C₃ = 1
∴ कुल तरीके (विधि) 45 + 18 + 1 64 

प्रश्न 10.
एक समतल में n बिन्दु हैं । इनमें से P बिन्दु एक सरल रेखा में है, किन्तु शेष में से कोई भी 3 बिन्दु एक रेखा में नहीं हैं। बताइये कि इन बिन्दुओं को मिलाने से कितने त्रिभुज बनाये जा सकते हैं?
हल:
किसी त्रिभुज को बनाने के लिये 3 बिन्दुओं की आवश्यकता होती है इसलिये यदि n बिन्दुओं में से कोई भी तीन बिन्दु एक सरल रेखा में न हों तो n बिन्दुओं से ⁿC₃ त्रिभुज बन सकते हैं | किन्तु P बिन्दु एक सरल रेखा में होने के कारण ^PC₃ त्रिभुज कम बनेंगे अतः त्रिभुज की अभीष्ट संख्या
= ⁿC₃ - ^pC₃
= \(\frac{n(n-1)(n-2)}{1.2 .3}\) - \(\frac{P(P-1)(P-2)}{1.2 .3}\)
= \(\frac{1}{6}\) [n (n - 1) (n - 2) - P (P - 1) (P - 2)]

निबन्धात्मक प्रश्न-

प्रश्न 1.
n का मान ज्ञात कीजिए, इस प्रकार कि
(i) ⁿP₅ = 42 ⁿP₃, n > 4
हल:
दिया है कि
ⁿP₅ = 42 ⁿP₃
या n (n - 1) (n - 2) (n - 3) (n - 4) = 42n (n - 1) (n - 2)
क्योंकि n > 4 इसलिए n (n - 1) (n - 2) ≠ 0
अतएव, दोनों पक्षों को n (n - 1) (n - 2), से भाग देने पर
(n - 3) (n - 4) = 42
या n² - 7n - 30 = 0
या n² - 10n + 3n - 30 = 0
या (n - 10 ) (n + 3) = 0
या n - 10 = 0 या n + 3 = 0
या n = 10 या n = - 3
क्योंकि n ऋण संख्या नहीं हो सकती है अंत: n = 10

(ii) \(\frac{{ }^n \mathbf{P}_4}{{ }^{n-1} \mathbf{P}_4}=\frac{5}{3}\), n > 4
हल:
दिया है कि \(\frac{{ }^n P_4}{{ }^{n-1} P_4}=\frac{5}{3}\)
इस प्रकार 3n (n - 1) (n - 2) ( n - 3) = 5(n - 1)
या 3n = 5 (n - 4)
[क्योंकि (n - 1) (n - 2) (n - 3) ≠ 0, n > 4]
या n = 10

प्रश्न 2.
9 स्त्रियों व 8 पुरुषों में से 12 सदस्यों की एक समिति बनानी है जिसमें कम से कम 5 स्त्रियों का होना आवश्यक है, तो उन समितियों की संख्या ज्ञात कीजिए। उन समितियों की संख्या भी ज्ञात कीजिए, यदि
(i) स्त्रियाँ बहुमत में हों ।
(ii) पुरुष बहुमत में हों ।
हल:
9 स्त्रियों में 8 पुरुषों में से 12 सदस्यों की समिति बनाने में, जबकि कम से कम 5 स्त्रियाँ अवश्य हों, तो निम्न स्थितियाँ सामने आती हैं-
स्थिति (i) यदि 9 स्त्रियाँ व 3 पुरुष हों, तो संख्या
= ⁹C₉ × ⁸C₃

स्थिति (ii) यदि 8 स्त्रियाँ व 4 पुरुष हों, तो संख्या
= ⁹C₈ × ⁸C₄ = ⁹C₁ × ⁸C₄

स्थिति (iii) यदि 7 स्त्रियाँ व 5 पुरुष हों, तो संख्या
= ⁹C₇ × ⁸C₅ = ⁹C₂ × ⁸C₃

स्थिति (iv) यदि 6 स्त्रियाँ व 6 पुरुष हों, तो संख्या
= ⁹C₆ × ⁸C₆ = ⁹C₃ × ⁸C₂

स्थिति (v) यदि 5 स्त्रियाँ व 7 पुरुष हों, तो संख्या
= ⁹C₅ × ⁸C₇ = ⁹C₄ × ⁸C₁

∴ अभीष्ट संख्या
= ⁹C₉ × ⁸C₃ + ⁹C₁ × ⁸C₄ + ⁹C₂ × ⁸C₃ + ⁹C₃ × ⁸C₂ + ⁹C₄ × ⁸C₁

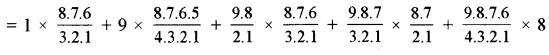
= 56+ 630 + 2016 + 2352 + 1008
= 6062

(i) यदि स्त्रियाँ अधिक हों, तो अभीष्ट संख्या
= स्थिति (i) + स्थिति (ii) + स्थिति (iii)
= 56 + 630 + 2016 = 2702

(ii) यदि पुरुष, स्त्रियों से अधिक हों, तो अभीष्ट संख्या
= स्थिति (v) = 1008

प्रश्न 3.
DELHI शब्द से अक्षरों से कितने शब्द बनाये जा सकते हैं, यदि
(i) सभी अक्षर लिये जायें
(ii) 3 अक्षर ही लिये जायें
(iii) प्रत्येक शब्द D से प्रारंभ हो
(iv) प्रत्येक शब्द D से आरंभ हो तथा I पर समाप्त हो
(v) दोनों स्वर साथ-साथ आयें
(vi) प्रत्येक शब्द दोनों स्वर से प्रारंभ हो।
हल:
DELHI में सभी अक्षर भिन्न-भिन्न हैं।

(i) सभी 5 अक्षरों को लेकर बनाये गये क्रमचयों की संख्या होगी
= ⁵P₅ = 5!
= 5 × 4 × 3 × 2 × 1
= 120

(ii) यदि 5 में से 3 अक्षर ही लिये जायें तो शब्दों की संख्या
= ⁵P₃ \(\frac{5 !}{2 !}=\frac{120}{2}\) = 60

(iii) प्रत्येक शब्द के प्रारंभ में D आता है तो फिर D स्थिर हो जाता है और इसलिये हमें केवल 4 अक्षरों को ही व्यवस्थित करना है अतः शब्दों की संख्या होगी = ⁴P₄ = 4!
= 4 × 3 × 2 × 1 = 24

(iv) प्रत्येक शब्द D से प्रारंभ हो तथा I पर समाप्त हो, तो फिर D तथा I स्थिर हो जाते हैं और इसलिये हमें केवल 3 अक्षरों को ही व्यवस्थित करना है । अतः शब्दों की संख्या होगी
= ³P₃ = 3! = 3 × 2 × 1 = 6

(v) जब दोनों स्वर साथ-साथ रखने हैं तो इनको एक अक्षर (EI) की तरह मान सकते हैं। अतः हमारे पास 4 अक्षर होंगे।
⁴P₄ = 4! = 24 विधियों से व्यवस्थित कर सकते हैं अर्थात् (EI) में भी दो अक्षर हैं जिनको साथ-साथ रखने में (EI) या (IE) ले सकते हैं अर्थात् इसे भी 2! = 2 विधियों से व्यवस्थित कर सकते हैं । इस प्रकार कुल शब्दों की संख्या = 2 × 24 = 48

(vi) प्रत्येक शब्द के प्रारम्भ में दोनों स्वर आते हैं, तो E तथा I (प्रथम दो स्थान पर) स्थिर हो जाते हैं और इसलिये हमें केवल 3 अक्षर को ही व्यवस्थित करना है जिन्हें ³P₃ = 3! = 6 विधियों से व्यवस्थित कर सकते हैं। लेकिन स्वर E तथा I को भी प्रथम दो स्थान पर 2! = 2 विधियों से व्यवस्थित कर सकते हैं। इस प्रकार से कुल शब्दों की संख्या होगी = 2 × 6 = 12

प्रश्न 4.
14 खिलाड़ियों में से एक क्रिकेट टीम के 11 खिलाड़ियों को कितने प्रकार चुना जा सकता है? कितनी बार एक विशेष खिलाड़ी
(i) सदैव सम्मिलित किया जाता है।
(ii) कभी भी सम्मिलित नहीं किया जाता।
हल:
14 खिलाड़ियों में से 11 खिलाड़ियों को चुनने के तरीके
= ¹⁴C₁₁

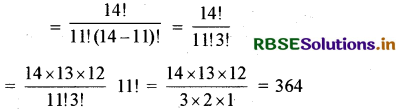
(i) जब एक विशेष खिलाड़ी को टीम में सदैव लेना है तो शेष बचे हुये 13 खिलाड़ियों में से 10 खिलाड़ियों को चुनना होगा । अतः 13 में से 10 का चयन करने के अभीष्ट तरीके होंगे
= ¹³C₁₀ = 10!(13–10)!

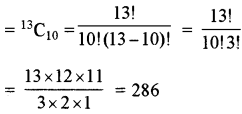
(ii) जब एक विशेष खिलाड़ी कभी भी नहीं लेना हो तो शेष 13 खिलाड़ियों में से 11 खिलाड़ियों को चुनना होगा। अतः इस - स्थिति में अभीष्ट तरीके होंगे-

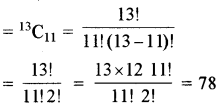
प्रश्न 5.
8 पुरुषों और 5 महिलाओं में से 6 सदस्यों की एक समिति बनानी है। यह समिति कितने प्रकार से बनाई जा सकती है जबकि प्रत्येक समिति में :
(i) केवल 2 पुरुष हों
(ii) केवल 2 महिलायें हों
(iii) कम से कम दो महिलायें हों
(iv) कम से कम दो पुरुष हों?
हल:
(i) 8 पुरुषों में से केवल 2 पुरुष ⁸C₂ तरीके से चुने जा सकते हैं तथा शेष 4 को 5 महिलाओं में से लेना है जो कि ⁵C₄ प्रकार से चुने जा सकते हैं । अतः अभीष्ट संख्या
= ⁸C₂ × ⁵C₄ = 28 × 5 = 140

(ii) 5 महिलाओं में से केवल 2 महिलाओं को SC 2 प्रकार से चुन सकते हैं तथा शेष 4 को 8 पुरुषों में से लेना है जो कि SC 4 प्रकार से चुन सकते हैं ।
अतः अभीष्ट संख्या = ⁵C₂ × ⁸C₄ = 10 × 70 = 700

(iii) कम से कम दो महिलाओं को लेने के लिये निम्नलिखित प्रकार से चुनाव कर सकते हैं :
2 महिलायें व 4 पुरुष, 3 महिलायें व 3 पुरुष, 4 महिलायें व 2 पुरुष, 5 महिलायें व 1 पुरुष अतः इनका चयन निम्न प्रकार से होगा
⁵C₂ × ⁸C₄, ⁵C₃ × ⁸C₃, ⁵C₄ × ⁸C₂, ⁵C₅ × ⁵C₁
अतः अभीष्ट संख्या
= ⁵C₂ × ⁸C₄ + ⁵C₃ × ⁸C₃ + ⁵C₄ × ⁸C₂ + ⁵C₅ × ⁸C₁
= 70 + 560 + 140 + 8 = 1408

(iv) उपर्युक्त विधि से कम से कम 2 पुरुष लेकर 6 सदस्यों की समिति बनाने की कुल विधियाँ होंगी-
= ⁸C₂ × ⁵C₄ + ⁸C₃ × ⁵C₃ + ⁸C₄ × ⁵C₂ + ⁸C₅ × ⁵C₁ + ⁸C₆
= 140 + 560 + 700 + 280 + 28 = 1708

बहुचयनात्मक प्रश्न-

प्रश्न 1.
यदि ⁿP_{n - 2} = 60 हो, तो n का मान होगा-
(A) 2
(B) 4
(C) 5
(D) 3
हल:
(C) 5

प्रश्न 2.
ⁿP_r ÷ ⁿC_r बराबर है-
(A) n!
(B) (n – r)!
(C) \(\frac{\mathrm{1}}{r !}\)
(D) r!
हल:
(D) r!

प्रश्न 3.
5 व्यक्ति एक गोल मेज पर कितने प्रकार से बैठ सकते हैं:
(A) 120
(B) 24
(C) 60
(D) 12
हल:
(B) 24

प्रश्न 4.
BHILWARA के अक्षरों से कितने शब्द बनाए जा सकते हैं :
(A) \(\frac{8 !}{2 !}\)
(B) 8!
(C) 7!
(D) \(\frac{6 !}{2 !}\)
हल:
(A) \(\frac{8 !}{2 !}\)

प्रश्न 5.
⁴⁷C₄ + \(\sum_{r=1}^5\) ^{52 - r}C₃ बराबर हैं:
(A) ⁵¹C₄
(B) ⁵²C₄
(C) ⁵³C₄
(D) इनमें से कोई नहीं
हल:
(B) ⁵²C₄

प्रश्न 6.
⁶¹C₅₇ - ⁶⁰C₅₆ का मान है।
(A) ⁶¹C₅₈
(B) ⁶⁰C₅₇
(C) ⁶⁰C₅₈
(D) ⁶⁰C₅₆
हल:
(B) ⁶⁰C₅₇

प्रश्न 7.
यदि ¹⁵C_3r = ¹⁵C_r+3, तो r बराबर है :
(A) 5
(B) 4
(C) 3
(D) 2
हल:
(C) 3

प्रश्न 8.
एक वृत्त की परिधि पर 6 बिन्दु हैं, इनको मिलाने वाली सरल रेखाओं की संख्या होगी:
(A) 30.
(B) 15
(C) 12
(D) 20
हल:
(B) 15

प्रश्न 9.
BHOPAL के अक्षरों से कितने शब्द बनाए जा सकते हैं ?
(A) 124
(B) 240
(C) 360
(D) 720
हल:
(D) 720

प्रश्न 10.
एक वृत्त की परिधि पर 4 बिन्दु हैं, इनको मिलाकर कितने त्रिभुज बनाए जा सकते हैं:
(A) 4
(B) 6
(C) 8
(D) 12
हल:
(A) 4

प्रश्न 11.
यदि ⁿC_r, r वस्तुओं को एक साथ लेकर n वस्तुओं के संचय की
संख्या को प्रदर्शित करता है, तो व्यंजक ⁿC_{r + 1} + ⁿC_{r - 1} + 2 × ⁿC_r बराबर है-
(A) ⁿ⁺²C_r
(C) ⁿ⁺²C_r+1
(B) ⁿ⁺¹C_r
(D) ⁿ⁺¹C_r+1
हल:
(B) ⁿ⁺¹C_r

प्रश्न 12.
शब्द GARDEN के अक्षरों से कितने शब्द बनाये जा सकते हैं ताकि स्वर वर्णक्रम में हों?
(A) 360
(B) 240
(C) 120
(D) 480
हल:
(A) 360

प्रश्न 13.
EXAMINATION के अक्षरों के कितने शब्द बनाए जा सकते हैं:
(A) \(\frac{9 !}{2 ! 2 ! 2 !}\)
(B) \(\frac{11 !}{2 ! 2 ! 2 !}\)
(C) \(\frac{11 !}{2 ! 2 !}\)
(D) उपर्युक्त में से कोई नहीं
हल:
(B) \(\frac{11 !}{2 ! 2 ! 2 !}\)

प्रश्न 14.
एक कार्यालय में क्लर्कों के 16 पद रिक्त हैं। 20 आवेदनकर्ताओं में से इन्हें कितने प्रकार से भरा जा सकता है ?
(A) 13800
(B) 969
(C) 13876
(D) 4845
हल:
(D) 4845

प्रश्न 15.
एक संस्था में एक पुरुष तथा एक महिला की आवश्यकता है। यदि 10 महिलाएँ तथा 15 पुरुष आवेदन करें, तो कितने प्रकार से चयन किया जा सकता है?
(A) 125
(B) 150
(C) 145
(D) 180
हल:
(B) 150

प्रश्न 16.
n! का मान है-
(A) n × n - 1!
(B) (n - 1 ) × n!
(C) n(n - 1)!
(D) उपर्युक्त में से कोई नहीं
हल:
(A) n × n - 1!

प्रश्न 17.
0! का मान बराबर होता है :
(A) अनन्त
(B) एक
(C) शून्य
(D) परिभाषित नहीं
हल:
(B) एक

प्रश्न 18.
यदि ⁿC₇ = ⁿC₄ हो, तो n का मान होगा-
(A) 11
(B) 7
(C) 4
(D) 5
हल:
(A) 11

प्रश्न 19.
शब्द PENCIL के अक्षरों को कितने तरीके से व्यवस्थित किया जा सकता है, यदि N हमेशा E के पश्चात् आए ?
(A) 420
(B) 720
(C) 120
(D) 520
हल:
(C) 120

प्रश्न 20.
शब्द COMBINE में विषम स्थानों पर स्वरों को रखते हुए और सभी अक्षरों को लेते हुये क्रमचयों की संख्या है-
(A) 96
(B) 144
(C) 512
(D) 576
हल:
(D) 576

प्रश्न 21.
INDIA शब्द के अक्षरों से बनने वाले कुल कितने शब्द होंगे ?
(A) 50
(B) 60
(C) 40
(D) 80
हल:
(B) 60

प्रश्न 22.
यदि ¹⁸C_r = ¹⁸C_{r + 2} तो ^rC₅ का मान होगा-
(A) 66
(B) 56
(C) 46
(D) 64
हल:
(B) 56

प्रश्न 23.
एक बहुभुज में 44 विकर्ण हैं । भुजाओं की संख्या होगी-
(A) 7
(B) 8
(C) 9
(D) 11
हल:
(D) 11

प्रश्न 24.
किसी बस में 3 पुरुषों और 2 महिलाओं के बैठने के तरीकों की. संख्या, जबकि प्रत्येक और बैठने वाले पुरुषों और महिलाओं की संख्या 3 है, होगी -
(A) 5!
(B) ⁶C₅ × 5!
(C) 6! × ⁶C₅
(D) 5! + ⁶C₅
हल:
(B) ⁶C₅ × 5!

प्रश्न 25.
यदि ^{n - 1}C₃ + ^n-1C₄ > ⁿC₃ तब x का मान होगा ----
(A) 7
(B) < 7 (C) > 7
(D) None
हल:
(C) > 7

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
यदि एक घटना m भिन्न तरीकों से घटित हो सकती है, तदोपरान्त एक अन्य घटना n भिन्न तरीकों से घटित हो सकती है, तो दिए हुए क्रम में दोनों घटनाओं के भिन्न तरीकों के घटित होने की कुल भिन्न संख्या .................................... है।
हल:
m × n

प्रश्न 2.
............................................ एक निश्चित क्रम में बना विन्यास है, जिसको दी हुई वस्तुओं में से एक समय में कुछ या सभी को लेकर बनाया गया है।
हल:
क्रमचय

प्रश्न 3.
n विभिन्न वस्तुओं में से एक समय में वस्तुओं को लेकर बनाए गए क्रमचयों की संख्या ......................................... होती है।
हल:
ⁿP_r

प्रश्न 4.
∠0 = ................................
हल:
1

प्रश्न 5.
n विभिन्न वस्तुओं में से एक समय r वस्तुओं को लेकर बने क्रमचयों की संख्या, जबकि वस्तुओं की पुनरावृत्ति की अनुमति हो, .................................... होती है ।
हल:
n^r

प्रश्न 6.
n विभिन्न वस्तुओं में से एक समय में वस्तुओं को लेकर बनने वाले संचयों की संख्या ..................................... होती है।
हल:
ⁿC_r

प्रश्न 7.
ⁿC_r + ⁿC_{r - 1} = .............................
हल:
^{n + 1}C_r

प्रश्न 8.
ⁿC_r = ......................................
हल:
\(\frac{\lfloor n}{\lfloor r\lfloor n-r}\)

प्रश्न 9.
ⁿC_x = ⁿC_y ⇒ ......................... या ......................................
हल:
x = y या x + y = n

प्रश्न 10.
⁴³C_{r - 6} = ⁴³C_{3r + 1} हो तो का मान ................................... होगा।
हल:
12

निम्नलिखित कथनों के लिए सत्य/असत्य लिखिए-

प्रश्न 1.
(∠n + 1), 2 तथा n के मध्य किसी भी प्राकृत संख्या से विभाज्य है।
हल:
असत्य

प्रश्न 2.
तीन अंकों की कुल संख्या, जबकि किसी भी अंक की पुनरावृत्ति नहीं हो, 648 है।
हल:
सत्य

प्रश्न 3.
नौ अंकों की कुल संख्या, जबकि सभी अंक भिन्न-भिन्न हों, 9∠9 है|
हल:
सत्य

प्रश्न 4.
यदि P (5, r) = 2.P(6, r - 1), तब r = 4
हल:
असत्य

प्रश्न 5.
²²p_r+1 : ²⁰p_r+2 = 11 : 52 हो तब r = 8
हल:
असत्य

प्रश्न 6.
P(n, r) = nP (n - 1; r - 1)
हल:
सत्य

प्रश्न 7.
‘ORIENTAL’ शब्द के अक्षरों से तीन अक्षरों से बनने वाले कुल शब्द 336 हैं।
हल:
सत्य

प्रश्न 8.
C(n, 12) = C(n, 8 ) तब C (22, n) का मान 232 है।
हल:
असत्य

प्रश्न 9.
⁵C₁ + ⁵C₂ + ⁵C₃ + ⁵C₄ + ⁵C₅ का मान 31 है।
हल:
सत्य

प्रश्न 10.
(⁷C₀ + ⁷C₁) + (⁷C₁ + ⁷C₂) + ........................ + (⁷C₆ + ⁷C₇) का मान 2⁸ - 2 है।
हल:
सत्य

सही मिलान कीजिए-

भाग (A)	भांग (B)
1. 20Cr = 20Cr-10 है तब 18Cr का मान	(a) 3
2. 15C3r = 15Cr+3 तब r का मान	(b) 816
3. nC12 = nC8 तब n का मान	(c) 7
4 (a2-a)C2 = (a2-a)C4, तब a का मान	(d) 91
5.	(e) 3
6. np4 = 20 × np2 तब n का मान	(f) 14
7. 2n+1Pn-1:2n-1Pn = 3:5 तब n का मान	(g) 20
8. 15Pr-1:16Pr-2 = 3:4, तब r का मान	(h) 5
9. np5:np3 = 2:1, तब n का मान	(i) 4
10. यदि nc8 = nC6, तब nC2 का मान	(j) 0

हल:
1. (b)
2. (e)
3. (g)
4. (a)
5. (j)
6. (c)
7. (i)
8. (f)
9. (h)
10. (d)