RBSE Class 11 Maths Important Questions Chapter 7 Permutations and Combinations

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 7 Permutations and Combinations Questions and Answers.

RBSE Class 11 Maths Chapter 7 Important Questions Permutations and Combinations

Question 1.
How many words can be formed by taking 3 consonants and 3 vowels out of 8 consonants and 4 vowels?
Answer:
By taking 3 consonants and 3 vowels we have to formed 6 letter words
No. of ways to choose 3 consonants out of 8 = ⁸C₃
No. of ways to choose 3 vowels out of 4 = ⁴C₃
But, by changing order of 6 letters of each word it can be arrange by 6! ways
Thus, no., of combination of 3 consonants and 3 vowels = ⁸C₃ × ⁴C₃
Thus, required no. of words with 3 consonants and 3 vowels
= ⁸C₃ × ⁴C₃ × 6!

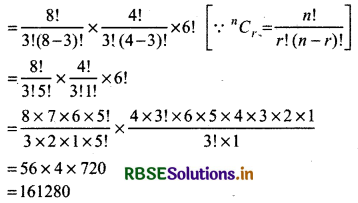
Thus, taking 3 consonants and 3 vowels no. of words formed = 161280.

Question 2.
How many ways 6 persons out of 4 teachers and 7 students, can be selected, when there must be
(i) only one teacher.
(ii) at least one teacher.
Answer:
(i) When there must be only one teacher.
In this case, 6 persons can be selected in the following ways:
1 teacher and 5 students
Now, no. of ways to select ¡ teacher out of 4 teachers = ⁴C₁
and no. of ways to select 5 students out of 7 students = ⁷C₅
Thus, total ways to select = ⁴C₁ × ⁷C₅

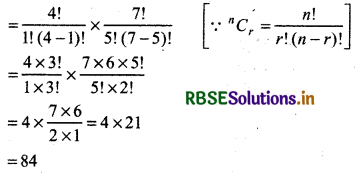
(ii) When at least one teacher is selected
In this case, 6 persons can be selected in the following ways
1 Teachers and 5 students can be select by = ⁴C₁ × ⁷C₅ ways
2 Teachers and 4 students can be select by = ⁴C₂ × ⁷C₄ ways
3 Teachers and 3 students can be select by = ⁴C₃ × ⁷C₃ ways
4 Teachers and 2 students can be select by = ⁴C₄ × ⁷C₂ ways
All four methods are mutually exclusive
Thus, total no. of ways of selection
= ⁴C₁ × ⁷C₅ + ⁴C₂ × ⁷C₄ + ⁴C₃ × ⁷C₃ + ⁴C₄ × ⁷C₂

= 2 × 7 × 6 + 6 × 35 + 4 × 35 + 1 × 21
= 84 + 210 + 140 + 21
= 455

Question 3.
How many ways 7 green and 5 yellow balls can be arrange in a row whereas any two yellow balls never placed together?
Answer:
Let each green ball is represented by 'H' .......
...H...H...H...H...H...H...H
If we placed 7 green balls in a row at same distance then:
We get total 8 places where yellow balls can placed with given condition as shown in above figure.
Thus, required method of selection
= No. of ways to fill 8 blank spaces with 5 yellow balls
= ⁸C₅ = \(\frac{8 !}{5 !(8-5) !}\) [∵ ⁿC_r = \(\frac{n !}{r !(n-r) !}\)]
= \(\frac{8 !}{5 ! 3 !}=\frac{8 \times 7 \times 6 \times 5 \times 4 \times 3 !}{5 \times 4 \times 3 ! \times 3 \times 2 \times 1}\) = 56

Question 4.
How many ways Mohan can invite at least one friend out of 4 friends for lunch?
Answer:
To invite at least 1 friend means he can invite 1 or 2 or 3 or 4 friends.
Thus, total no. of ways to invite the friends
= ⁴C₁ + ⁴C₂ + ⁴C₃ + ⁴C₄
= 4 + 6 + 4 + 1 = 15

Question 5.
There are 6 girls and 8 boys in a group then how many ways a team of 7 members can be selected. If team contains
(i) no girl.
(ii) at least 1 boy and 1 girl.
Answer:
(i) No girl in team
Then there will be all boys in team
Thus, selection of 7 boys out of 8 can be done by ⁸C₁ ways
Thus, total ways = ⁸C₇
= \(\frac{8 !}{7 !(8-7) !}\) [∵ ⁿC_r = \(\frac{n !}{r !(n-r) !}\)]
= \(\frac{8 \times 7 !}{7 ! \times 1 !}\) = 8

(ii) At least I boy and I girl
Then possible ways to select a team
(a) 6 boys and 1 girl
(b) 5 boys and 2 girls
(c) 4 boys and 3 girls
(d) 3 boys and 4 girls
(e) 2 boys and 5 girls
(f) 1 boy and 6 girls
No. of ways to select 6 boys and 1 girl = ⁸C₆ × ⁶C₁
No. of ways to select 5 boys and 2 girls = ⁸C₅ × ⁶C₂
No. of ways to select 4 boys and 3 girls = ⁸C₄ × ⁶C₃
No. of ways to select boys and 4 girls = ⁸C₃ × ⁶C₄
No. of ways to select 2 boys and 5'girls = ⁸C₂ × ⁶C₅
No. of ways to select 1 boy and 6 girls = ⁸C₁ × ⁶C₆
Thus, total no. of ways to -select team
= ⁸C₆ × ⁶C₁ + ⁸C₅ × ⁶C₂ + ⁸C₄ × ⁶C₃ + ⁸C₃ × ⁶C₄ + ⁸C₂ × ⁶C₅ + ⁸C₁ × ⁶C₆

= 28 × 6 + 8 × 7 × 15 + 70 × 20 + 56 × 15 + 28 × 6 + 8 × 1
= 168 + 840 + 1400 + 840 + 168 + 8
= 3424

Question 6.
Taking 8 men and 5 women, a committee of 6 members has to be formed. How many ways this committee can be formed whereas each committee:
(i) consist of only 2 men
(ii) consist of only 2 women
(iii) consist of at least 2 women
(iv) consist of at least 2 men
Answer:
(i) 2 men from 8 men can be selected by ⁸C₂ ways and rest 4 is taken from 5 women by ⁵C₄ ways.
∴ Required number = ⁸C₂ × ⁵C₄ = 28 × 5 = 140.

(ii) 2 women from S can be selected by ⁵C₂ ways and rest 4 from 8 men can be selected by ⁸C₄ ways.
∴ Required number = ⁵C₂ × ⁸C₄ = 10 × 70 = 700.

(iii) For taking at least 2 women, we can select by following ways:
2 women and 4 men, 3 women and 3 men,
4 women and 2 men, 5 women and I men
So these will be selected by
⁵C₂ × ⁸C₄; ⁵C₃ × ⁸C₃; ⁵C₄ × ⁸C₂; ⁵C₅ × ⁸C₁
ways respectively.
∴ Required number
⁵C₂ × ⁸C₄; ⁵C₃ × ⁸C₃; ⁵C₄ × ⁸C₂; ⁵C₅ × ⁸C₁
= 700 + 560 + 140 + 8 = 1408

(iv) From above method, by taking at least 2 men,
form a total number of ways :
⁸C₂ × ⁵C₄ + ⁸C₃ × ⁵C₃ + ⁸C₄ × ⁵C₂ + ⁸C₅ × ⁵C₁ + ⁸C₆
= 140 + 560 + 700 + 280 + 28
= 1436

Question 7.
How many 3-digit numbers less than 1000 can be formed using the digits 1, 2, 3, 4, 5, 6, if no digits ¡s repeated?
Answer:
Given number of digits 6
For forming 3-digit number, we have to choose of the three digit from these 6-digits.
Hence, total numbers which have 3 digits
= ⁶p₃ = \(\frac{6 !}{3 !}\) = \(\frac{6 \times 5 \times 4 \times(3) !}{(3) !}\)
= 6 × 5 × 4 = 120.

Question 8.
How many ways 15 members of a committee can sit around the round table whereas secretary sit on one side and vice secretary on other side of director?
Answer:
Total number of members 15
Here, the position of secretary, vice secretary and director are fixed but there is no condition of clockwise and anti clockwise
Hence, total number of sitting ways according to condition = 2 !
Now, we can change the position of 12 members only.
Hence, total number sitting ways of 12 members = 12!
Hence, total number of ways 15 members sit according to given condition.
= 12! × 2!

Question 9.
There are 15 stations on a railway line. For this, how many different tickets of a class should be printed such that any person from any station can buy ticket of other station of this line?
Answer:
Total number of stations = 15
A person buy a ticket on a station then we can buy tickets of remaining 14 stations.
Hence, total number of methods of printing 14 tickets out of 15 tickets.
= ¹⁵P₁₄ = \(\frac{15 !}{14 !}\) = \(\frac{15 \times 14 !}{14 !}\) = 15
∵ One ticket can be printed in 2 ways in this way total 14 tickets will be printed.
Hence, total number of ways tickets be printed for 15 stations are
= 15 × 14 = 210.

Question 10.
How many ways 10 different beads can be threads for making a garland wheareas 4 special beads never remain separate ?
Answer:
4 out of 10 beads do not remain together then Total remaining beads = 10 - 4 = 6
Hence, the methods of making a garland using 6 beads = 6!
If 4 out of 10 beads do not remain together then the method of making a garland = 6 ! × 4 !
As in a garland there is no difference between clockwise and anticlockwise, so, methods to make a garland with 10 different beads.
= \(\frac{6 ! \times 4 !}{2}\)
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 \times 4 \times 3 \times 2}{2}\)
= 8640.

Question 11.
How many numbers can be formed using digits 0,1,2,..,, 9 which is more than or equal to 6000 and less than 7000 and is divisible by 5 whereas any number can be repeated as many times ?
Answer:
The numbers which are more than or equal to 6000 and less than 7000 and is divisible by 5 has 6 on thousand’s place and 0 or 5 on one’s place and number is 4 digits number. As digits can be repeated.

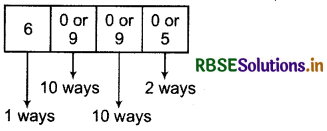
Hence, total numbers = 1 × 10 × 10 × 2
= 200

Question 12.
How many words can be formed from letters of word SCHOOL, whereas both O’s not come together ?
Answer:
There are total 6 letters in word SCHOOL.
In it there are 2 O’s and other letters are different then the number of total permutations = \(\frac{6 !}{2 !}\)
If 2 O’s take together then it will take as one letter then number of permutations taking 2 O’s together = 5 !
Hence, number of permutations when 2 O’s are not together are
= \(\frac{6 !}{2 !}\) - 5!
= \(\frac{6 \times 5 \times 4 \times 3 \times 2 !}{2 !}\) - 5!
= 6 × 5 × 4 × 3 - 5 × 4 × 3 × 2
= 360 - 120
= 240.

Question 13.
If the letters of the word ‘RANDOM’ are arranged in a dictionary in order then find the rank of this word.
Answer:
There are 6 letters in the word ‘RANDOM’ and in order of alphabet these comes ‘ ADMNOR’ so therefore
(i) no. of words start with 'A' are
A ××××× = 5! = 120
(ii) no. of words start with ‘D’ are
D ××××× = 5! = 120
(iii) no. of words start with ‘M' are
M××××× = 5! = 120 ,
(iv) no. of words start with 'N’ are
N ××××× = 5!=120
(v) no. of words start with ‘O' are
O××××× = 5! = 120
(vi) no. of words start with 'RAD' are
RAD××× = 3! = 6
(vii) no. of words start with ‘RAM’ are
RAM × × × = 3! =6
(viii) no. of words start with ‘RANDOM’ is
RANDOM × = 1
(ix) word next to the word RANDOM is RANDOM
so therefore rank of word ‘RANDOM’ is
120 + 120 + 120 + 120 + 120 + 6 + 6 + 1 + 1 = 614th

Question 14.
A box contains two white, three black and four red balls. Determine the number of ways in which three balls can be selected from this box, in which at least one black ball is compulsory.
Answer:
Total number of balls in the box
= 2 + 3 + 4 = 9
For at least one black ball we can choose it in the following ways :

White = 2	Black = 3	Red = 4
1	1	1
2	1	0
0	1	2
1	2	0
0	2	1
0	3	0

Total number of permutation according to the table
= (²C₁ × ³C₁ × ⁴C₁) + (²C₂ × ³C₁ × ⁴C₀) + (²C₀ × ³C₁ × ⁴C₁) + (²C₀ × ³C₃ × ⁴C₀)
+ (²C₀ × ³C₂ × ⁴C₁) + (²C₀ × ³C₃ × ⁴C₀)
= (2 × 3 × 4) + (1 × 3 × 1) + (1 × 3 × 6) + (2 × 3 × 1) + (1 × 3 × 4) + (1 × 1 × 1)
= 24 + 3 + 18 + 6 + 12 + 1
= 64

Question 15.
By 6 different coloured flags, taking one or more than one how many ways signal can be given ?
[Hint: ⁶C₁ × 1! + ⁶C₂ × 2! + ⁶C₃ × 3!
+ ⁶C₄ × 4! + ⁶C₅ × 5 ! + ⁶C₆ × 6 !]
Answer:
Total number of coloured flags = 6
Hence we can take any colour from 1 to 6.
Thus, the number of signals formed by using 6 different types of coloured flags
= ⁶C₁ × 1! + ⁶C₂ × 2! + ⁶C₃ × 3!
+ ⁶C₄ × 4! + ⁶C₅ × 5 ! + ⁶C₆ × 6 !
= 6 × 1 + 15 × 2 + 20 × 3 × 2 + 15 × 4 × 3 × 2 + 6 × 5 × 4 × 3 × 2 + 1 × 6 × 5 × 4 × 3 × 2
= 6 + 30+120 + 360 + 720 + 720
= 1956.

Question 6.
Number of diagonals in a polygon is 44 then find number of its sides.
Answer:
Number of diagonals = 44
Formula: Number of diagonals = \(\frac{n(n-3)}{2}\)
where n = number of sides.
⇒ \(\frac{n(n-3)}{2}\) = 44
⇒ n² - 3n = 88
⇒ n² - 3n - 88 = 0
On solving n = 11, -8
∵ Negative number is not possible.
Hence, number of sides = 11.

Question 17.
How many numbers can be formed taking 4 digits from digits 1, 2, 3, 4, 5, 6 whereas digit 4 and 5 are compulsory ?
Answer:
Total number of digits = 6
We have to take 4 digits but digit 4 and 5 are compulsory. Thus, we have to choose only 2 digits out of 6 - 2 = 4 digits.
Now, the numbers formed by using 4 digits is 4P4. Hence required number
= ⁴C₂ × ⁴P₄
= \(\frac{4 \times 3}{2 \times 1}\) × 4!
= 6 × 24 = 144

Question 18.
In how many ways 6 '+’ and 4 '-' sign can be kept in a line whereas any two occur together ?
Answer:
First we put '+’ in a line. This can be done in 1 way because all ‘+’ are same.
+ + + + + +
Now we put in the following way
- + - + - + - + - + -
Hence, the method of putting sign in 4 out of 7 places = ⁷c₄ × 1 because signs are same.
∴ Total number of ways 6 '+’ and 4 ‘-' sign occur together
= 1 × ⁷C₄ × 1
= \(\frac{7 !}{4 ! 3 !}\) = 35

Question 19.
By 8 students and 5 professors, we have to make a college council, taking 5 students and 2 professors. How many councils can be formed ?
Answer:
Number of methods of choosing 5 out of 8 students = ⁸C₅
and number of methods of choosing 2 out of 5 professors = ⁵C₂
∴ By the basic principle of calculation the methods of choosing 5 out of 8 students and 2 out of 5 professors are
= ⁸C₅ × ⁵C₂

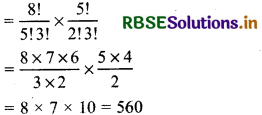
Hence, required councils are 560.

Question 20.
In how many ways can one select a cricket team of 11 from 14 players in which at least 2 bowlers are compulsory' whereas only 4 players can bowl. How many ways this team can be formed ?
Answer:
The method of choosing 2 out of 4 bowlers is ⁴C₂ and the method of choosing 9 out of remaining to players ¹⁰C₉. Similarly, we Can find the methods for 3 and 4 bowlers.
Hence, total number of ways to select 11 players out of 14 players
= ⁴C₂ × ¹⁰C₉ + ⁴C₃ × ¹⁰C₈ + ⁴C₄ × ¹⁰C₇

Question 21.
Find the number of chords passing through 11 points on circumference of a circle.
Answer:
Number of point on circumference of circle = 11
We know that a chord is formed by joining two points.
Hence taking 2 points out of 11 points number of chords
= ¹¹C₂

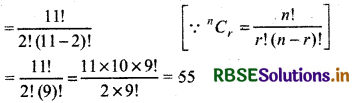
Hence, number of chords = 55.

Question 22.
There are n points in a plane in which m points are collinear. How many triangles will be formed by joining three points ?
Answer:
For making a triangle we need three points thus if 3 points out of n points are not in a line, then ⁿC₃ triangle can be formed by n points but m point is in a line, thus ^mC₃ triangle forms less.
Hence, required number of triangles
= ⁿC₃ - ^mC₃

Question 23.
Find the number of diagonals of a decagon.
Answer:
There are 10 vertices in a decagon. Now by joining two vertices we get a side of decagon or a diagonal.
Hence, number of line segment by joining of vertices of decagon = number of ways taking 2 points out of 10 points
= ¹⁰C₂ = \(\frac{10(10-1)}{2 !}\)
Now, there are 10 sides of decagon in ¹⁰C₂ line segment
∴ Required number of diagonals 

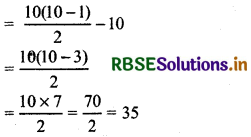
Hence, number of diagonals are 35.

Question 24.
There are 5 empty seats in a train, then in how many ways three travellers can sit on these seats ?
Answer:
Number of ways of seating of 3 travellers out of 5 seats.
= ⁵P₃
= \(\frac{5 !}{(5-3) !}\)
= \(\frac{5 \times 4 \times 3 \times 2 !}{2 !}\)
= 60
Hence, 3 travellers can be seated by 60 ways.

Question 25.
A group of 7 has to be formed from 6 boys and 4 girls. In how many ways group can be formed if boys are in majority in this group ?
Answer:
Number of boys = 6
Number of girls = 4
Number of members in the group = 7
One putting boys in majority in the group We have to choose in the following ways:
4 boys + 3 girls
5 boys + 2 girls
6 boys + 1 girl
Number of ways choosing 4 boys and 3 girls = ⁶C₄ × ⁴C₃
Number of ways choosing 5 boys and 2 girls = ⁶C₅ × ⁴C₂
Number of ways choosing 6 boys and 1 girl = ⁶C₆ × ⁴C₁
Required number of ways forming the group
= ⁶C₄ × ⁴C₃ + ⁶C₅ × ⁴C₂ + ⁶C₆ × ⁴C₁
= 15 × 4 + 6 × 6 + 1 × 4
= 60 + 36 + 4 = 100
Hence, group can be formed by 100 ways.

Question 26.
In the conference of 8 persons, every person handshake with each other only once, then find the total number of handshaked.
Answer:
When two persons shakes hand with each other, then this is taken as one handshake.
Hence, the number of handshake is equal to choosing 2 persons out of 8 persons.
∴ Number of handshaked
= ⁸C₂ = \(\frac{8 !}{2 !(8-2) !}=\frac{8 \times 7 \times 6 !}{2 \times 1 \times 6 !}=\frac{56}{2}\) = 28
Hence, required number of handshaked is 28.

Question 27.
In how many ways 6 men and 6 women can sit around the round table whereas any two women never sit together ?
Answer:
First we sit the men in a order that there is a place vacant between two men.
Then, number of ways sitting 6 men = (6 - 1)! = 5 !
Now number of ways sitting 6 women in the vacant places = 6 !
∴ Number of permutations = (6 - 1) ! = 5 !
Now, number of ways sitting 6 women in the vacant place = 6!
∴ Number of permutations = 5 ! × 6 !
= (5 × 4 × 3 × 2 × 1) × (6 × 5 × 4 × 3 × 2 × 1)
= 86400.

Multiple Choice Questions

Question 1.
¹²P₂ equals:
(a) 132
(b) 131
(c) 232
(d) None of these
Answer:
(a) 132

Question 2.
If ¹⁵P_r = 2730 then r equals:
(a) 6
(b) 3
(c) 9
(d) None of these
Answer:
(b) 3

Question 3.
If ⁹P_r = 60480 then r equals:
(a) 3
(b) 6
(c) 12
(d) None of these
Answer:
(b) 6

Question 4.
If 16. ⁿP₃ = 13. ^{n + 1}P₃, then n equals:
(a) 15
(b) 12
(c) 10
(d) None of these
Answer:
(a) 15

Question 5.
If ⁿP₆ = 30. ⁿP₄ then n equals:
(a) 10
(b) 5
(c) 8
(d) None of these
Answer:
(a) 10

Question 6.
If ⁿP₄ . ^{n - 1}P₃ = 9 : 1 then n equals:
(a) 9
(b) 6
(c) 12
(d) None of these
Answer:
(a) 9

Question 7.
ⁿC_r + ⁿC_{r + 1} equals:
(a) 9
(b) 5
(c) 12
(d) None of these
Answer:
(a) 9

Question 8.
ⁿP_r equals :
(a) r! × (ⁿC_r)
(b) \(\frac{{ }^n C_r}{r !}\)
(c) r.ⁿC_r
(d) None of these
Answer:
(a) r! × (ⁿC_r)

Question 9.
^{n - 1}C_r + ^{n - 1}C_{r - 1} equals :
(a) ⁿC_r
(b) ^{n - 1}C_2r
(c) ^{(2n - 1)}C_r
(d) None of these
Answer:
(a) ⁿC_r

Question 10.
No. of ways to select team of 11 players out of 14 players:
(a) 360
(b) 364
(c) 120
(d) None of these
Answer:
(b) 364

Question 11.
No. of ways 4 persons can sit at three empty seats:
(a) 4
(b) 6
(c) 8
(d) None of these
Answer:
(a) 4

Question 12.
Number of hexagon formed by taking 10 points on circumference of circle:
(a) 210
(b) 120
(c) 216
(d) None of these
Answer:
(a) 210

Question 13.
If ⁿC₅ = ⁿC₁ then ⁿP₃ equals:
(a) 12
(b) 6
(c) 18
(d) None of these
Answer:
(a) 12

Question 14.
If ²ⁿC₃ : ⁿC₂ = 44 : 3 then value of n is :
(a) 6
(b) 12
(c) 3
(d) None of these
Answer:
(a) 6

Question 15.
⁴⁷C₄ + \(\sum_{r=1}^5\) ^{(52 - r)}C₃ equals :
(a) ⁵²C₄
(b) ⁵²C₃
(c) ⁵²C₆
(d) None of these
Answer:
(a) ⁵²C₄

Question 16.
No. of ways to constitute a team of 11 members out of 6 teachers and 8 students :
(a) 364
(b) 120
(c) 168
(d) None of these
Answer:
(a) 364

Question 17.
If ⁿ⁺¹C₃ = 2. ⁿC₂ then n equals :
(a) 5
(b) 3
(c) 6
(d) None of these
Answer:
(a) 5

Question 18.
Find the total number of ways of distributing 5 different balls in to 3 boxes :
(a) 243
(b) 150
(c) 6
(d) 125
Answer:
(a) 243

Question 19.
Total ways to select pen out of 10 pens :
(a) 2¹⁰ - 1
(b) 2¹⁰
(c) 2⁹
(d) None of these
Answer:
(a) 2¹⁰ - 1

Question 20.
Number of 5 member committees out of 7 men and 7 women. In which at least 2 women exist in each committee is:
(a) 91
(b) 92
(c) 108
(d) None of these
Answer:
(d) None of these

Question 21.
Number of ways to kept 7 green and 5 red balls in a row whereas no two red balls exist together, are:
(a) 56
(b) 112
(c) 120
(d) None of these
Answer:
(a) 56

Question 22.
Number of combinations formed by 5 pens, 3 pencils and 4 rubber is :
(a) 119
(b) 120
(c) 60
(d) None of these
Answer:
(c) 60

Question 23.
No. of ways of 3 prize distribution to 6 players whereas any player can get how many prizes are:
(a) 6³
(b) 6⁴
(c) 6⁶
(d) None of these
Answer:
(a) 6³

Question 24.
Number of diagonals in hexagon is :
(a) 9
(b) 6
(c) 12
(d) None of these
Answer:
(a) 9

Question 25.
In a plane out of 12 points 5 are collinear, then triangle formed by these points are :
(a) 210
(b) 120
(c) 320
(d) None of these
Answer:
(a) 210

Question 26.
There are 4 letters and 4 envelopes with address when any 4 letters are not dropped in right envelope then total ways are :
(a) 9
(b) 10
(c) 16
(d) None of these
Answer:
(a) 9

Question 27.
There are 44 diagonals in a polygon then number of sides in polygon is:
(a) 11
(b) 7
(c) 8
(d) None of these
Answer:
(a) 11

Question 28.
Using letters of the word ‘EAMCET’ words sfre formed when two vowels are not together then number of words is :
(a) 72
(b) 144
(c) 360
(d) None of these
Answer:
(d) None of these

Question 29.
Number of ways to choose 5 white and 4 red balls out of 10 white and 8 red balls are :
(a) ¹⁰C₅ × ⁸C₄
(b) ⁸C₅ × ¹⁰C₄
(c) ¹⁰C₈ × ⁸C₅
(d) None of these
Answer:
(a) ¹⁰C₅ × ⁸C₄

Question 30.
930 Diwali cards are distributed among students of a class. Each student send card to each remaining student then number of student in a class is:
(a) 31
(b) 32
(c) 93
(d) None of these
Answer:
(a) 31

Fill in the blanks

Question 1.
The value of 0! = ................................
Answer:
1

Question 2.
The number of arrangement taken 5 at a time out of n distinct element (Repitition is allowed) ................................
Answer:
n⁵

Question 3.
If ⁿP_r = 840, ⁿc_r = 35 then r = ................................
Answer:
4

Question 4.
The value of ¹⁵C₈ + ¹⁵C₉ - ¹⁵C₆ - ¹⁵C₇ = ..........................................
Answer:
0

Question 5.
The number of six-digit number, all digits of which are odd is ...........................................
Answer:
5⁶

Question 6.
The number of diagonals of n sided polygon is .............................................
Answer:
(ⁿC₂ - n)

Question 7.
The number of possible out comes when a coin is tossed 6 times is .........................................
Answer:
2⁶

Question 8.
If ⁿC₁₀ = ⁿC₄ then value of n is ..............................................
Answer:
14

Question 9.
A convex polygon has 54 diagonals, then number of its sides are .......................................................
Answer:
12

Question 10.
Number of triangle are made from 15 collinear points ..................................................
Answer:
455

Question 11.
How many ways 5 girls and 3 boys be seated in a row so that no two boys are together ..............................................
Answer:
14400

Question 12.
100! = ..................................... 99.98.97!
Answer:
100

Question 13.
The value of 10.9! = .......................................
Answer:
10

Question 14.
The value of ⁿC_n = ..........................................
Answer:
1

Question 15.
The value of ⁿP_n = ............................................
Answer:
n!

State whether the statements True or False.

Question 1.
The Value of ⁵P₅ = 5
Answer:
False

Question 2.
The value of ¹⁰C₉ = 10
Answer:
True

Question 3.
If some or all of n objects are taken at a time, then number of combination is 2ⁿ - 1
Answer:
True

Question 4.
Three letters can be posted in five letter boxes is 35 ways.
Answer:
False

Question 5.
There are 12 points in a plane of which 5 points are collinear then the number of lines by joining these points in pairs is ¹²C₂ - ⁵C₂.
Answer:
False

Question 6.
The no. of arrangements when out of 10 different things 5 taken at a times is ¹⁰P₅.
Answer:
True

Question 7.
The number of selection when 2 men are selected from 5 men is ⁵C₂.
Answer:
True

Question 8.
The number of selection of n different thing taken 5 at a time is ⁿC₀.
Answer:
False

Question 9.
The number of arrangement always greater than the number of selections.
Answer:
False

Question 10.
If ⁿC_x = ⁿC_y, then x = n - y.
Answer:
True