RBSE Class 11 Maths Important Questions Chapter 6 Linear Inequalities

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 6 Linear Inequalities  Questions and Answers.

RBSE Class 11 Maths Chapter 6 Important Questions Linear Inequalities 

Question 1.
Solve the inequality - 5 ≤ 2x - 1 < 3.
Answer:
From - 5 ≤ 2x - 1 < 3, we get two inequalities
- 5 ≤ 2x - 1 and 2x - 1 < 3
To solve these inequalities we should make coefficient of variable x between given inequalities as I.
Now, - 5 ≤ 2x - 1 < 3
or - 5 + 1 ≤ 2x < 3 + 1(Replacing - 1 in both sides)
or - 4 ≤ 2x < 4

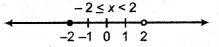
Thus, required solution of inequality
x ∈ [- 2, 2) - 2 ≤ x < 2

Question 2.
Solve: - 10 ≤ 6x - 4 < 8
Answer:
We have,
- 10 ≤ 6x - 4 < 8
⇒ - 10 + 4 ≤ 6x - 4 + 4 < 8 + 4
[Adding 4 on both sides]
⇒ - 6 ≤ 6x < 12 ⇒ - 1 ≤ x < 2
[Dividing both sides by 6]

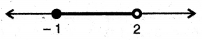
Thus, required solution of inequality x ∈ [- 1, 2)

Question 3.
Solve the inequality - 6 ≤ \(\frac{6-4 x}{3}\) ≤ 8
Answer:
- 6 ≤ \(\frac{6-4 x}{3}\) ≤ 8
Multiplying (i) by 3
- 6 × 3 ≤ 3 × \(\frac{(6-4 x)}{3}\) ≤ 3 × 8
or - 18 ≤ 6 - 4x ≤ 24
or - 18 - 6 ≤ - 4x ≤ 24 - 6
or - 24 ≤ - 4x ≤ 18
or - 6 ≤ - x ≤ \(\frac{9}{2}\) (Dividing by 4)
or 6 ≥ x ≥ - \(\frac{9}{2}\) [Multiplying by (- 1)]
or - \(\frac{9}{2}\) ≤ x ≤ 6
[Multiplying by (-1), sign ≤ converts into ≥]

Thus, solution region x ∈ [-\(\frac{9}{2}\), 6]
Note: We know that - 2 < - 1, when remove - ve sign then 2 > 1.

Question 4.
Solve:
- 7 ≤ \(\frac{7-5 x}{4}\) ≤ 10.
Answer:
We have,
- 7 ≤ \(\frac{7-5 x}{4}\) ≤ 10
⇒ - 28 ≤ 7 - 5x ≤ 40
(Multiplying inequality by 4)
⇒ - 28 - 7 ≤ - 7 + 7 - 5x ≤ - 7 + 40
[Adding - 7 in each side)
⇒ - 35 ≤ - 5x ≤ 33
⇒ 7 ≥ x ≥ - \(\frac{33}{5}\)
(Dividing inequality by 5)

Question 5.
Solve the following system of inequality:
4x - 8 < 7 + x .................. (1)
14 - 6x ≤ 2 .................... (2)
and represented graphically on number line.
Answer:
From inequality (I),
4x - 8 < 7 + x
or 4x - x < 7 + 8
or 3x < 15
or x < 5 ....................... (3)
Now from inequality (2),
14 - 6x ≤ 2
- 6x ≤ 2 - 14
or - 6x ≤ - 12
(Dividing both sides by 6)
or - x ≤ - 2
Multiplying by (- 1)
x ≥ 2 ........................... (4)
[Since - 2 < - 1 but 2 > 1]
If we sketch (3) and (4) on number line we sec that common value of x iš equal to or greater than 2 and less than 5 which is shown by dark line in the following figure.

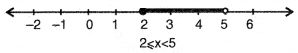
5 > x ≥ 2 is solution of given inequality.
Thus, solution region x ∈ [2, 5)
Here, point S is not included.

Question 6.
Solve the following system of inequality:
4x - 9 ≤ 6 + x ................ (i)
12 - 7x ≤ 5 ........................ (ii)
and represent the solution on number line.
Answer:
Inequality: 4x - 9 ≤ 6 + x
⇒ 4x - x ≤ 6 + 9
⇒ 3x ≤ 15
⇒ x ≤ 5 ....................... (iii)
Then, inequality 12 - 7x ≤ 5
⇒ 12 - 5 ≤ 7x
⇒ 7 ≤ 7x
⇒ 1 ≤ x
⇒ x ≥ 1 .................. (iv)
From equation (iii) and (iv) required solution is x ∈ [1, 5) as shown on number line.
(Point 5 is not included)

Question 7.
In an experiment, a solution of hydrochloric acid is to be kept between 35° and 400 celsius. What is the range of temperature in degree fahrenhiet? If conversion formula is given by C = \(\frac{5}{9}\) (F - 32) where C and F represent temperature in degree celsius and degree fahrenheit respectively.
Answer:
It is given that
35 < C < 40 ............. (1)
Putting formula, C = \(\frac{5}{9}\) (F - 32) in equation (1)
35 < \(\frac{5}{9}\) (F - 32) < 40,
or 9 × 35 < 5 (F - 32) < 40 × 9 (Multiplying by 9)
or 9 × 7 < (F - 32) < 8 × 9 (Dividing by 5)
or 63 < F - 32 < 72
or 63 + 32 < F < 72 + 32
or 95 < F < 104
Thus, required range is from 95° F to 104° F.

Question 8.
In an experiment a solution of hydrochloric acid is to be kept between 25° and 30° celsius. What is the Range of temperature in degree fahrenheit? (f conversion formula is given by C = \(\frac{5}{9}\) (F - 32) where C and F represent temperature in degree celsius and degree fahrenheit respectively.
Answer:
According to question:
25° < C < 30° ........ (i)
and C = \(\frac{5}{9}\) (F - 32) ............... (ii)
From equation (i) and (ii),
25 < \(\frac{5}{9}\) (F - 32) < 30
⇒ \(\frac{9}{5}\) × 25 < F - 32 < \(\frac{9}{5}\) × 30 (Multiplying by \(\frac{9}{5}\))
⇒ 45 < F - 32 < 54
⇒ 45 + 32 < F - 32 + 32 < 54 + 32 (Adding 32 on both sides)
⇒ 77 < F < 86
Thus, the required range of temperature is between 77°F and 86°F.

Question 9.
A manufacturer has 600 litres of a 12% solution of acid. How many litres of a 30% acId solution must be added to it so that acid content in the resulting mixture will be more than 15% but less than 18%.
Answer:
Let x litre of 3o% acid of solution is required to be added, then Total mixture = (x + 600) litres
We have, 30% of x + 12% of 600 > 15% of (x + 600)
and 30%x + 12% of 600 < 18%(x + 600) or \(\frac{30}{100}\)x + \(\frac{12}{100}(\)600) > \(\frac{15}{100}\)(x + 600)
and \(\frac{30}{100}\)x + \(\frac{12}{100}\)(600) < \(\frac{18}{100}\)(x + 600) or 30x + 7200 > 15x + 9000
and 30x + 7200 < 18x + 10800 [Multiplying by 100 in both sides] or 30x - 15x > 9000 - 7200
and 30x - 18x < 10800 - 7200 or 15x > 1800 and 12x < 3600 or x > 120
and x < 300
i.e. 120 < x < 300
Thus, the quantity of litres of the 30% solution of acid will have to be more than 120 litres but less than 300 litres.

Question 10.
Solve the following inequalities:
(i) \(\frac{1}{x-3}\) < 0
Answer:
(i) \(\frac{1}{x-3}\) < 0
⇒ x - 3 < 0 [∵ \(\frac{a}{b}\) < 0 and a > 0 b < 0]
⇒ x < 3
⇒ x ∈ (- ∞, 3)
∴ Solution set of \(\frac{1}{x-3}\) < 0 is (- ∞, 3)

(ii) \(\frac{x+2}{x+3}\) ≥ 2
Answer:

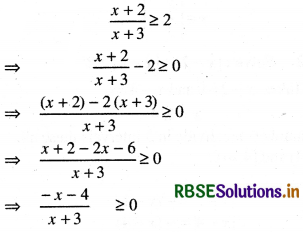
⇒ x ∈ [- 4, - 3)
∴ Solution set of = [- 4, - 3)

Multiple Choice Questions

Question 1.
Solution set of 4x + 3 < 6x + 7 is:
(a) (- 2, ∞)
(b) (2, ∞)
(c) (0, ∞)
(d) (- 2, 8)
Answer:
(a) (- 2, ∞)

Question 2.
If \(\frac{5-2 x}{3}\) ≤ \(\frac{x}{6}\) - 5 then x ∈:
(a) (0, ∞)
(b) (- 2, ∞)
(c) [2, ∞]
(d) [8, ∞)
Answer:
(d) [8, ∞)

Question 3.
Solution of - 8 ≤ 5x - 3 < 7 is:
(a) 1 < x < 3
(b) 0 < x < 3
(c) - 1 ≤ x < 2
(d) 0 ≤ x < 2
Answer:
(c) - 1 ≤ x < 2

Question 4.
The marks obtained by a student of class X in first and second terminal examination are 62 and 48, respectively. Find the minimum marks he should get in the annual examination to have an average of at least 60 marks:
(a) 80
(b) 82
(c) 81
(d) 70
Answer:
(d) 70

Question 5.
If x is a real number then solution set of 5x - 3 < 3x + 1 will be:
(a) x ∈ (0, 2)
(b) x ∈ (- 2, 2)
(c) x ∈ (- ∞, 2)
(d) x ∈ (2, ∞)
Answer:
(c) x ∈ (- ∞, 2)

Question 6.
If x < 5 then:
(a) - x < - 5 (b) - x ≤ - 5 (c) - x > - 5
(d) - x ≥ - 5
Answer:
(c) - x > - 5

Question 7.
If x < y, be b < 0 then:
(a) \(\frac{x}{b}\) < \(\frac{y}{b}\)
(b) \(\frac{x}{b} \leq \frac{y}{b}\)
(c) \(\frac{x}{b}>\frac{y}{b}\)
(d) \(\frac{x}{b} \geq \frac{y}{b}\)
Answer:
(c) \(\frac{x}{b}>\frac{y}{b}\)

Question 8.
If |x - 1| > 5 then:
(a) x ∈ (- 4, 6)
(b) x ∈ (- ∞, - 4) ∪ (6, ∞)
(c) x ∈ [- 4, 6]
(d) x ∈ [- ∞, - 4) ∪ [6,∞)
Answer:
(b) x ∈ (- ∞, - 4) ∪ (6, ∞)

Question 9.
If \(\left|\frac{2}{x-4}\right|\) > 10x ≠ 4 then:
(a) x ∈ (2, ∞)
(b) x ∈ (2, 6)
(c) x ∈ (- ∞, 6)
(d) x ∈ (2, 4) ∪ (4, 6)
Answer:
(d) x ∈ (2, 4) ∪ (4, 6)

Question 10.
If |x - 1| + |x - 2| ≥ 4 then:
(a) x ∈ \(\left[-\frac{1}{2}, \frac{7}{2}\right]\)
(b) x ∈ \(\left(-\infty,-\frac{1}{2}\right] \cup\left[\frac{7}{2}, \infty\right)\)
(c) x ∈ \(\left[-\frac{1}{2}, \frac{3}{2}\right] \cup\left[\frac{5}{2}, \frac{7}{2}\right]\)
(d) None of these
Answer:
(b) x ∈ \(\left(-\infty,-\frac{1}{2}\right] \cup\left[\frac{7}{2}, \infty\right)\)

Fill in the Blanks

Question 1.
If \(\frac{2}{x+2}\) > 0, then x .........................
Answer:
x > - 2

Question 2.
If - 4x ≥ 12, then x .................. - 3
Answer:
x ≤ - 3

Question 3.
If |x - 1| ≤ 2, then - 1 ........ x ........ 3
Answer:
- 1 ≤ x ≤ 3

Question 4.
If p > 0, q > 0, then p + q .............................. p
Answer:
> p

Question 5.
If x > y and b < 0, then bx ........... by.
Answer:
bx < by

Question 6.
If x + 5 < 0, then x < .............................
Answer:
x < - 5 Question 7. If |x| = 0, then x = ...........................
Answer:
x = 0

State which of the following statement is True/False.

Question 1.
If |x| ≤ 5, then x ∈ [- 5, 5].
Answer:
True

Question 2.
If xy > 0, then x < 0 and y < 0
Answer:
True

Question 3.
If xy < 0, then x < 0 and y < 0
Answer:
False

Question 4.
If x > 5 and x > 2, then x ∈ (5, ∞)
Answer:
True

Question 5.
If x + 5 > 3, then x = - 2
Answer:
False

Question 6.
|x + 5| ≤ 2, then x ∈ [- 7, - 3]
Answer:
True

Question 7.
If x > 0, then |x - 7| ≥ 0.
Answer:
True