RBSE Class 11 Maths Important Questions Chapter 5 Complex Numbers and Quadratic Equations

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 5 Complex Numbers and Quadratic Equations Questions and Answers.

RBSE Class 11 Maths Chapter 5 Important Questions Complex Numbers and Quadratic Equations

Question 1.
Find conjugate of \(\frac{(4-3 i)(3+4 i)}{(1+3 i)(3-i)}\).
Answer:
Here,

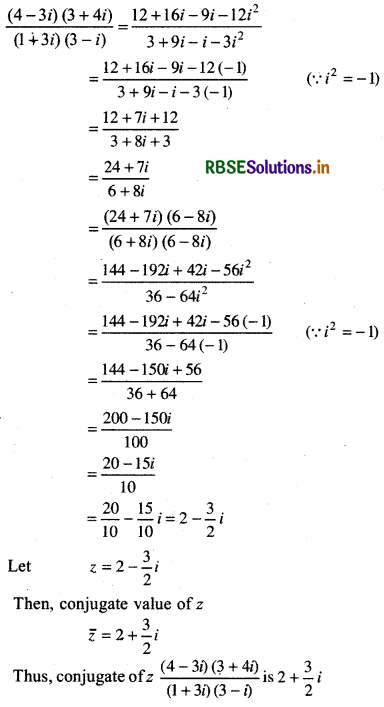
Question 2.
Find conjugate of \(\frac{(3-2 i)(2+3 i)}{(1+2 i)(2-i)}\).
Answer:
Here,

Question 3.
Find modulus and argument of the following complex numbers:
(i) i
(ii) 1 - i
Answer:
(i) Le z = i = r(cos θ + i sin θ)
Comparing real and imaginary parts on both sides
or 0 + i = r(cos θ + i sin θ)
r cos θ = 0
and r sin θ = 1
Squaring and adding,
r² cos²θ + r² sin² θ = 1
or r² = 1 (∵ sin² θ + cos² θ = 1)
or r = 1
Now, cos θ = 0 and sin θ = \(\frac{1}{1}\) = 1
or θ = \(\frac{\pi}{2}\) or θ = \(\frac{\pi}{2}\)
Thus, θ = \(\frac{\pi}{2} \)Thus, modulus of i, is 1 and argument \(\frac{\pi}{2}\).

(ii) Let z = 1 - i = r (cos θ + i sin θ)
Comparing real and imaginary values of on both sides
r cos θ = 1, r sin θ = - 1
Squaring and adding,
r² cos² θ + r² sin² θ = 1 + 1 = 2
or r² (cos² θ + sin² θ) = 2
or r² = 2 [∵ cos² θ + sin² θ = 1]
or r = √2
∵ cos θ = \(\frac{1}{\sqrt{2}}\) and sin θ = - \(\frac{1}{\sqrt{2}}\)
or θ = - \(\frac{\pi}{4}\)
Thus, modulus of 1 - i is √2 and argument -\(\frac{\pi}{4}\).

Question 4.
If \(\frac{2+2 i \cos \theta}{1-2 i \cos \theta}\) is real then find real value of θ.
Answer:

Question 5.
If x + iy = \(\frac{a+i b}{a-i b}\) then prove that x² + y² = 1.
Answer:

Question 6.
Write polar form of complex number
z = \(\frac{i+1}{\cos \frac{\pi}{6}+i \sin \frac{\pi}{6}}\).
Answer:

Question 7.
If z₁ and z₂ are two complex numbers that |z₁ + z₂| = |z₁ - z₂|, then prove that:
Argument (z₁) - Argument (z₂) = \(\frac{\pi}{2}\)
Answer:
Let z₁ = r₁ (cos θ₁ + i sin θ₁)
and z₂ = r₂ (cos θ₂ + i sin θ₂)
then z₁ + z₂ = (r₁ cos θ₁ + r₂ cos θ₂) + i(r₁ sin θ₁ + r₂ sin θ₂)
and z₁ - z₂ = (r₁ cos θ₁ - r₂ cos θ₂) + i(r₁ sin θ₁ - r₂ sin θ₂)
|z₁ + z₂|² = [(r₁ cos θ₁ + r₂ cos θ₂)² + (r₁ sin θ₁ + r₂ sin θ₂)²]
= r₁² cos² θ₁ + r₂² cos² θ₂ + 2 r₁r₂ cos θ₁ cos θ₂ + r₁² sin² θ₁ + r₂² sin² θ₂ + 2r₁r₂ sin θ₁ sin θ₂
= r₁² + r₂² + 2r₁ r₂ cos (θ₁ - θ₂) (∵ sin²θ + cos²θ = 1)
and |z₁ - z₂|² = ((r₁ cos θ₁ - r₂ cos θ₂)² + (r₁ sin θ₁ - r₂ sin θ₂)²]
= r₁² cos² θ₁ + r₂² cos² θ₂ - 2r₁r₂ cos θ₁ cos θ₂ + r₁² sin² θ₁ + r₂² sin² θ₂ - 2r₁r₂ sin θ₁ sin θ₂
= r₁² + r₂ - 2r₁r₂ cos (θ₁ - θ₂)2 cos (θ₁ - θ₂)
∵ |z₁ + z₂|² = |z₁ - z₂|²
⇒ r₁² + r₂² + 2r₁r₂ cos(θ₁ - θ₂)
⇒ r₁² + r₂² - 2r₁r₂ cos (θ₁ - θ₂)
⇒ 4r₁r² cos(θ₁ - θ₂) = 0
⇒ cos(θ₁ - θ₂) = 0 (∵r₁r₂ = 0)
⇒ θ₁ - θ₂ = \(\frac{\pi}{2}\)
⇒ Argumentz₁ - Argumentz₂ = \(\frac{\pi}{2}\) Hence Proved.

Question 8.
Find multiplicative inverse of complex number 3 + 2i.
Answer:
Let 3 + 2i is multiplicative inverse of x + iy
then (3 + 2i)(x + iy) = 1 = 1 + oi
or (3x - 2y) + i(2x + 3y) = 1 + 0.i
On comparing on both sides,
3x - 2y = 1
and 2x + 3y = 0
∴ x = \(\frac{3}{13}\), y = \(\frac{2}{13}\)
∴ Multiplicative inverse of 3 + 2i = \(\frac{3}{13}-\frac{2}{13}\) i

Multiple choice Questions

Question 1.
i + \(\frac{1}{i}\) equals:
(a) 0
(b) - 1
(c) 1
(d) None of these
Answer:
(a) 0

Question 2.
i^-101 equals:
(a) - i
(b) 4
(c) - 1
(d) None of these
Answer:
(a) - i

Question 3.
\(\frac{1}{(1-i)^2}-\frac{1}{(1+i)^2}\) equals:
(a) - i
(b) i
(c) 1
(d) None of these
Answer:
(b) i

Question 4.
(1 + i) (1 + i²) + (1 + i³) (1 + i⁴) (1 + i⁵)equals:
(a) 1
(b) - 1
(c) 4
(d) None of these
Answer:
(c) 4

Question 5.
If \(\frac{2+3 i \sin \theta}{1-3 i \sin \theta}\) is a real number and 0 < θ < 2π, then θ =
(a) π
(b) \(\frac{\pi}{2}\)
(c) \(\frac{3 \pi}{2}\)
(d) None of these
Answer:
(a) π

Question 6.
If x is real then satisfy \(\frac{1-i x}{1+i x}\) = a - ib, then a² + b² equals:
(a) - 1
(b) 1
(c) 0
(d) None of these
Answer:
(b) 1

Question 7.
If x + iy = \(\sqrt{\frac{a+i b}{c+i d}}\), then value of (x² + y²)² is:
(a) \(\frac{c^2+d^2}{a^2+b^2}\)
(b) \(\frac{a^2+b^2}{c^2+d^2}\)
(c) \(\frac{a^2-b^2}{a^2-d^2}\)
(d) None of these
Answer:
(b) \(\frac{a^2+b^2}{c^2+d^2}\)

Question 8.
Modulus of complex number i is:
(a) 1
(b) 0
(c) \(\frac{1}{2}\)
(d) None of these
Answer:
(a) 1

Question 9.
Argument of - 1 + i is:
(a) 135°
(b) 150°
(c) 270°
(d) None of these
Answer:
(a) 135°

Question 10.
Modulus of (2 + 3i)² is:
(a) 13
(b) 15
(c) 12
(d) None of these
Answer:
(a) 13

Question 11.
If x + iy = (1 + i) (1 + 2i) (1 + 3i) then x² + y² equals:
(a) 0
(b) 1
(c) 100
(d) None of these
Answer:
(c) 100

Question 12.
If z = \(\frac{1}{1-\cos \theta-i \sin \theta}\) then Re (z)equals:
(a) 0
(b) \(\frac{1}{2}\)
(c) tan \(\frac{\theta}{2}\)
(d) None of these
Answer:
(b) \(\frac{1}{2}\)

Question 13.
If θ is argument of \(\frac{3+2 i}{3-2 i}\), then tan θ equals:
(a) \(\frac{6}{13}\)
(b) \(\frac{12}{5}\)
(c) \(\frac{5}{13}\)
(d) None of these
Answer:
(b) \(\frac{12}{5}\)

Question 14.
If a = 1 + i, then a² equals:
(a) (1 - i)
(b) 2i
(c) (1 + i) (1 - i)
(d) None of these
Answer:
(b) 2i

Question 15
Principal argument of (1 + i) is:
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{6}\)
(c) \(\frac{3 \pi}{4}\)
(d) None of these
Answer:
(a) \(\frac{\pi}{4}\)

Question 16.
If z = x + iy, then real part of \(\frac{1}{z-1}\) is:
(a) \(\frac{x-1}{x^2+y^2-2 x+1}\)
(b) \(\frac{x+1}{x^2+y^2-2 x+1}\)
(c) \(\frac{x-1}{x^2-y^2+2 x+1}\)
(d) None of these
Answer:
(a) \(\frac{x-1}{x^2+y^2-2 x+1}\)

Question 17.
1 + i² + i⁴ + i⁶ equals:
(a) 0
(b) 1
(c) - 1
(d) None of these
Answer:
(a) 0

Question 18.
i¹⁰⁸ + i¹¹⁷ + i¹¹⁰ + i¹¹⁵ equals:
(a) - 1
(b) 0
(c) 1
(d) None of these
Answer:
(b) 0

Question 19.
1 + i¹⁰ + i¹⁰⁰ - i¹⁰⁰ equals:
(a) 1
(b) 0
(c) - 1
(d) None of these
Answer:
(c) - 1

Question 20.
(1 + i)⁴ (1 + \(\frac{1}{i}\))⁴ equals:
(a) 16
(b) - 16
(c) 8
(d) None of these
Answer:
(a) 16

Question 21.
Multiplicative inverse of 2 + 3i is:
(a) \(\frac{2}{13}-\frac{3 i}{13}\)
(b) \(\frac{2}{13}+\frac{3 i}{13} \)
(c) -\(\frac{2}{13}-\frac{3 i}{13}\)
(d) None of these
Answer:
(a) \(\frac{2}{13}-\frac{3 i}{13}\)

Question 22.
Multiplicative inverse of \(\frac{(i+1)(i+2)}{(i-1)(i-2)}\) is:
(a) \(\frac{-4}{5}-\frac{3}{5}\) i
(b) \(\frac{4}{5} i+\frac{3}{5}\) i
(c) \(\frac{4}{5} i-\frac{3}{5} i\)
(d) None of these
Answer:
(a) \(\frac{-4}{5}-\frac{3}{5} i\)

Question 23.
For complex number z, \(\overline{(\bar{z})}\) equals:
(a) z̅
(b) z
(c) |z|²
(d) None of these
Answer:
(b) z

Question 24.
For complex number z, zz̅ equals:
(a) |z|²
(b) |z|
(c) \(\left|\frac{1}{z}\right|^2\)
(d) None of these
Answer:
(a) |z|²

Question 25.
Conjugate of 5 + 12i is:
(a) - 5 + 12i
(b) 5 - 12i
(c) - 5 - 12i
(d) None of these
Answer:
(b) 5 - 12i

Question 26.
If z̅ = z then z:
(a) Purely real
(b) Purely imaginary
(c) Neither real nor imaginary.
(d) None of the above
Answer:
(a) Purely real

Question 27.
If z̅ = - z, then z:
(a) Purely imaginary
(b) Purely real
(c) Both real and imaginary
(d) None of these
Answer:
(a) Purely imaginary

Question 28.
For any complex number z, z + z̅:
(a) Real
(b) imaginary
(c) Both (a) and (b)
(d) None of these
Answer:
(a) Real

Question 29.
If a + ib = \(\sqrt{\frac{1+i}{1-i}}\) then a² + b² equals:
(a) 1
(b) - 1
(c) 0
(d) None of these
Answer:
(a) 1

Question 30.
If a = 3 + 2i then a⁴ - 12a³ + 62a² - 156a equals:
(a) - 169
(b) 169
(c) 0
(d) None of these
Answer:
(a) - 169

Question 31.
Principal argument of (cos \(\frac{\pi}{6}\) + i sin \(\frac{\pi}{6}\))
(a) \(\frac{\pi}{6}\)
(b) \(\frac{\pi}{4}\)
(c) \(\frac{\pi}{3}\)
(d) None of these
Answer:
(a) \(\frac{\pi}{6}\)

Question 32.
\(\left|\frac{1+\cos \theta+i \sin \theta}{1+\cos \theta-i \sin \theta}\right|\) equals:
(a) 1
(b) 2
(c) \(\frac{1}{2}\)
(d) None of these
Answer:
(a) 1

Question 33.
If (x + iy) = \(\frac{(a+i)^2}{2 a-i}\), then x² + y² equals:
(a) \(\frac{\left(a^2+1\right)^2}{4 a^2+1}\)
(b) \(\frac{\left(a^2-1\right)^2}{4 a^2+1}\)
(c) \(\frac{\left(a^2+1\right)^2}{4 a^2-1}\)
(d) None of these
Answer:
(a) \(\frac{\left(a^2+1\right)^2}{4 a^2+1}\)

Question 34.
If complex numbers z₁, z₂ and z₃ are verticies of an equilateral triangle, then z₁ + z₂ + z₃ equals:
(a) 0
(b) 1
(c) - 1
(d) None of these
Answer:
(a) 0

Question 35.
Polar form of (1 + i) is:
(a) \(\frac{1}{\sqrt{2}}\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)\)
(b) \(\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)\)
(c) \(\left(\cos \frac{\pi}{4}-i \sin \frac{\pi}{4}\right)\)
(d) None of these
Answer:
(d) None of these

Question 36.
Polar form of 3 + 4i is:
(a) \(\cos \left(\tan ^{-1} \frac{4}{3}\right)+i \sin \left(\tan ^{-1} \frac{4}{3}\right)\)
(b) 5\(\left[\cos ^{-1}\left(\frac{4}{3}\right)+i \sin ^{-1}\left(\frac{4}{3}\right)\right]\)
(c) \(\cos \left(\tan ^{-1} \frac{4}{3}\right)-i \sin \left(\tan ^{-1} \frac{4}{3}\right)\)
(d) None of the above
Answer:
(d) None of the above

Fill in the Blanks

Question 1.
The conjugate of complex number z = 3 - i is ................................
Answer:
3 + i

Question 2.
If (2 + i) (2 + 2i) (2 + 3i) ....... (2 + ni) = x + iy, then 5.8.13 ...................... (4 + n²) = ...........................
Answer:
x² + y²

Question 3.
If |z| = 5 and arg(z) = \(\frac{\pi}{4}\) then z = .....................................
Answer:
z = 5\(\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)\)

Question 4.
The value of i¹¹¹ + 2i²⁹ - \(\frac{3}{i^{99}}\) is ..............................
Answer:
- 2i

Question 5.
For any complex number z = 3 + 4i the multiplicative inverse is ...............................
Answer:
\(\frac{3-4 i}{25}\)

Question 6.
Principal arg(z) is lie ............................
Answer:
- π < θ ≤ π.

Question 7.
The roots of equation x² + 4 = 0 are ..................................
Answer:
± 2i

Question 8.
arg\(\left(\frac{z_1}{z_2}\right)\) = ........................................
Answer:
arg(z₁) - arg(z₂)

Question 9.
If arg of z - 2 - 3i is π/4 than locus of z is ........................................
Answer:
Straight line

True/False

Question 1.
The modulus of z = 3 - i is 10.
Answer:
True

Question 2.
The conjugate of 5 + 3i is 5 - 3i
Answer:
True

Question 3.
The polar form of 1 - i is √2 (cos \(\frac{\pi}{4}\) + i sin \(\frac{\pi}{4}\))
Answer:
False

Question 4.
For any complex number z is
z̄ = \(\frac{1}{z}\)
Answer:
False

Question 5.
If z = 4 +3i then its multiplicative inverse is 4 - 3i.
Answer:
False

Question 6.
If z + z̄ = 0 then z is purelyded.
Answer:
False

Question 7.
If a + ib = \(\sqrt{\frac{x+i}{x-i}}\) then a² + b² = 1.
Answer:
True

Question 8.
For an two complex number z₁ and z₂, z₁ + z₂ = z₂ + z₁.
Answer:
True

Question 9.
If z = √3 + i the arg(z) = π/6.
Answer:
True