RBSE Class 11 Maths Important Questions Chapter 4 गणितीय आगमन का सिद्धांत

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 4 गणितीय आगमन का सिद्धांत Important Questions and Answers.

RBSE Class 11 Maths Chapter 4 Important Questions गणितीय आगमन का सिद्धांत

अतिलघूतरात्मक प्रश्न- 

प्रश्न 1.
यदि कथन P(n): n³ + 2, 5 का गुणज है । क्या यह कथन n .के सभी मानों के लिए सत्य है?
हल:
असत्य है। ∵ n∈ N के लिए यह 5 का गुणज प्राप्त नहीं होता है|

प्रश्न 2.
यदि कथन P (n) है "n² - n + 41 अभाज्य संख्या है" तो P( 41 ) का मान लिखिए।
हल:
P(41) = (41)² – 41 + 41 = (41)²
जो कि अभाज्य संख्या नहीं है। अतः कथन असत्य है

प्रश्न 3.
2 + 4 + 6 + ................. n पदों का योग लिखिए।
हल:

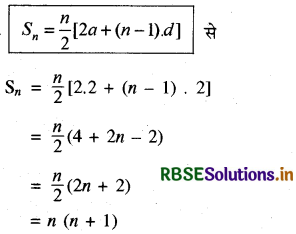
प्रश्न 4.
यदि P(n) कथन है "n² + n सम संख्या है।" तो P( 3 ) का मान लिखिए।
हल:
P (3) = (3)² + 3 = 9 + 3 = 12
जो कि एक सम संख्या है।

प्रश्न 5.
n ∈ N के लिए 2³ⁿ - 7n - 1, जहाँ n एक धनपूर्णांक है, किससे विभाज्य है? लिखिए ।
हल:
49 से। ∵ n = 2 रखने पर 49 प्राप्त होता है।

प्रश्न 6.
3²ⁿ - 2n - 1, ∀ n ∈ N को विभाजित करने वाला सबसे बड़ा धनात्मक पूर्णांक लिखिए।
हल:
माना T_n = 3²ⁿ – 2n - 1
या T_n = 3²ⁿ - (2n + 1)
यहाँ हम देखते हैं कि 3²ⁿ तथा (2n + 1), n के प्रत्येक मान के लिए विषम हैं। लेकिन प्रत्येक दो विषम संख्याओं का अन्तर हमेशा सम होता है और सभी सम संख्याएँ 2 से विभाज्य होती हैं। ∴ 3²ⁿ - 2n - 1 ∀ n ∈ N को विभाजित करने वाला सबसे बड़ा धनात्मक पूर्णांक 2 होगा।

प्रश्न 7.
यदि n सम प्राकृत संख्या हो, तो n (2 1) को विभाजित करने वाला सबसे बड़ा धनात्मक पूर्णांक लिखिए ।
हल:
माना T_n = n(n² - 1) = n(n - 1) (n + 1)
या T_n = (n - 1) n (n + 1)
यहाँ हम देखते हैं कि n (n² - 1 ) क्रमश: तीन प्राकृत संख्याओं (n - 1) n (n + 1) का गुणनफल है। इन तीनों संख्याओं में से पहली विषम संख्या, दूसरी सम संख्या तथा तीसरी 3 का गुणक है । अत: n (n² - 1 ) को विभाजित करने वाला सबसे बड़ा धनात्मक पूर्णांक 6 है।

प्रश्न 8.
यदि कथनं P (n) : n (n + 1) + 1 है, तो P(4) लिखिए।
हल:
∵ P (n) = n(n + 1) + 1
∴ P(4) = 4(4 + 1) + 1
= 4.5+ 1
= 20 + 1
= 21

प्रश्न 9.
यदि कथन P (n) : 4ⁿ > n है, तो क्या P(3) सत्य है ?
हल:
∵ P(n) : 4ⁿ > n
∴ P(3) : 4³ > 3
64 > 3
अतः यह कथन सत्य है|

प्रश्न 10.
यदि कथन P(n) : n(n + 1) + 1 विषम संख्या है, तो P(3) लिखिए।
हल:
P( 3 ) = 3(3 + 1) + 1
= 3 × 4 + 1
P(3) = 13

प्रश्न 11.
यदि कथन P(n) : n³ + 2, 5 का गुणज है। क्या कथन " के सभी मानों के लिए सत्य है ?
हल:
असत्य है।

प्रश्न 12.
1 + (1 + 3) + (1 + 3 + 5) + ........................ का nवाँ पद लिखिए।
हल:
T_n = 1 + 3+ 5 + 7 + .......................... nपद

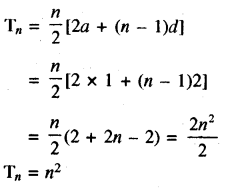
T_n = n²

प्रश्न 13.
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\ldots \ldots+\frac{1}{n(n+1)}\) का योग लिखिए|
हल:
माना इनका योग T_n है ।

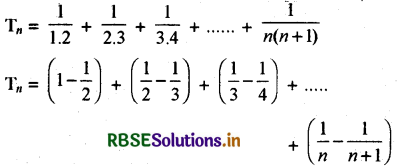
अतः यह स्पष्ट है कि यहाँ पर संख्याएँ आपस में मिलकर कट रही हैं, केवल शेष निम्न संख्याएँ ही बचेंगी-
T_n = 1 - \(\frac{1}{n+1}\)
= \(\frac{n+1-1}{n+1}\) = \(\frac{n}{n+1}\)

प्रश्न 14.
यदि कथन P (n) : n (n + 1) (n + 2), "12 से भाज्य' तो प्रदर्शित कीजिए कि P (3) व P(4) सत्य हैं लेकिन P(5) नहीं ।
हल:
P(n): n(n + 1) (n + 2), 12 सें भाज्य है।
n = 3 के लिए P( 3 ) : 3(3 + 1) (3 + 2) = 3 × 4 × 5 = 12 × 5
जो कि 12 से भाज्य है। अत: P (3) सत्य है।
n = 4 के लिए P (4): 4(4 + 1) (4 + 2) = 4 × 5 × 6 = 120 = 12 × 10
जो कि 12 से भाज्य है। अत: P( 4 ) सत्य है।
n = 5 के लिए P (5): 5 (5 + 1) (5 + 2) = 5 × 6 × 7 = 210
जो कि 12 से भाज्य नहीं है । अत: P ( 5 ) सत्य नहीं है।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
गणितीय आगमन सिद्धान्त के द्वारा सिद्ध कीजिए कि प्रत्येक प्राकृतिक संख्या n के लिए
2 + 2² + 2³ + ................ + 2ⁿ = 2.(2ⁿ - 1)
हल:
दिए गए सूत्र के दोनों पक्षों में n = 1 रखने पर
वामपक्ष = 2¹ = 2 तथा दक्षिणपक्ष = 2(2¹ - 1) = 2
∴ दिया गया सूत्र n = 1 के लिए सत्य है।
पुनः माना कि दिया गया सूत्र के n = k के लिए सत्य है ।
∴ सूत्र में n = k रखने पर
2 + 2² + 2³ + .................... + 2^k = 2(2^k - 1) .................... (i)
अब सूत्र के वामपक्ष में दी गई श्रेणी के भवें पद 2ⁿ में n = k + 1 रखने पर 2^{k + 1} प्राप्त होता है जिसे समीकरण (i) के दोनों पक्षों में जोड़ने पर
2 + 2² + 2³ + ..................... + 2^k + 2^{k + 1} = 2(2^k - 1) + 2^{k + 1}
= 2^{k + 1} - 2 + 2^{k + 1}
= 2.2^{k + 1} - 2
= 2 (2^{k + 1} - 1)
इससे प्रदर्शित होता है कि दिया हुआ सूत्र n = k + 1 के लिए भी सत्य है। अतः गणितीय आगमन सिद्धान्त से दिया हुआ सूत्र प्रत्येक n ∈ N के लिए सत्य है।

प्रश्न 2.
गणितीय आगमन सिद्धान्त द्वारा सिद्ध कीजिए कि प्रत्येक प्राकृतिक संख्या n के लिए 11^{n + 2} + 12^{2n + 1}, 133 से विभाज्य है।
हल:
दोनों पक्षों में n = 1 रखने पर
11^{n + 2} + 12^{2n + 1} = 11³ + 12³ = 1331 + 1728 = 3059
= 133 × 23
जो कि स्पष्टत: 133 से विभाज्य है ।
∴ दिया हुआ कथन n = 1 के लिए सत्य है।
माना कि दिया हुआ कथन n = k के लिए सत्य है।
अर्थात् (11)^{k + 2} + 12^{2k + 1}, 133 से विभाज्य है ।
∴ (11)^{k + 2} + 12^{2k + 1} = 133p [जहाँ p ∈ N] ......... (i)
पुन: n = k + 1 लेने पर
11^{n + 2} + 12^{2n + 1} = 11^{k + 3} + 12^{2k + 3}
= 11. 11^{k + 2} + 12², 12^{2k + 1}
= 11. 11^{k + 2} + 144, 12^{2k + 1}
= 11. 11^{k + 2} + (11 + 133). 12^{2k + 1}
= 11. (11^{k + 2} + 12^{2k + 1}) + 133 . 12^{2k + 1}
= 11. (133p) + 133. 12^{2k + 1} [समीकरण (i) से]
= 133 (11p + 12^{2k + 1})
स्पष्ट है कि दायाँ पक्ष 133 से विभाज्य है ।
इससे प्रदर्शित होता है कि n = k + 1 के लिए भी 11^{n + 2} + 12^{2n + 1}, 133 से विभाज्य है। अतः गणितीय आगमन सिद्धान्त से दिया हुआ कथन प्रत्येक n ∈ N के लिए सत्य है।

प्रश्न 3.
गणितीय आगमन सिद्धान्त के द्वारा सिद्ध कीजिए कि n ≥ 3, n ∈ N के लिए 2ⁿ > 2n + 1
हल:
हम देखते हैं कि n = 1 के लिए 2¹ ≯ 2.1 + 1 = 3
तथा n = 2 के लिए 2² ≯ 2.2 + 1 = 5
और n = 3 के लिए 2³ = 8 तथा 2.3 + 1 = 7
अर्थात् 2³ > 2.3 + 1
अतः दिया गया कथन n = 3 के लिए सत्य है।
माना दिया गया कथन n = k के लिए सत्य है, जहाँ k > 3
अर्थात्_ n = k के लिए
2^k > 2^{k + 1} ................ (i)
अब n = k + 1 के लिए
2ⁿ = 2^{k + 1} = 2¹ . 2^k = 2.2^k
> 2(2k + 1) [समीकरण (i) से]
> 2(k + k + 1)
> 2(k + 1) + 2k
> 2(k + 1) + 1 [∵ k > 3 ⇒ 2k > 6 > 1]
अर्थात् 2^{k + 1} > 2 (k + 1) + 1
अतः दिया गया कथन n = k + 1 के लिए भी सत्य है।
∴ गणितीय आगमन सिद्धान्त से दिया गया कथन प्रत्येक n ≥ 3, n ∈ N के लिए सत्य है।

प्रश्न 4.
1 + 3 + 5 + ......... + (2n - 1) = n²
हल:
P (n): 1 + 3 + 5 + ................. + (2n - 1) = n²
P( 1 ) के लिए n = 1 रखने पर L.H.S. = 1 L.H.S. = 1
R.H.S. = 1² = 1
∴ L.H.S. = R.H.S.
P(2) के लिए n = 2 रखने पर L.H.S. = 1 + 3: = 4
R.H.S.= 2² = 4
∴ L.H.S. = R.H.S.
अतः कथन P(1) तथा P ( 2 ) सत्य हैं ।
माना कि कथन P(k) सत्य है, अर्थात्
1 + 3 + 5 + ................... (2k - 1) = k² ................... (i)
P(k + 1 ) के लिए दोनों पक्षों में 2 (k + 1 ) - 1 = 2(k + 1) जोड़ने पर
1 + 3 + 5 + (2k - 1) + (2k + 1) = k² + (2k + 1)
[समीकरण (i) से मान रखने पर ]
= (k + 1)²
कथन P(k + 1), कथन P(k) P(k + 1) के रूप में है अर्थात् कथन p(k + 1) सत्य है। अर्थात् कथन n के सभी मानों के लिए सत्य है।

प्रश्न 5.
3²ⁿ - 1, 8 से भाज्य है ।
हल:
कथन P (n): 3²ⁿ - 1, 8 से भाज्य है
अर्थात् 3²ⁿ - 1 = 8d
P(1) के लिए n = 1 रखने पर
3^2.1 - 1 = 8, 8 से भाज्य है ।
P(2) के लिए n = 2 रखने पर
3^2.2 - 1 = 81 - 1 = 80, 8 से भाज्य है।
अत: P(1) तथा P(2) सत्य हैं ।
माना कि कथन P(k) सत्य है, अर्थात्
3^2k - 1 = 8d ............... (i)
कथन P(k + 1) की सत्यता की जाँच के लिए
= 3^{2(k + 1)} - 1
= 3^{2k + 2} - 1
= 3^2k 3². 1
= (8d + 1)3² - 1 [समीकरण (i) से मान रखने पर]
= (8d + 1) . 9 - 1
= 9.8d + 9 - 1
= 9.8d + 8
= 8 (9d + 1) = 8L L ∈ I
अत: 3^2(k+1) - 1, 8 से भाज्य है।
⇒ P(k + 1) सत्य कथन है
अत: कथन P(n), n के प्रत्येक मान के लिए सत्य है।

प्रश्न 6.
7²ⁿ + 2^{3n - 3} . 3^{n - 1}, 25 से भाज्य है ।
हल:
P(n) : 7²ⁿ + 2^{3n - 3} . 3^{n - 1}, 25
अर्थात् 7²ⁿ + 2^{3n - 3} . 3^{n - 1} = 25d
P(1) के लिए n = 1 रखने पर
7^2.1 + 2^3-3 . 3^{1 - 1} = 49 + 1 = 50, 25 से भाज्य है ।
P(2) के लिए n = 2 रखने पर -
7^{2 × 2} + 2^{3 × 2 - 3} × 3^{2 - 1} = 7⁴ + 2³ × 3 = 2401 + 24
= 2425, 25 से भाज्य है।
अतः कथन P(1) तथा P (2) सत्य हैं ।
माना कि कथन P(k) सत्य है। अर्थात्
7^2k + 2^{3k - 3} . 3^{k - 1} = 25d ................. (i)
P(k + 1) की सत्यता की जाँच के लिए
7^{2(k + 1)} + 2^{3(k + 1) - 3} - 3^{k + 1 - 1}
= 7^2k. 7² + 2^3k . 3^k
= (25d - 2^{3k - 3} . 3^{k - 1}) 49 + 2^3k . 3^k [समीकरण (i) से मान रखने पर]
= 25d . 49 - 49.2^{3k - 3} . 3^{k - 1} + 2^3k . 3^k
= 25d. 49 - 2^{3k - 3}. 3^{k - 1} (49 - 2³ . 3¹)
= 25d. 49 - 2^{3k - 3} . 3^{k - 1} . 25
= 25 [49d - 2^{3k - 3} . 3^{k - 1}]
= 25L जहाँ L ∈ I
⇒ 7^{2(k + 1)} + 2^{3(k + 1)- 3} . 3^{(k + 1) - 1, 25} से भाज्य है।
⇒ P(k + 1) सत्य है ।
इससे सिद्ध होता है कि P (n), n के प्रत्येक मान के लिए सत्य है।

प्रश्न 7.
n(n + 1) (n + 2), 6 से भाज्य है ।
हल:
कथन P (n) : n (n + 1) (n + 2), 6 से भाज्य है।
कथन P( 1 ) के लिए, 1(1 + 1) (1 + 2) = 6, 6 से भाज्य है।
कथन P( 2 ) के लिए, 2 ( 2 + 1) (2 + 2) = 24, 6 से भाज्य है।
अतः कथन P(1) तथा P (2) सत्य हैं।
माना कि कथन P (k) सत्य है, अर्थात्
k(k + 1) (k + 2), 6 से भाज्य है ।
⇒ k(k + 1) (k + 2) = 6d, d (पूर्णांक है)
कथन P(k + 1) के लिए-
(k + 1) (k + 2) (k + 3) = k (k + 1) (k + 2) + 3(k + 1) (k + 2)
= 6d + 3(k + 1) (k + 2)
(k + 1) तथा (k + 2) दो क्रमागत संख्याएँ हैं।
जिनका गुणनफल सदैव सम संख्या होती है। अत: 3 (k + 1)
(k + 2) भी 6 से भाज्य होगी।
अर्थात् (k + 1) (k + 2) (k + 3) भी 6 से भाज्य होगी।
अतः कथन P(k + 1) सत्य है
अत: कथन P(n), n के सभी मान के लिए सत्य है|

प्रश्न 8.
गणितीय आगमन सिद्धान्त के प्रयोग द्वारा प्राकृत संख्याओं (n ∈ N) के लिए सिद्ध कीजिए कि
1³ + 2³ + 3³ + ........ + n³ = \(\frac{[n(n+1)]^2}{4}\) = \(\frac{n^2(n+1)^2}{4}\)
हल:
माना कि
P(n) : 1³ + 2³ + 3³ + ........ + n³ = \(\frac{[n(n+1)]^2}{4}\)
n = 1 रखने पर
L.H.S.
= P(1) = 1³ = 1
R.H.S. = \(\frac{[1(1+1)]^2}{4}=\frac{4}{4}\) = 1
L.H.S. = R.H.S.
अतः कथन n = 1 के लिए सत्य है।
पुनः माना कि कथन n = k अर्थात् P(k) सत्य है।

अतः कथन P(k + 1) के लिए सत्य है ।
अतः गणितीय आगमन सिद्धान्त से दिया गया कथन सभी प्राकृत संख्याओं ņ के लिए P(n) सत्य है।

निबन्धात्मक प्रश्न-

प्रश्न 1.
गणितीय आगमन विधि से सिद्ध कीजिए कि n(n + 1) (2n + 1), 6 से विभाजित है
∀ n ∈ N.
हल:
माना P(n) कथन है-
“n(n + 1) (2n + 1), 6 से विभाजित है। "
⇒ P(n) : n(n + 1) (2n + 1), 6 से विभाजित है।
यहाँ P(n) : n(n + 1) (2 × 1 + 1), 6 से विभाजित है।
n = 1 रखने पर
∵ 1(1 + 1) (2n + 1) = 6, जो कि स्पष्टतया 6 से विभाजित है ।
∴ P (1) सत्य कथन है ।
माना P(k) सत्य कथन है ।
तब k(k + 1) (2k + 1), 6 से विभाजित है।
⇒ k(k + 1) (2k + 1) = 6d ∀ d ∈ N ........ (i)
अब हम सिद्ध करेंगे कि P (k + 1) सत्य है और इसके लिए हम सिद्ध करेंगे कि (k + 1) (k + 1 + 1) [2(k + 1) + 1], 6 से विभाजित है।
यहाँ (k + 1) (k + 1 + 1) [2(k + 1) + 1]
= (k + 1) (k + 2) (2k + 2 + 1)
= (k + 1) (k + 2) (2k + 1 + 2)
= (k + 1) (k + 2) (2k + 1) + 2(k + 1) (k + 2)
= k(k + 1) (2k + 1) + 2(k + 1) (2k + 1) + 2(k + 1) (k + 2)
= k(k + 1) (2k + 1) + 2(k + 1) (2k + 1 + k + 2)
= k(k + 1) (2k + 1) + 2(k + 1) (3k + 3)
= k(k + 1) (2k + 1) + 6(k + 1)²
= 6d + 6(k + 1)² [समीकरण (i) के प्रयोग से]
= 6[d + (k + 1)²] = 6L
जहाँ L = d + (k + 1)² ∈ N, जो कि 6 से विभाजित है ।
⇒ P(k + 1) सत्य कथन है ।
अत: P(k) सत्य है ⇒ P (k + 1) सत्य है ।
अतः गणितीय आगमन विधि से दिया हुआ कथन सत्य कथन है ∀ n ∈ N.

प्रश्न 2.
5 + 55 + 555 + ......... + 555 .......... 5 (n अंक) = \(\frac{5}{81}\) (10^{n + 1} - 9n - 10)
हल:

कथन P(k + 1), कथन P (k) के समान है, इसलिए कथन P(k + 1) भी प्रत्येक मान के लिए सत्य होगा।

प्रश्न 3.
आगमन विधि से सिद्ध करें
cos α + cos 2α + ..... + cos nα = sin \(\frac{n \alpha}{2}\) cosec \(\frac{\alpha}{2}\) cos \(\frac{(n+1) \alpha}{2}\)
हल:
माना
P(n) = cos α cos 2α + ............. + cos nα
= sin \(\frac{n \alpha}{2}\) cosec \(\frac{\alpha}{2}\) cos \(\frac{(n+1) \alpha}{2}\)
जब n = 1, तब L.H.S. = cos α
और R.H.S. = sin \(\frac{\alpha}{2}\) cosec \(\frac{\alpha}{2}\) cos α = cos α
∴ L.H.S. = R.H.S.
अत: P (1) सत्य है ।
माना P(k) सत्य है ।
⇒ cos α cos 2α + ............. + cos kα

अत: P(k + 1) सत्य है जब P (k) सत्य है ।
अतः गणितीय आगमन विधि द्वारा सभी प्राकृत संख्या 1 के लिए P(n) सत्य है।

बहुचयनात्मक प्रश्न-

प्रश्न 1.
n ∈ N के लिए 2³ⁿ - 7n - 1 विभाज्य होगा-
(A) 14
(C) 7
(B) 121
(D) 98
हल:
(C) 7

प्रश्न 2.
यदि n सम प्राकृत संख्या है तो n (n² - 1 ) विभाज्य है-
(A) 4
(C) 6
(B) 5
(D) 8
हल:
(C) 6

प्रश्न 3.
n के सभी धनात्मक पूर्णांकों के लिए 2 + 5 + 8 + 11 + .......... + (3n - 1) का मान है-
(A) n(n – 1)
(B) n(n + 1)
(C) n (3n+1)
(D) \(\frac{n(n+3)}{2}\)
हल:
(C) n (3n+1)

प्रश्न 4.
n ∈ N के लिए 2ⁿ > n² जबकि—
(A) n > 2
(C) n < 5 (B) n > 3
(D) n ≥ 5
हल:
(D) n ≥ 5

प्रश्न 5.
n ∈ N के लिए 3ⁿ - 2ⁿ एक-
(A) विषम संख्या है।
(B) सम संख्या है।
(C) दोनों प्रकार की हो सकती है।
(D) एक अभाज्य संख्या है।
हल:
(A) विषम संख्या है।

प्रश्न 6.
यदि n ∈ N तो कौनसा कथन सत्य है-
(A) n⁴ + < 10ⁿ
(B) n² > 2n
(C) 2ⁿ < 2
(D) 2³ⁿ > 7n + 1
हल:
(A) n⁴ + < 10ⁿ

प्रश्न 7.
प्रत्येक धन पूर्णांक 1 के लिए संख्या 7ⁿ - 3ⁿ, किससे विभाजित है-
(A) 4
(C) 6
(B) 5
(D) 7
हल:
(A) 4

प्रश्न 8.
यदि P (n) एक कथन है--" n (n + 1) (n + 2), 12 से भाज्य है।" तो सत्य कथन है-
(A) P(3)
(B) P(4)
(C) P(5)
(D) P(3) व P(4)
हल:
(D) P(3) व P(4)

प्रश्न 9.
यदि P (n) एक कथन है- "10n + 3 एक अभाज्य संख्या है ।" तो सत्य कथन है-.
(A) P(3)
(B) P(2)
(C) दोनों A व B
(D) उपर्युक्त में से कोई नहीं
हल:
(B) P(2)

प्रश्न 10.
3ⁿ > n³, n ∈ N जबकि-
(A) n < 4 (C) n > 2
(B) n ≥ 3.
(D) n ≥ 4
हल:
(D) n ≥ 4

प्रश्न 11.
n ∈ N के लिए 3²ⁿ - 2n + 1 विभाज्य है-
(A) 2 से
(B) 4 से
(C) 12 से
(D) 8 से
हल:
(A) 2 से

प्रश्न 12.
n ∈ N के लिए 7²ⁿ + 16 - 1 विभाज्य है-
(A) 64 से
(B) 128 से
(C) 256 से
(D) इनमें से कोई नहीं
हल:
(A) 64 से

प्रश्न 13.
n ∈ N के लिए n(n - 1) (2n - 1) विभाज्य है—
(A) 12 से
(C) 5 से
(B) 24 से
(D) 6 से
हल:
(D) 6 से

प्रश्न 14.
n ∈ N के लिए 3²ⁿ + 7 विभाज्य है-
(A) 16 से
(B) 9 से
(C) 8 से
(D) 6 से
हल:
(C) 8 से

प्रश्न 15.
P(n) एक कथन हैं-" n² + n, 3 से भाज्य है" तो सत्य कथन
(A) P(4)
(B) P(3)
(C) दोनों
(D) उपर्युक्त में से कोई नहीं
हल:
(B) P(3)

प्रश्न 16.
प्रत्येक प्राकृत संख्या n के लिए n (n² - 1 ) द्वारा विभाजित है-
(A) 4
(B) 6
(C) 10
(D) उपर्युक्त में से कोई नहीं
हल:
(B) 6

प्रश्न 17.
गणितीय आगमन के सिद्धान्त के अनुसार 1³ + 2³ + 3³ + ......................... + n³ बराबर है-
(A) \(\left[\frac{n(n+1)}{2}\right]^2\)
(B) \(\left[\frac{n(n+2)}{2}\right]^2\)
(C) \(\left[\frac{n(n+1)(2 n+1)}{4}\right]^2\)
(D) \(\left[\frac{n(n+2)(n+3)}{2}\right]^2\)
हल:
(A) \(\left[\frac{n(n+1)}{2}\right]^2\)

प्रश्न 18.
धनात्मक पूर्णांक n के लिए, माना a (n) = 1 + \(\frac{1}{2}\) + \(\frac{1}{3}\) + \(\frac{1}{4}\) + ............... + \(\frac{1}{2^n-1}\), तब
(A) a (100) ≤ 100
(B) a (100) > 100
(C) a (200) ≤ 100
(D) a (200) > 100
हल:
(A) a (100) ≤ 100

प्रश्न 19.
n ∈ N के लिए, (2³ⁿ - 1) विभाजित होगा-
(A) 25
(B) 8
(C) 7
(D) 3
हल:
(C) 7

प्रश्न 20.
10ⁿ + 3 (4^{n + 2}) + 5, (n ∈ N) से भाज्य है-
(A) 7
(B) 5
(C) 9
(D) 17
हल:
(C) 9

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
निगमन एक प्रक्रिया है जिसमें एक कथन सिद्ध करने को दिया जाता है जिसे .............................. कहते हैं।
हल:
प्रमेय

प्रश्न 2.
आगमन शब्द का अर्थ विशिष्ट स्थितियों या तथ्यों से .......................... करने से है।
हल:
व्यापकीकरण

प्रश्न 3.
R के किसी भी ऐसे उपसमुच्चय में जो आगमनिक है, .............................. अनिवार्य रूप से समाहित होता है।
हल:
N

प्रश्न 4.
गणितीय आगमन के प्रयोग वाली उपपत्ति के प्रथम चरण में P (1) को सत्य सिद्ध करते हैं, इस चरण को ............................. कहते हैं।
हल:
मूल चरण

प्रश्न 5.
गणितीय आगमन के प्रयोग वाली उपपति में यदि n = k के लिए कथन सत्य है तो यह n = k + 1 के लिए भी सत्य है। इसे ............................ कहा जाता है।
हल:
आगमन का चरण

प्रश्न 6.
प्रथम n प्राकृत संख्याओं का योग = ..........................
हल:
\(\frac{n(n+1)}{2}\)

प्रश्न 7.
प्रथम n प्राकृत संख्याओं के वर्गों का योग = ..........................
हल:
\(\frac{n(n+1)(2 n+1)}{6}\)

प्रश्न 8.
प्रथम n प्राकृत संख्याओं के घनों का योग = ............................
हल:
\(\left(\frac{n(n+1)}{2}\right)^2\)

प्रश्न 9.
यदि xⁿ - 1, x - λ से विभाज्य है, तब λ का न्यूनतम धनात्मक मान = ...........................
हल:
1

प्रश्न 10.
n ∈ N के सभी मानों के लिए 3 × 5^{2n + 1} + 2^{3n + 1}, ................................. से विभाज्य है।
हल:
17

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
1 + 3 + 3² + ..................... + 3^{n - 1} = \(\frac{3^n-2}{2}\), ∀ n ∈ N
हल:
असत्य

प्रश्न 2.
प्रथम n विषम प्राकृत संख्याओं का योग n² होता है|
हल:
सत्य

प्रश्न 3.
\(\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+\ldots \ldots . .+\frac{1}{(3 n-1)(3 n+2)}=\frac{n}{6 n+4}\), ∀ n ∈ N
हल:
सत्य

प्रश्न 4.
\(\frac{1}{1.4}+\frac{1}{4.7}+\frac{1}{7.10}+\ldots \ldots+\frac{1}{(3 n-2)(3 n+1)}=\frac{n}{3 n+2}\), ∀ n ∈ N
हल:
असत्य

प्रश्न 5.
\(\frac{1}{3.5}+\frac{1}{5.7}+\frac{1}{7.3}+\ldots \ldots . .+\frac{1}{(2 n+1)(2 n+3)}=\frac{n}{3(2 n+3)}\), ∀ n ∈ N
हल:
सत्य

प्रश्न 6.
1.2 + 2.2² + 3.2² + ................ + n.2 = (n - 1)2^{n + 1} + 2, ∀ n ∈ N
हल:
सत्य

प्रश्न 7.
2 + 5 + 8 + 11 + ................... + (3n - 1) = \(\frac{1}{2}\)n (3n - 1), ∀ n ∈ N
हल:
असत्य

प्रश्न 8.
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots \ldots . .+\frac{1}{2^n}=1+\frac{1}{2^n}\), ∀ n ∈ N
हल:
असत्य

प्रश्न 9.
5^{2n - 1}, n ∈ N के प्रत्येक मान के लिए 24 से विभाज्य है।
हल:
सत्य

प्रश्न 10.
\(\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)\left(1+\frac{1}{3}\right) \ldots \ldots \ldots\left(1+\frac{1}{m}\right)\) = m + 2, ∀ n ∈ N
हल:
असत्य

सही मिलान कीजिए-

हल:
1. (d)
2. (f)
3. (a)
4. (b)
5. (e)
6. (j)
7. (h)
8. (i)
9. (c)
10. (g)