RBSE Class 11 Maths Important Questions Chapter 3 त्रिकोणमितीय फलन

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 3 त्रिकोणमितीय फलन Important Questions and Answers.

RBSE Class 11 Maths Chapter 3 Important Questions त्रिकोणमितीय फलन

अतिलघूतरात्मक प्रश्न- 

प्रश्न 1.
sin ( - 330°) का मान लिखिए ।
हल:
sin (- 330°) = - sin 330° ∵ sin (- θ) = - sin θ
= sin (360° - 30°)
= - [ - sin 30° ]
[∵ sin (2π - θ) = - sin θ] = sin 30°

प्रश्न 2.
cos x = \(\frac{1}{2}\) को हल कीजिए ।
हल:
हम पाते हैं cos x = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
इसलिए x = 2nπ ± \(\frac{\pi}{3}\) जहाँ n ∈ I

प्रश्न 3.
यदि cos 3θ = \(\frac{\sqrt{3}}{2}\) हो, तो θ का व्यापक मान लिखिए।
हल:
cos 3θ = \(\frac{\sqrt{3}}{2}\) = cos \(\frac{\pi}{6}\)
∴ 3θ = 2nπ ± \(\frac{\pi}{6}\)
⇒ θ = \(\frac{2 n \pi}{3} \pm \frac{\pi}{18}\)

प्रश्न 4.
यदि sin A = - 1 हो, तो A का मान ज्ञात कीजिए।
हल:
sin A = - 1

प्रश्न 5.
cos 7θ cos 3θ को योग एवं अन्तर के रूप में लिखिए।
हल:
cos 7θ cos 3θ = \(\frac{1}{2}\) [2 cos 7θ cos 3θ]
= \(\frac{1}{2}\) [cos (7θ + 3θ) + cos (7θ - 3θ)]
= \(\frac{1}{2}\) [cos 10θ + cos 40]

प्रश्न 6.
sin \(\frac{5 \pi}{12}\) sin \(\frac{\pi}{12}\) का मान लिखिए ।
हल:

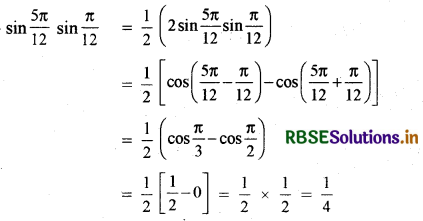
प्रश्न 7.
यदि tan α = \(\frac{3}{4}\), तो tan 3α का मान लिखिए।
हल:

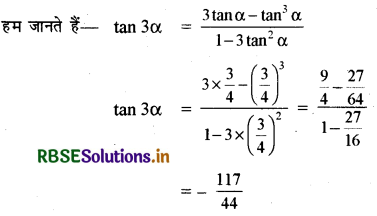
प्रश्न 8.
sin²24° - sin² 6° का मान लिखिए ।
हल:
⇒ sin²24° - sin² 6°
⇒ sin (24° + 6°) sin (24° - 6°)
⇒ sin 30° sin 18° = \(\frac{1}{2} \times\left(\frac{\sqrt{5}-1}{4}\right)\)
⇒ \(\frac{1}{8}\) (√5 - 1)

प्रश्न 9.
व्यंजक \(\frac{2 \tan A}{\tan 2 A}\) का मान tan A के पदों में ज्ञात कीजिए।
हल:

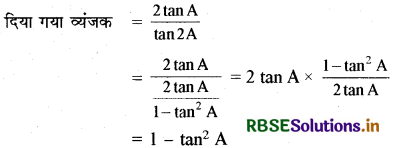
प्रश्न 10.
व्यंजक {cos A . cos (90° - A ) } का मान ज्ञात कीजिए।
हल:
दिया गया व्यंजक
= cos A cos (90° – A)
= cos A . sin A
= sin A . cos A = \(\frac{1}{2}\) × 2 sin A . cos A
= \(\frac{1}{2}\) sin 2A

प्रश्न 11.
यदि cos 2θ = cos²θ हो तो θ का व्यापक मान ज्ञात कीजिए ।
हल:
प्रश्नानुसार cos 2θ = cos²θ
या 2 cos 2θ = 2 cos²θ
या 2 cos 2θ = cos 2θ + 1
या cos 2θ = 1
या cos 2θ = cos 0
∴ 2θ = 2nπ ± 0
या θ = nπ

प्रश्न 12.
यदि tan 5θ = cot 2θ हो, तो 6 का व्यापक मान ज्ञात कीजिए ।
हल:
दिया है, tan 5θ = cot 2θ

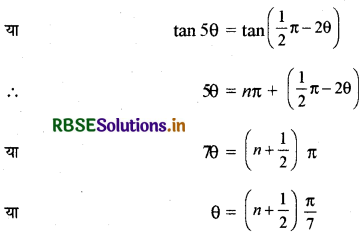
प्रश्न 13.
tan 105° का मान ज्ञांत कीजिए।
हल:

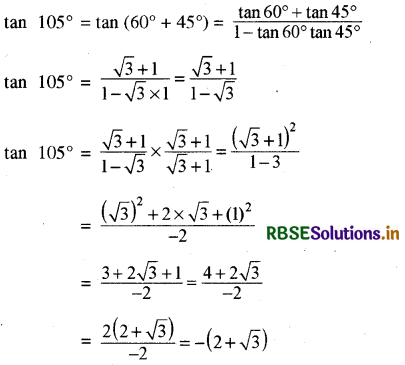
लघूत्तरात्मक प्रश्न

प्रश्न 1.
यदि sin θ = \(\frac{12}{13}\) और θ द्वितीय चतुर्थांश में हो तो sec θ + tan θ का मान ज्ञात कीजिए।
हल:
हम जानते हैं कि
sin²θ + cos²θ = 1
⇒ cos θ = ± \(\sqrt{1-\sin ^2 \theta}\)
cos θ, द्वितीय चतुर्थांश में ऋणात्मक है।

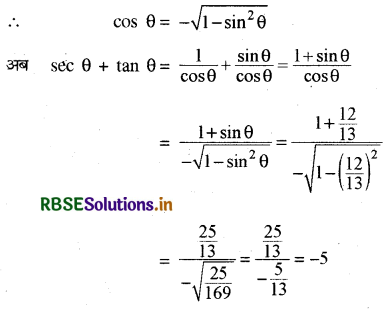
प्रश्न 2.
चतुर्भुज ABCD में सिद्ध कीजिए-
(i) sin (A + B) + sin (C + D) = 0
(ii) cos (A + B) = cos (C + D)
हल:
(i) हम जानते हैं कि किसी भी चतुर्भुज में
A + B + C + D = 2π
⇒ A + B = 2π - (C + D)
⇒ sin (A + B) = sin [2π - (C + D)]
⇒ sin (A + B) = - sin (C + D) [∵ sin (2π - θ) = - sin θ]
⇒ sin(A + B) + sin (C + D) = 0

(ii) हम जानते हैं
A + B + C + D = π
⇒ (A + B) = 2π - (C + D)
⇒ cos (A + B) = cos [2π - (C + D)]
⇒ cos (A + B) = cos (C + D) [∵ cos (2π - θ) = cos θ]

प्रश्न 3.
cos θ का मान ज्ञात कीजिए जिसके लिए समीकरण 2 cos θ = x + \(\frac{1}{x}\) सम्भव है, x वास्तविक है।
हल:
दिया गया समीकरण
2 cos θ = x + \(\frac{1}{x}\)
⇒ 2 cos θ = \(\frac{x^2+1}{x}\)
⇒ x² + 1 - 2x cos θ = 0
⇒ x² - 2 cos θ . x + 1 = 0 .............. (1)
चूँकि x वास्तविक है, समीकरण (1) का विविक्तर अवयव शून्य से बड़ा होना चाहिए।
4 cos²θ - 4 ≥ 0
⇒ 4 (cos²θ - 1) ≥ 0 ⇒ cos²θ ≥ 1
लेकिन cos²θ, 1 से बड़ा नहीं हो सकता
∴ cos²θ = 1 ⇒ cos θ = ± 1

प्रश्न 4.
सिद्ध कीजिए-
sin (n + 1) A sin (n + 2) A + cos (n + 1) A cos (n + 2)A = cos A
हल:
L.H.S. = sin (n + 1) A sin (n + 2) A + cos (n + 1) A cos (n + 2)A
⇒ cos (n + 2) A cos (n + 1)A + sin (n + 2) A sin (n + 1)A
⇒ cos [(n + 2) A - (n + 1)A] = cos [(n + 2 - n - 1)A
= cos A = RHS

प्रश्न 5.
सिद्ध कीजिए-
\(\frac{\sin (A-B)}{\cos A \cos B}+\frac{\sin (B-C)}{\cos B \cos C}+\frac{\sin (C-A)}{\cos C \cos A}\)
हल:
L.H.S. का प्रथम पद हल करने पर

इसी प्रकार द्वितीय पद = tan B - tan C
और तृतीय पद = tan C - tan A
तीनों पदों के मानों को जोड़ने पर
tan A - tan B + tan B - tan C + tan C - tan A
⇒ 0 = R.H.S.

प्रश्न 6.
यदि A + B = 45°, सिद्ध कीजिए
(cot A - 1) (cot B - 1) = 2
हल:
दिया है- A + B = 45°
⇒ cot (A + B) = cot 45° = 1

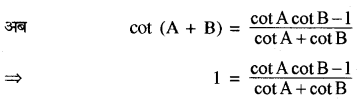
⇒ cot A cot B = cot. A cot B - 1
⇒ cot A cot B - cot A - cot B = 1
दोनों तरफ 1 जोड़ने पर
⇒ 2 = cot A cot B - cot A cot B + 1
⇒ 2 = cot A (cot B - 1) - 1 (cot B - 1)
⇒ 2 = (cot A - 1) (cot B - 1)
या ⇒ (cot A - 1) (cot B - 1) = 2

प्रश्न 7.
सिद्ध कीजिए-
sec\(\left(\frac{\pi}{4}+\theta\right)\) sec\(\left(\frac{\pi}{4}-\theta\right)\) = 2 sec 2θ
हल:

प्रश्न 8.
यदि tan θ = \(\frac{a}{b}\), सिद्ध कीजिए-
b cos 2θ + a sin 2θ = b
हल:
दिया है- tan θ = \(\frac{a}{b}\)
अब L.H.S. b cos 2θ + a sin 2θ
सूत्रों का प्रयोग करने पर

समीकरण हल कीजिए-

प्रश्न 9.
4 sin²θ - 8 cos θ + 1 = 0
हल:
दिया गया है-
4 sin²θ - 8 cos θ + 1 = 0
⇒ 4(1 - cos²θ) - 8 cos θ + 1 = 0
⇒ 4 - 4 cos²θ - 8 cos θ + 1 = 0
⇒ 4 cos²θ + 8 cos θ - 5 = 0
⇒ 4 cos²θ + 10 cos θ - 2 cos θ - 5 = 0
⇒ 2 cos θ (2 cos θ + 5) 1 (2 cos θ + 5) = 0
⇒ (2 cos θ - 1) (2 cos θ + 5) = 0
⇒ 2 cos θ + 5 तथा 2 cos θ - 1 = 0

Case I जब 2 cos θ + 5 = 0
⇒ cos θ = - \(\frac{5}{2}\) जो कि सम्भव नहीं है

Case II जब 2 cos θ - 1 = 0
⇒ cos θ = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
सूत्र से ∴ θ = 2nπ ± α से
θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ I

प्रश्न 10.
किसी त्रिभुज के लिए सिद्ध कीजिए-
tan 2A. tan 2B. tan 2C = tan 2A + tan 2B + tan 2C
हल:
∵ हम जानते हैं कि
A + B + C = 180°
⇒ ∴ 2A + 2B + 2C = 360°
⇒ 2A + 2B = 360° - 2C
(दोनों पक्षों का tangent लेने पर )
⇒ tan (2A + 2B) = tan (360° - 2C)
⇒ \(\frac{\tan 2 \mathrm{~A}+\tan 2 \mathrm{~B}}{1-\tan 2 \mathrm{~A} \cdot \tan 2 \mathrm{~B}}\) = - tan 2C
[∵ tan (180° - θ) = - tan θ]
⇒ tan 2A + tan 2B = - tan 2C . (1 - tan 2A . tan 2B)
⇒ tan 2A + tan 2B = - tan 2C + tan 2A . tan 2B . tan 2C
⇒ tan 2A + tan 2B + tan 2C = tan 2A. tan 2B. tan 2C
या tan 2A . tan 2B . tan 2C = tan 2A + tan 2B + tan 2C

प्रश्न 11.
सिद्ध कीजिए-
\(\frac{1+\sin 2 \theta-\cos 2 \theta}{1+\sin 2 \theta+\cos 2 \theta}\) = tan θ
हल:

प्रश्न 12.
सिद्ध कीजिए कि-
sin²\(\frac{\pi}{18}\) + sin²\(\frac{\pi}{9}\) + sin²\(\frac{7 \pi}{18}\) + sin²\(\frac{4 \pi}{9}\) = 2
हल:
L.H.S. =  sin²\(\frac{\pi}{18}\) + sin²\(\frac{\pi}{9}\) + sin²\(\frac{7 \pi}{18}\) + sin²\(\frac{4 \pi}{9}\)
= sin² 10° + sin² 20° + sin² 70° + sin² 80°
= sin² (90° - 80°) + sin² (90° - 70°) + sin² 70° + sin² 80°
= cos² 80° + cos² 70° + sin² 70° + sin² 80° [∵ sin (90 - θ) = cos θ]
= (cos² 80° + sin² 80°) + (cos² 70° + sin² 70°)
= 1 + 1
= 2 = R.H.S.

निबन्धात्मक प्रश्न-

प्रश्न 1.
सिद्ध कीजिए—
4 sin α . sin (α + \(\frac{\pi}{3}\)) sin (α + \(\frac{2 \pi}{3}\)) = sin 3α
हल:

= sin α + 2 sin α cos 2α
= sin α + [sin(α + 2α) - sin (2α - α)
∵ 2 cos A cos B = sin(A + B) - sin (A - B)]
= sin α + sin 3α - sin α = sin 3α = R.H.S.

प्रश्न 2.
हल कीजिए-
(i) tan 3x + tan 4x + tan 7x = tan 3x tan 4x tan 7x
(ii) tan x + tan 4x + tan 7x = tan x . tan 4x tan 7x
हल:
(i) tan 3x + tan 4x + tan 7x = tan 3x tan 4x tan 7x
⇒ tan 3x + tan 4x = tan 3x + tan 4x tan 7x - tan 7x
⇒ tan 3x + tan 4x = - tan 7x (1 - tan 3x tan 4x)
⇒ \(\frac{\tan 3 x+\tan 4 x}{1-\tan 3 x \tan 4 x}\) = - tan 7x
⇒ tan 7x = - tan 7x
⇒ 2 tan 7x = 0
⇒ tan 7x = 0
⇒ 7x = nπ
⇒ x = \(\frac{n \pi}{7}\), n ∈ I

(ii) tan x + tan 4x + tan 7x = tan x tan 4x tan 7x
⇒ tan x tan 4x = tan x + tan 4x tan 7x- tan 7x
⇒ tan x + tan 4x = - tan 7x (1 - tan x . tan 4x)
⇒ \(\frac{\tan x+\tan 4 x}{1-\tan x \cdot \tan 4 x}\) = - tan 7x
⇒ tan (x + 4x) = - tan 7x
⇒ tan 5x = - tan 7x = tan (- 7x) ∵ tan (- θ) = - tan θ
⇒ 5x = nπ + (- 7x)
⇒ 12x = nπ
⇒ x = \(\frac{n \pi}{12}\), n ∈ I

प्रश्न 3.
यदि tan (A + B) = n tan (A - B) हो, तो प्रदर्शित कीजिए-
(n + 1) sin 2B (n - 1) sin 2A
हल:
दिया हुआ है कि

प्रश्न 4.
4 cos θ - 3 sec θ = tan θ
हल:
दी हुई समीकरण है-
4 cos θ - 3 sec θ = tan θ
⇒ 4 cos θ - \(\frac{3}{\cos \theta}\) = \(\frac{\sin \theta}{\cos \theta}\)
⇒ 4 cos²θ - 3 = sin θ
⇒ 4(1 - sin²θ) - 3 = sin θ
⇒ 4 - 4 sin²θ - 3 = sin θ
⇒ 1 - 4 sin²θ = sin θ
⇒ 4 sin²θ + sin θ - 1 = 0

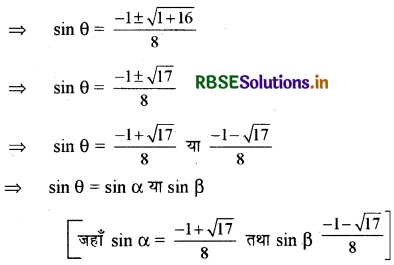
यदि sin θ = sin α
⇒ θ = nπ + (- 1)ⁿ α
तथा यदि sin θ = sin β
⇒ θ = nл + (- 1)ⁿ β
अतः दी हुई समीकरण के अभीष्ट हल हैं-
⇒ θ = nπ + (- 1)ⁿ α
तथा θ = nπ + (- 1)ⁿ β, n ∈ I
जहाँ α = sin^-1 \(\left(\frac{-1+\sqrt{17}}{8}\right)\)
तथा β = sin^-1 \(\left(\frac{-1-\sqrt{17}}{8}\right)\)

प्रश्न 5.
निम्न त्रिकोणमितीय समीकरण का हल कीजिए-
sin θ + sin 2θ + sin 3θ = 0
हल:
दिया गया समीकरण
sin θ + sin 2θ+ sin 3θ = 0
या sin θ + sin 3θ + sin 2θ = 0
या 2 sin \(\frac{(\theta+3 \theta)}{2}\) cos \(\frac{(\theta-3 \theta)}{2}\) + sin 2θ = 0
या 2 sin 2θ cos θ + sin 2θ = 0
या sin 2θ (2 cos θ + 1) = 0

प्रश्न 6.
सिद्ध कीजिए कि -
tan (45° + \(\frac{1}{2}\)) = \(\sqrt{\frac{1+\sin \phi}{1-\sin \phi}}\)
हल:

बहुचयनात्मक प्रश्न-

प्रश्न 1.
यदि sin A = \(\frac{3}{5}\) तथा cos B = \(\frac{9}{41}\) हो एवं A तथा B न्यून कोण हों, तो cos (A + B) का मान होगा-
(A) - \(\frac{133}{205}\)
(B) - \(\frac{84}{205}\)
(C) \(\frac{84}{205}\)
(D) \(\frac{133}{205}\)
हल:
(B) -\(\frac{84}{205}\)

प्रश्न 2.
यदि sin α + sin β = a तथा cos α + cos β = b हो, तो cos (α - β) का मान होगा-
(A) \(\frac{1}{2}\) (a² + b² - 2)
(B) \(\frac{1}{2}\) (a² + b² + 2)
(C) \(\frac{1}{2}\) (a² - b² - 2) .
(D) \(\frac{1}{2}\) (- a² + b² + 2)
हल:
(A) \(\frac{1}{2}\) (a² + b² - 2)

प्रश्न 3.
यदि \(\frac{\sin (x+y)}{\sin (x-y)}=\frac{a+b}{a-b}\) हो, तो \(\frac{\tan x}{\tan y}\) का मान होगा—
(A) \(\frac{a}{b}\)
(B) \(\frac{b}{a}\)
(C) \(\frac{a^2}{b^2}\)
(D) a. b
हल:
(A) \(\frac{a}{b}\)

प्रश्न 4.
समीकरण sec²θ = 2 हो तो θ का व्यापक मान होगा-
(A) 2nπ ± \(\frac{\pi}{4}\)
(B) nπ ± (-1)ⁿ \(\frac{\pi}{4}\)
(C) nπ ± \(\frac{\pi}{2}\)
(D) nπ ± \(\frac{\pi}{4}\)
हल:
(A) 2nπ ± \(\frac{\pi}{4}\)

प्रश्न 5.
समीकरण tan 3θ = tan θ हो, तो θ का व्यापक मान होगा-
(A) \(\frac{n \pi}{3}\)
(B) \(\frac{n \pi}{4}\)
(C) \(\frac{2n \pi}{3}\)
(D) \(\frac{n \pi}{2}\)
हल:
(D) \(\frac{n \pi}{2}\)

प्रश्न 6.
यदि sin θ = 0 हो, तो θ का व्यापक मान होगा-
(A) nπ
(B) 0
(C) 2πr
(D) nπ + (- 1)n \(\frac{\pi}{2}\)
हल:
(A) nπ

प्रश्न 7.
यदि A + B + C = ग हो, तो tan \(\left(\frac{A+B}{2}\right)\) का मान है-
(A) tan C
(B) tan \(\frac{C}{2}\)
(C) cot \(\frac{C}{2}\)
(D) - cot C
हल:
(C) cot \(\frac{C}{2}\)

प्रश्न 8.
tan 3A tan 2A - tan A
(A) tan 3A tan 2A tan A
(B) - tan 3A tan 2A tan A
(C) tan A tan 2A - tan 2A tan 3A - tan 3A tan A
(D) 0
हल:
(A) tan 3A tan 2A tan A

प्रश्न 9.
cos 960° का मान है-
(A) \(\frac{1}{2}\)
(B) \(\frac{\sqrt{3}}{2}\)
(C) - \(\frac{\sqrt{3}}{2}\)
(D) - \(\frac{1}{2}\)
हल:
(A) \(\frac{1}{2}\)

प्रश्न 10.
यदि A + B + C = 90° हो तो tan (B + C) का मान होगा-
(A) tan A
(B) - tan A
(C) cot A
(D) - cot A
हल:
(C) cot A

प्रश्न 11.
cos (- 660°) का मान है-
(A) \(\frac{\sqrt{3}}{2}\)
(B) - \(\frac{1}{2}\)
(C) \(\frac{1}{2}\)
(D) \(\frac{1}{\sqrt{2}}\)
हल:
(C) \(\frac{1}{2}\)

प्रश्न 12.
550° का कोण अनुरेखित करने में परिक्रामी रेखा की स्थिति होगी-
(A) प्रथम चतुर्थांश में
(B) द्वितीय चतुर्थांश में
(C) तृतीय चतुर्थांश में
(D) चतुर्थ चतुर्थांश में
हल:
(C) तृतीय चतुर्थांश में

प्रश्न 13.
2 cos A cos B बराबर है-
(A) cos (A + B) cos (A - B)
(B) cos (A + B) + cos (A - B)
(C) cos (AB) - cos (A + B)
(D) इनमें से कोई नहीं
हल:
(B) cos (A + B) + cos (A - B)

प्रश्न 14.
2 sin A sin B बराबर है-
(A) sin (A + B) + sin (A - B)
(B) sin (A + B) - sin (A - B)
(C) cos (A + B) + cos (A - B)
(D) cos (A - B) - cos (A + B)
हल:
(D) cos (A - B) - cos (A + B)

प्रश्न 15.
If A + B + C = \(\frac{\pi}{2}\) हो, तो sin (A + B) का मान है-
(A) sin C
(B) cos C
(C) - sin C
(D) cos C
हल:
(B) cos C

प्रश्न 16.
यदि sin²θ = 3 cos²θ हो, तो θ के मान होंगे-
(A) 60°, 120°, 240°, 300°
(B) 60°, 120°, 240°, 315°
(C) 60°, 150°, 240°, 300°
(D) 60°, 120°, 210°, 315°
हल:
(A) 60°, 120°, 240°, 300°

प्रश्न 17.
यदि tan α = \(\frac{5}{6}\) तथा tan β = \(\frac{1}{11}\) तो tan (α + β) का मान होगा-
(Α) π
(B) \(\frac{\pi}{2}\)
(C) \(\frac{\pi}{4}\)
(D) 0
हल:
(C) \(\frac{\pi}{4}\)

प्रश्न 18.
यदि tan (A + B) = p तथा tan (A - B) = 9 हो, तो tan 2A का मान p तथा 9 पदों में है-
(A) \(\frac{p+q}{p-q}\)
(B) \(\frac{p-q}{1+p q}\)
(C) \(\frac{p+q}{1-p q}\)
(D) \(\frac{1+p q}{1-p}\)
हल:
(C) \(\frac{p+q}{1-p q}\)

प्रश्न 19.
sin (60° - A) cos (30° – B) + cos (60° – A) sin (30° - B) का मान होगा-
(A) sin (A + B)
(B) sin (A - B)
(C) cos (A + B)
(D) cos (A - B)
हल:
(C) cos (A + B)

प्रश्न 20.
cos² - sin²\(\left(\frac{\pi}{8}-\frac{x}{2}\right)\) का मान है-
(A) √2 cos x
(B) \(\frac{1}{\sqrt{2}}\) cos x
(C) 2 sin \(\frac{x}{2}\)
(D) 2 cos \(\frac{x}{2}\)
हल:
(B) \(\frac{1}{\sqrt{2}}\) cos x

प्रश्न 21.
cos (45° - A) cos (45° - B) - sin (45° - A) sin (45° - B) बराबर है-
(A) sin (A + B)
(B) sin (A - B)
(C) cos (A + B)
(D) cos (A - B)
हल:
(A) sin (A + B)

प्रश्न 22.
sin 3A बराबर है-
(A) 3 sin A - 4 sin³A
(B) sin A + 4 sin³A
(C) 4 sin³A - 3 cos A
(D) इनमें से कोई नहीं
हल:
(A) 3 sin A - 4 sin³A

प्रश्न 23.
cos 3A बराबर हैं-
(A) 3 cos A 4 cos³A
(B) 3 cos A + 4 cos³A
(C) 4 cos³A - 3 cos A
(D) इनमें से कोई नहीं
हल:
(C) 4 cos³A - 3 cos A

प्रश्न 24.
cos 15° - sin 15° का मान है
(A) - \(\frac{1}{\sqrt{2}}\)
(B) √2
(C) -√2
(D) \(\frac{1}{\sqrt{2}}\)
हल:
(D) \(\frac{1}{\sqrt{2}}\)

प्रश्न 25.
यदि α + β + r = 2π, तो-

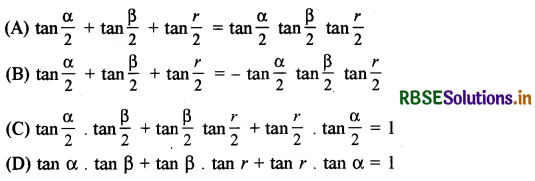
हल:
(A) tan \(\frac{\alpha}{2}\) + tan \(\frac{\beta}{2}\) + tan \(\frac{r}{2}\) = tan \(\frac{\alpha}{2}\) tan \(\frac{\beta}{2}\) tan \(\frac{r}{2}\)

प्रश्न 26.
यदि A + B+ С = л हो, तो tan A + tan B + tan C का मान बराबर है-
(A) tan A tan B + tan B tan C + tan C tan A
(B) (tan A tan B + tan B tan C + tan C tan A)
(C) tan A tan B tan C
(D) - tan A tan B tan C
हल:
(C) tan A tan B tan C

प्रश्न 27.
यदि \(\frac{1+\cos 2 \theta}{1-\cos 2 \theta}\) = 3 हो, तो θ का व्यापक मान होगा-
(A) nл ± \(\frac{\pi}{6}\)
(B) 2nл ± \(\frac{\pi}{6}\)
(C) nл ± \(\frac{\pi}{3}\)
(D) 2nл ± \(\frac{\pi}{3}\)
हल:
(A) nл ± \(\frac{\pi}{6}\)

प्रश्न 28.
यदि 25 cos²θ + 5 cos θ - 12= 0, \(\frac{\pi}{2}\) < α < л का एक मूल α हो, तब sin 2α बराबर होगा-
(A) 24/25
(B) - 24/25
(C) 13/18
(D) - 13/18
हल:
(B) - 24/25

प्रश्न 29.
यदि θ और Φ न्यून कोण हैं sin θ = \(\frac{1}{2}\), cos Φ = \(\frac{1}{3}\) को सन्तुष्ट करते हैं, तब θ + Φ ∈ :

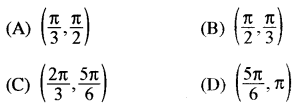
हल:
(B) \(\left(\frac{\pi}{2}, \frac{\pi}{3}\right)\)

प्रश्न 30.
यदि sin (α + β) = 1, sin (α - β) = \(\frac{1}{2}\) तब tan (α + 2β) tan (2α + β) बराबर है-
(A) 1
(B) - 1
(C) 0
(D) उपर्युक्त में कोई नहीं
हल:
(A) 1

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
रेडियन माप = ...................................
हल:
\(\frac{\pi}{180}\) × डिग्री माप

प्रश्न 2.
1° = ...................................
हल:
\(\frac{\pi}{180}\) रेडियन

प्रश्न 3.
1 रेडियन = \(\frac{180^{\circ}}{\pi}\) = ...................................
हल:
57°16' निकटतम

प्रश्न 4.
sin x = 0 है तब x = .................................., जहाँ n कोई पूर्णांक है।
हल:
nπ

प्रश्न 5.
cos x = 0 है तब x = ..................................., जहाँ n कोई पूर्णांक है ।
हल:
(2n + 1)\(\frac{\pi}{2}\)

प्रश्न 6.
sin \(\frac{31 \pi}{3}\) का मान ................................... है।
हल:
\(\frac{\sqrt{3}}{2}\)

प्रश्न 7.
tan \(\frac{31 \pi}{12}\) का मान ................................... है।
हल:
2 - √3

प्रश्न 8.
समीकरण tan x = - \(\frac{1}{\sqrt{3}}\) का मुख्य मान ................................... है।
हल:
\(\frac{5 \pi}{6}\) तथा \(\frac{11 \pi}{6}\)

प्रश्न 9.
cos \(\left(-\frac{8 \pi}{3}\right)\) = ...............................
हल:
- \(\frac{1}{2}\)

प्रश्न 10.
यदि cot x tan x = secx, तब x = .................................
हल:
nπ + (- 1)ⁿ\(\frac{\pi}{6}\), n ∈ Z

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
इकाई त्रिज्या के वृत्त की परिधि 21 होती है ।
हल:
सत्य

प्रश्न 2.
40°20′ का रेडियन माप \(\frac{121}{540}\) रेडियन होता है।
हल:
असत्य

प्रश्न 3.
sin \(\left(\frac{31 \pi}{3}\right)\), का मान - \(\frac{\sqrt{3}}{2}\) होता है।
हल:
असत्य

प्रश्न 4.
sin \(\left(\frac{151 \pi}{6}\right)\) का मान - \(\frac{\sqrt{1}}{2}\) होता है।
हल:
सत्य

प्रश्न 5.
cos(cos x) का अधिकतम मान 1 तथा न्यूनतम मान cos 1 है।
हल:
सत्य

प्रश्न 6.
sin(cos x) का अधिकतम मान 1 है।
हल:
असत्य

प्रश्न 7.
sin 1° < sin 1
हल:
सत्य

प्रश्न 8
tan 1° tan 2° tan 3° ......................... tan 89° का मान 1 है।
हल:
सत्य

प्रश्न 9.
cos 1°. cos 2° cos 3° ........................... cos 179° का मान 1 है|
हल:
असत्य

प्रश्न 10.
यदि tan α = \(\frac{x}{x+1}\) और tan β = \(\frac{1}{x+1}\), तब α + β का मान \(\frac{\pi}{6}\) होगा ।
हल:
असत्य

सही मिलान कीजिए

हल:
1. (c)
2. (j)
3. (e)
4. (a)
5. (h)
6. (f)
7. (b)
8. (i)
9. (d)
10. (g)