RBSE Class 11 Maths Important Questions Chapter 3 Trigonometric Functions

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 3 Trigonometric Functions
Important Questions and Answers.

RBSE Class 11 Maths Chapter 3 Important Questions Trigonometric Functions

Question 1.
Show that:
cos² (45° + x) - sin² (45° - x), is independent of x.
Answer:
L.H.S. cos² (45° + x) - sin² (45° - x)
= cos (45° + x + 45° - x) . cos [45° + x - (45° - x)]
= cos (90°) cos(45° + x - 45° + x)
[∵ cos² A - sin² B = cos(A + B) cos(A - B)]
= cos 90°. cos 2x
= (0) cos 2x 0
which is independent of x.
R.H.S.
Hence Proved.

Question 2.
If sin x = $\frac{4}{5}$, cos y = - $\frac{5}{13}$ where x and y both lies in second quadrant, find the value of sin(x + y).
Answer:
sin(x + y) = sin x cos y + cos x sin y
‘Now cos² x = 1 - sin² x {∵ sin² θ + cos² θ = 1)
= 1 - $\frac{16}{25}$ = $\frac{25-16}{25}$ = $\frac{9}{25}$
Thus, cos x = ± $\frac{3}{5}$,
Since x lies in second quadrant so cos x will be negative.
Then, cos x = $\frac{3}{5}$
Again, sin² y = 1 - cos² y = 1 - $\left(-\frac{5}{13}\right)^2$
{Using formula sin² θ + cos² θ = 1}
= 1 - $\frac{25}{169}$
sin²y = $\frac{144}{169}$
Thus, sin y = ± $\frac{12}{13}$
Whereas y lies in second quadrant so, sin y will be positive. Thus,
Putting value of sin x, cos y, cos x and sin y in equation (1)
From equation (1)
sin (x + y) = sin x cos y + cos x sin y

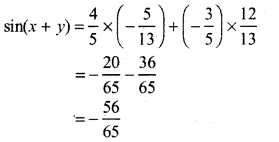
Question 3.
Prove that:
sin $\frac{x}{2}$ sin $\frac{7x}{2}$ + sin $\frac{3x}{2}$ sin $\frac{11x}{2}$ = sin 2x - sin 5x
Answer:

Question 4.
Prove that:
sin² $\left(\frac{\pi}{8}+\frac{x}{2}\right)$ - sin² $\left(\frac{\pi}{8}-\frac{x}{2}\right)$ = sin $\frac{\pi}{4}$ sin x = $\frac{1}{\sqrt{2}}$ sin x
Answer:

Question 5.
If A is in third quadrant and 3 tan A - 4 = 0 then prove that 5 sin 2A + 3 sin A + 4 cos A = 0
Answer:
We have 3 tan A - 4 = 0
⇒ tan A = $\frac{4}{3}$
Since, A lies in third quadrant
∴ sin A and cos A will be negative
⇒ cos A = - $\frac{3}{5}$
⇒ sin A = - $\frac{4}{5}$
∴ L.H.S. = 5 sin 2A + 3 sin A + 4 cos A
= 10 sin A cos A + 3 sin A + 4 cos A [∵ sin 2θ = 2 sin θ cos θ]

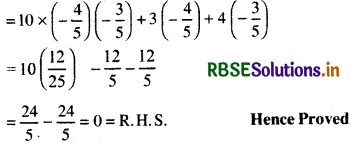
Question 6.
If sin x₁ + sin x₂ + sin x₃ = 3 then prove that cos x₁ + cos x₂ + cos x₁ = 0
Answer:
We have
sin x₁ + sin x₂ + sin x₃ = 3
It is possible only when sin x₁ = sin x₁ = sin x₃ = 1 [- 1 ≤ sin x ≤ 1]
⇒ x₁ = x₂ = 3
∴ L.H.S. = cos x₁ + cos x₂ + cos x₃
= cos $\frac{\pi}{2}$ + cos $\frac{\pi}{2}$ + cos $\frac{\pi}{2}$
= 0 + 0 + 0 = 0
= 0 = R.H.S.
Hence Proved

Question 7.
If cos α + cos β = 0 = sin α + sin β then prove that cos 2α + cos 2β = - 2 cos(α + β)
Answer:
We have
L.H.S. = (cos α + cos β) = (sin α + sin β) = 0
(cos α + cos β)² = (sin α + sin β)²
[By squaring both sides]
= cos²α + cos²β + 2 cos α cos β = sin² α + sin²β + 2 sin α sin β
= cos² α - sin² α + cos²β - sin²β + 2(cos α cos β - sin α sin β) = 0
= cos 2α + cos 2β + 2 cos (α + β) = 0
[∵ cos 2θ cos² θ - sin² θ]
= cos 2α + cos 2β = - 2 cos (α + β)
= R.H.S.
Hence Proved

Question 8.
Prove that
cos x cos y = cos²$\frac{x-y}{2}$ - sin² $\frac{x+y}{2}$
Answer:

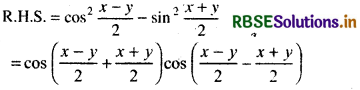
[∵ cos²A - sin² B = cos (A + B) cos (A - B)
= cos x cos (- y)
= cos x cos y [∵ cos (- θ) = cos θ]
= R.H.S.
Hence Proved

Question 9.
If $\frac{\sin (x+y)}{\sin (x-y)}=\frac{a+b}{a-b}$ then prove that $\frac{\tan x}{\tan y}=\frac{a}{b}$.
Answer:

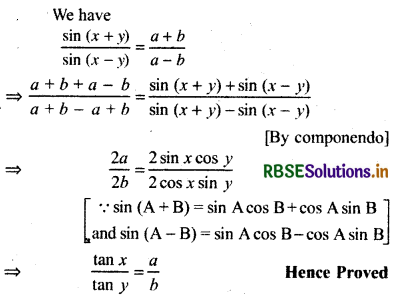
Question 10.
Prove that
tan A + 2 tan 2A + 4 tan 4A + 8 cot 8A = cot A
Answer:

Similarly, tan 2A = cot 2A - 2 cot 4A
and tan 4A = cot 4A - 2 cot 8A
Then, L.H.S. = tan A + 2 tan 2A + 4 tan 4A + 8cot 8A
= (cot A - 2 cot 2A) + 2(cot 2A - 2 cot 4A) + 4(cot 4A - 2 cot 8A) + 8 cot 8A
= cot A - 2 cot 2A + 2 cot 2A - 4cot 4A + 4cot 4A - 8 cot 8A + 8 cot 8A
= cot A = R.H.S.
Hence Proved

Question 11.
If angle A, B and C of ∆ ABC are such that sin (2A + B) = sin (C - A) = - sin (B + 2C) = $\frac{1}{2}$ and A, B and C are in A.P then find value of A, B and C.
Answer:
In ∆ ABC
A + B + C = 180°
and 2B = A + C [AB and C are in A.P]
∴ 2B + B = 180°
⇒ 3B = 180°
⇒ B = 60°
∴ A + C = 120°
We have sin (2A + B) = $\frac{1}{2}$
[Other values of 2A + B cannot be given because then value of A will be greater than 180°]
∴ 2A + B = 150°
2A + 60° = 150°
⇒ 2A =150° - 60°
⇒ 2A = 90°
⇒ A = 450
∴ C = 120° - A = 120° - 45° = 75°
Therefore, values of angle A, B and C are 45°, 60° and 75°.
A = 45°, A = 60°, C = 75°

Question 12.
Find least positive value of x for which
tan (x + 100° ) = tan (x + 50°) tan x tan (x - 50°)
Answer:
We have
tan (x + 100°) = tan (x + 50°) tan x tan (x - 50°)

⇒ 2 sin(2x + 50°) cos(2x + 50°) = - cos 50°
⇒ sin(4x + 100°) = - cos(90° - 40°) [∵ sin 2A = 2 sin A cos A, cos(90° - θ) = sin θ]
⇒ sin (4x + 100°) = - sin 40°
⇒ sin (4x + 100°) = sin (180° + 40°)
⇒ sin (4x + 100°) = sin 220°
⇒ 4x + 100° = 220° [Since, we have to find least positive value of x]
⇒ 4x = 220° - 100°
⇒ 4x = 120°
⇒ x = 30°

Question 13.
Prove that:
cos 1° cos 2° cos 3° ....................... cos 179° = 0
Answer:
∵ cos 90° = 0
L.H.S. = cos 1° cos 2° cos 3° ..................... cos 90° ...................... cos 179° = 0
= 0 = R.H.S.
Hence Proved

Question 14.
Find the value of following trigonometric ratios:
(i) sin 135°, cos 135°, tan 135°, cot 135°, sec 135°, cosec 135°
Answer:
sin 135° = sin(90° + 45°)
= cos 45° = $\frac{1}{\sqrt{2}}$ [∵ sin (90° + θ) = cos θ]
cos 135° = cos (90° + 45°)
= - sin 45° = - $\frac{1}{\sqrt{2}}$
tan 135° = tan (90° + 45°)
= - cos 45° = - 1 [∵tan (90° + θ) = - cot θ]
cot 135° = cot (90° + 45°)
= - tan 45° = - 1 [∵cot (90° + θ) = - tan θ]

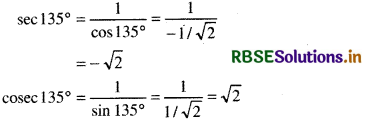
(ii) sin 150°, cos 150°, tan 150°, cot 150°, sec 150°, cosec 150°
Answer:
sin 150° = sin(90° + 60°) = cos 60° [∵ sin (90° + θ) = cos θ]

Question 15.
Find the sign of following trigonometric ratios of following angles
(i) 150°,
(ii) 230°,
(iii) 315°,
(iv) 216°.
Answer:
table - 1
Since, 150° lies in second quadrant where sin is +ve and other are negative
230° lies in third quadrant where tan is +ve and other are negative.
315° lies in fourth quadrant where cos is +ve and other are - ve .
For- 216°
sin(- 216°) = - sin 216° (∵ sin(- θ) = - sin θ)
= - sin (180° + 36°)
= - [- sin 36°] = + sin 36°
[∵ sin(180° + θ) = - sin θ]
[36° lies in first quadrant]
cos(- 216°) = cos 216°
= cos(180° + 36°)
= - cos 36° [∵ cos(180° + θ) = - cos θ]
tan(- 216°) = - tan 216° [∵ tan (- θ) = - tan θ]
= - tan (180° + 36°)
= - (tan 36°) [∵ tan(180° + θ) = tan θ]
= - tan 36°

Question 16.
Find the value of following trigonometric ratios :
(i) sin 1935°
Answer:
sin 1935° = sin 5 × 360° + 135°)
= sin 135°
=sin (90° + 45°)
[∵ sin(90° + θ) = cos θ]
= cos 45° = $\frac{1}{\sqrt{2}}$

(ii) tan 780°
Answer:
tan 780° = tan (2 × 360° + 600 )
= tan 6o° = √3

(iii) sin (- 1140°)
Answer:
sin(- 1140°) = - sin 1140°
= - sin(3 × 360° + 60°)
= sin 60° = - $\frac{\sqrt{3}}{2}$

(iv) tan (- 600°)
Answer:
tan(- 600°) = - tan(600°)
= - tan (360° + 240°)
= - tan 240°
= - tan (180° + 60°)
= - tan 60° = - √3
[∵ tan(180° + θ) = tan θ]

Question 17.
The angles of a triangle are A.P and Ratio of number of degrees in least angle and number of radians in maximum angle is 36 : π. Find angle of triangle.
Answer:
since angles of triangle are in A.P.
∴ Let angles are θ - α, θ, θ + α
∵ θ - α + θ + θ + α = 180°
or 30 = 180°
∴ θ = 60°
Maximum angles of triangle (θ + α)° = $\frac{\pi}{180^{\circ}}$(θ + α)°
We have $\frac{\theta-\alpha}{\frac{\pi}{180^{\circ}}(\theta+\alpha)}=\frac{36}{\pi}$
or $\frac{180^{\circ}(\theta-\alpha)}{(\theta+\alpha)}=\frac{36}{1}$
⇒ 5(θ - α) = θ + α
⇒ 5θ - 5α = θ + α
⇒ 5θ - θ = 5α + α
⇒ 4θ = 6α
⇒ θ = $\frac{6}{4}$α = $\frac{3}{2}$α
⇒ α = $\frac{2}{3}$ × 60° = 40°
Thus required angles are 20°, 60°, 100°.

Question 18.
Find the value of the following:
(i) cos 35° cos 25° - sin 35° sin 25°
(ii) cos A sin(A + B) - sin A cos(A + B)
Answer:
(i) cos 35° cos 25° - sin 35° sin 25°
= cos(35° + 25°) = cos 60° = $\frac{1}{2}$

(ii) cos A sin (A + B) - sin A cos (A + B)
= sin (A + B - A)
= sin B

Question 19.
Prove that:
sin 20° 28’ cos 9°32’ + cos 20° 28' sin 9°32’ = $\frac{1}{2}$.
Answer:
L.H.S. = sin 20° 28’ cos 9° 32’ + cos 20°28' A sin 9°32’
= sin (20°28’ + 9°32’)
[∵ sin A cos B + cos A sin B = sin (A + B))
= sin 30° = $\frac{1}{2}$ = R.H.S. Hence Proved

Question 20.
Prove that:
cos² 75° - cos² 15° = - $\frac{\sqrt{3}}{2}$
Answer:
L.H.S. = cos² 75° - cos² 15°
= cos² 75° - cos² (90° - 75°)
= cos² 75° - sin² 75° [∵ cos(90°- θ) = sin θ]
= cos(2 × 75°) [∵ cos 2A = cos²A - sin²A]
= cos 150°
= cos (90° + 60°) = - sin 60°
[∵ cos (90° + θ) = - sin θ]
= $\frac{-\sqrt{3}}{2}$ = R.H.S.
Hence proved

Question 21.
Prove that:
16 cos$\frac{-\sqrt{3}}{2}$ cos $\frac{4 \pi}{15}$ cos $\frac{8 \pi}{15}$ cos $\frac{14 \pi}{15}$ = 1
Answer:

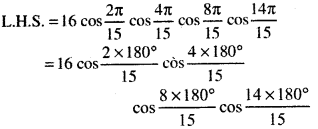
= 16 cos 24° cos 48° cos 96° c0s 168°
= 4[(2 cos 24° cos 96°) (2 c0s 48° cos 168°)]
= 4[cos(24° + 96°) + cos(24° - 96°)]
[cos(48° + 168°) + cos(48° - 168°)]
= 4[cos 120° + cos(- 72°)]
[cos 216° + cos (- 120°)]
[∵ 2cos A cos B = cos (A + B) + cos (A - B)]
= 4[cos 120° + cos 72°] [cos 216° + cos 120°] [∵ cos(- θ) = cos θ]
= 4[cos 120° + cos(90° - 18°)] [cos (180° + 36°) + cos 120°]
[cos (90 - θ) = sin θ, cos (180 + θ) = - cos θ]
= 4[cos 120° + sin 18°][- cos 36° + cos 120°]

Question 22.
Prove that:
$\left[\frac{\cos A+\cos B}{\sin A-\sin B}\right]^n+\left[\frac{\sin A+\sin B}{\cos A-\cos B}\right]^n$ = 2 cotⁿ $\left(\frac{\mathbf{A}-\mathbf{B}}{2}\right)$
where n is an even number.
Answer:
L.H.S.

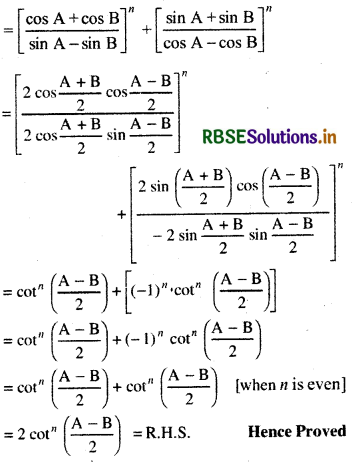
Question 23.
Prove that:
$\frac{\tan 68^{\circ}+\tan 67^{\circ}}{1-\tan 68^{\circ} \tan 67^{\circ}}$ = - 1
Answer:
L.H.S. = $\frac{\tan 68^{\circ}+\tan 67^{\circ}}{1-\tan 68^{\circ} \tan 67^{\circ}}$
= tan (68° + 67°)
[∵ tan (A + B) = $\frac{\tan A+\tan B}{1-\tan A \tan B}$]
= tan 135°
= tan (90° + 45°) [∵ tan (90 + θ) = - cot θ]
= - cot 45° = - 1
= R.H.S.
Hence Proved.

Question 24.
If α + β - γ = it then prove that sin²α + sin² β - sin²γ = 2 sin α sin β cos γ.
Answer:
LH.S. = sin²α + sin² β - sin²γ
= $\frac{1}{2}$ [2 sin²α + 2 sin² β - 2 sin²γ]
[By multiplying and divided by 2]
= $\frac{1}{2}$ [1 - cos 2α + 1 - cos 2β - (1 - c0s 2γ)]
=$\frac{1}{2}$ [1 - (cos 2α + cos 2β) + cos 2γ]
= $\frac{1}{2}$ [1 - 2 cos(α + β) cos(α - β) + 2 cos²γ - 1]
= $\frac{1}{2}$ [1 - 2 cos(π + γ) cos(α - β) + 2 cos²γ - 1] [∵ α + β - γ = π]
= $\frac{1}{2}$ [2 cos γ cos(α - β) + 2 cos² γ]
= [cos(α - β) + cos γ] cos γ
= cos (α - β) + cos[π - (α + β)] cos γ [∵ γ = α + β - π]
= [cos (α - β) - cos(α + β)] cos γ
= $\left[\frac{2 \sin (\alpha-\beta+\alpha+\beta)}{2} \sin \frac{(\alpha+\beta-\alpha+\beta)}{2}\right]$ cos γ
[∵ cos C - cos D = 2 sin $\frac{C+D}{2}$ sin $\frac{D-C}{2}$
= 2 sin α sin β cos γ
= R.H.S.
Hence Proved

Alternative Method:
L.H.S. = sin² α + sin²β - sin²γ
= sin² α + sin(β + γ).sin(β - γ)
[∵ sin² A - sin² B = sin(A + B) . sin(A - B)]
= sin² α + sin (β + γ) sin (π - α) [∵ β - γ = π - α]
= sin² α + sin (β + γ).sin α
= sin α[sin α + sin(β + γ)]
= sin α[sin (π - (β - γ)) + sin (β + γ)]
= sin α.[sin(β - γ) + sin(β + γ)] [∵ sin (π - θ) = sin θ]
= sin α . 2 sin β sin γ
= 2 sin α . 2 sin β sin γ = R.H.S.
Hence Proved

Question 25.
Prove that
$\frac{x}{1-x^2}+\frac{y}{1-y^2}+\frac{z}{1-z^2}$ = $\frac{4 x y z}{\left(1-x^2\right)\left(1-y^2\right)\left(1-z^2\right)}$
Answer:

= tan (2 × 180°) = tan 360° = 0
It is possible only when
tan 2A + tan 2B + tan 2C = tan 2A tan 2B tan 2C
= $\frac{1}{2}$ [tan 2A . tan 2B . tan 2C]

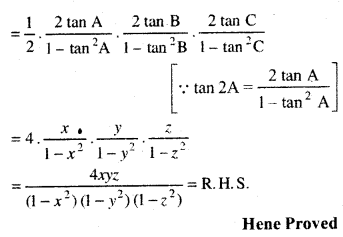
Question 26.
Write general solution of equation
4 sin⁴θ + cos⁴θ = 1
Answer:
Given equation
4 sin⁴θ + cos⁴θ = 1
Dividing both sides by cos⁴ θ
$\frac{4 \sin ^4 \theta}{\cos ^4 \theta}+\frac{\cos ^4 \theta}{\cos ^4 \theta}=\frac{1}{\cos ^4 \theta}$
⇒ 4 tan⁴θ + 1 = sec⁴ θ
⇒ 4 tan⁴θ + 1 = (1 + tan² θ)² [∵ sec²θ = 1 + tan²θ]
⇒ 4 tan⁴θ + 1 = 1 + tan⁴θ + 2 tan²θ
⇒ 3 tan⁴θ - 2 tan²θ
⇒ tan²θ[3 tan²θ - 2] = 0
⇒ tan²θ = 0 or 3 tan²θ - 2 = 0
⇒ tan θ = 0 or tan θ = ± $\sqrt{\frac{2}{3}}$
⇒ θ = nπ or θ = mπ ± tan^-1 $\sqrt{\frac{2}{3}}$
∴ θ = nπ, mπ ± tan^-1 $\sqrt{\frac{2}{3}}$n, m ∈ Z

Question 27.
Find general solution of equation
sin ⁴θ + cos⁴θ = $\frac{5}{8}$
Answer:
Given equation
sin ⁴θ + cos⁴θ = $\frac{5}{8}$
On dividing both sides by cos⁴θ
$\frac{\sin ^4 \theta}{\cos ^4 \theta}+\frac{\cos ^4 \theta}{\cos ^4 \theta}=\frac{5}{8} \times \frac{1}{\cos ^4 \theta}$
⇒ tan⁴θ + 1 = $\frac{5}{8}$ sec⁴θ
⇒ 8 tan⁴θ + 8 = 5 sec⁴θ
= 5(1 + tan² θ)² [∵ sec²θ = 1 + tan²θ]
⇒ 8 tan⁴θ + 8 = 5 (1 + tan⁴θ + 2 tan²θ)
⇒ 8 tan⁴θ + 8 = 5 + 5 tan⁴θ + 10 tan²θ)
⇒ 3 tan⁴ θ - 10 tan²θ + 3 = 0
⇒ 3 tan⁴ θ - 9 tan²θ - tan²θ + 3 = 0
⇒ 3 tan²θ (tan²θ - 3) - 1 (tan² θ - 3) = 0
⇒ (3 tan²θ - 1) (tan²θ - 3) = 0
⇒ tan²θ - 3 = 0 or 3 tan²θ - 1 = 0

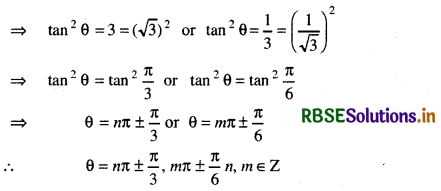
Question 28.
Find general solution of equation:
7 sin²θ + 3 cos²θ = 4
Answer:
Given equation
7 sin²θ + 3 cos²θ = 4
On dividing both sides by cos²θ
7 tan²θ + 3 = 4 sec²θ
⇒ 7 tan²θ + 3 = 4(1 + tan² θ) [∵ sec²θ = 1 + tan²θ]
⇒ 7 tan² θ + 3 = 4 + 4 tan²θ
⇒ 3 tan² θ = 4 - 3 = 1
⇒ tan² θ = $\frac{1}{3}$
⇒ tan θ = ± $\frac{1}{\sqrt{3}}$ = ± tan $\frac{\pi}{6}$
∴ θ = nπ ± $\frac{\pi}{6}$, n ∈ Z

Question 29.
Solve the equation:
sin² θ - (1 + √3) sin θ cos θ + √3 cos² θ = 0
Answer:
Dividing the equation
sin² θ - (1 + √3) sin θ cos θ + √3 cos² θ = 0 by cos² θ
tan² θ - (1 + √3)tan θ + √3 = 0
⇒ tan² θ - tan θ - √3 tan θ +√3 = 0
⇒ tan θ(tan θ - 1) - √3(tan θ - 1) = 0
⇒ (tan θ - 1) (tan θ - √3) = 0
⇒ tan θ - 1 = 0 or tan θ - √3 = θ
⇒ tan θ = 1 or tan θ = √3
⇒ tan θ = tan $\frac{\pi}{4}$ or tan θ = tan $\frac{\pi}{3}$
⇒ tan θ = 1 or tan θ = √3
⇒ tan θ = tan $\frac{\pi}{4}$ or tan θ = tan $\frac{\pi}{3}$
⇒ θ = nπ + $\frac{\pi}{4}$ or θ = mπ + $\frac{\pi}{3}$
∴ Required solution
θ = nπ + $\frac{\pi}{4}$, mπ + $\frac{\pi}{3}$ n, m ∈ Z

Question 30.
Solve the equation.
cot 2θ - cot θ + $\frac{2}{\sqrt{3}}$ = 0.
Answer:

Question 31.
Solve : sin 3θ + sin 5θ = sin 8θ
Answer:
We have
sin 3θ + sin 5θ = sin 8θ
⇒ sin 8θ - sin 5θ - sin 3θ = 0

Question 32.
Find general solution of θ which satisfies both the equations
cot θ = √3 and cosec θ = - 2
Answer:
For equation cot θ = √3
cot θ = cot 3θ°
θ = 30°
Again cot θ = √3 cot(180° + 30°)
∴ cot θ = cot 210°
θ = 210°
Thus, cot θ = √3, θ = 30°, 210°
Equation cosec θ = - 2
sin θ = - $\frac{1}{2}$ = sin (- 30°)
sin θ = - sin 30°
sin θ = sin (180° + 30°) = 210°
Again sin θ = - $\frac{1}{2}$ = - sin 30°
sin θ = sin (360° - 30°)
sin θ = sin 330°
θ = 33o°
Now, for equation cosec θ = - 2
θ = 210°, 330°
Common value of equation (i) and (ii) θ = 210° = $\frac{7 \pi}{6}$
which satisfy both the equation
∴ General value of θ = 2nπ + $\frac{7 \pi}{6}$
= (2n + 1)π + $\frac{7 \pi}{6}$

Question 33.
Find general value of angle θ which satisfies the equation cos θ = $\frac{1}{\sqrt{2}}$ and tan θ = - 1
Answer:

∴ General value of θ which satisfies both the equations is 2nπ + $\frac{7 \pi}{4}$

Question 34.
Find the value of angle θ which satisfies both the equations tan θ = - 1 and cos θ = $\frac{1}{\sqrt{2}}$
Answer:
We have
tan θ = - 1
tan θ = tan 135°
tan θ = tan (180° + 135°)
tan θ = tan 135° or tan 315°
θ = 135° or 315° ................. (i)
Again for equation cos θ = $\frac{1}{\sqrt{2}}$
cos θ = cos 45° or cos(360° - 45°)
cos θ = 45° or cos θ = 315°
θ = 45° or 315° ............ (ii)
Taking common value in equation (j) and (ii)
θ = 315° = $\frac{7 \pi}{4}$
Thus, general value of θ = 2nπ + $\frac{7 \pi}{4}$, n ∈ Z

Question 35.
If α and β satisfies the equation a cos 2θ + b sin 2θ = c then prove that:
cos²α + cos² β = $\frac{a^2+a c+b^2}{a^2+b^2}$ and cos α cos β = $\frac{a+c}{2 \sqrt{a^2+b^2}}$
Answer:
Given equation
a cos 2θ + b sin 2θ = C
⇒ b sin 2θ = c - a cos 2θ
On squaring both sides
b² sin² 2θ = c² + a² cos² 2θ - 2ac cos 2θ
b² (1 - cos² 2θ) = c² + a² . cos² 2θ - 2ac cos 2θ
b² - b² cos² 2θ = c² + a² cos² 2θ - 2ac cos 2θ
(a² + b²) cos² 2θ - 2ac cos 2θ + c² - b² = O
Given roots are α and β

Question 36.
Show that cos A - √3 sin A = 2 cos(A + $\frac{\pi}{3}$) and find maximum value of cos A - √3 sin A.
Answer:
L.H.S. = On multiplying and dividing.

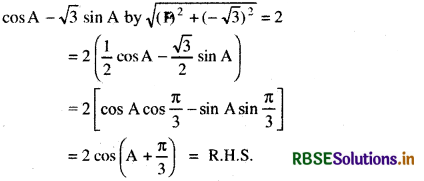
[∵ cos(C + D) = cos C cos D - sin C sin D]
Since, maximum value of cos (A + $\frac{\pi}{3}$) is 1
Thus, maximum values or expression cos A - √3 sin A is 2.

Question 37.
Find solution of equation
(1 - tan θ) (1 + tan θ)sec² θ + 2^{tan2 θ} = 0 in interval $\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$
Answer:
Given equation
(1 - tan θ) (1 + tan θ)sec² θ + 2^{tan2 θ} = 0
⇒ (1 - tan² θ) (1 + tan² θ) + 2^{tan2 θ} = 0
Putting t = tan² θ in equation
(1 - t) (1 + t) + 2' =0
or 1 - t² + 2' = 0
Equation (i) is satisfied by t = 3. since
L.H.S. = 1 - 3² + 2³
= 1 - 9 + 8 = 0 = R.H.S.
Therefore tan² θ = 3 (∵ t = tan² θ)
or tan² θ = (√3)² = tan² $\frac{\pi}{3}$
tan θ = ± tan $\frac{\pi}{3}$
∴ θ = ± $\frac{\pi}{3}, \frac{\pi}{3} \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$

Multiple Choice Questions

Question 1.
If tan θ = - $\frac{4}{3}$ then sin θ equals:
(a) - $\frac{4}{5}$
(b) - $\frac{4}{5}$ or $\frac{4}{5}$
(c) $\frac{4}{5}$
(d) None of these
Answer:
(b)   - $\frac{4}{5}$ or $\frac{4}{5}$

Question 2
If A = sin² θ + cos⁴ θ then for all real θ:
(a) 1 ≤ A ≤ 2
(b) $\frac{3}{4}$ ≤ A ≤ 1
(C) $\frac{13}{16}$ ≤ A ≤ 1
(d) None of these
Answer:
(b) $\frac{3}{4}$ ≤ A ≤ 1

Question 3.
√3 cosec 20° - sec 20° equals:
(a) 4
(b) - 4
(c) 2
(d) None of these
Answer:
(a) 4

Question 4.
(1 + cos $\frac{\pi}{8}$) (1 + cos $\frac{3 \pi}{8}$) (1 + cos $\frac{5 \pi}{8}$) (1 + cos $\frac{7 \pi}{8}$) equals:
(a) $\frac{1}{2}$
(b) $\frac{1}{8}$
(c) cos $\frac{\pi}{8}$
(d) None of these
Answer:
(b) $\frac{1}{8}$

Question 5.
If sec² θ = 2 tan θ then the value of tan²⁰¹⁵θ + cot²⁰¹⁶ θ is:
(a) 0
(b) 1
(c) 4
(d) 4031
Answer:
(c) 4

Question 6.
tan 765°equals:
(a) 1
(b) √3
(c) - √3
(d) None of these
Answer:
(a) 1

Question 7.
cos 25° cos 20° - sin 25° sin 20° equals:
(a) 0
(b) $\frac{1}{2}$
(c) $\frac{1}{\sqrt{2}}$
(d) None of these
Answer:
(c) $\frac{1}{\sqrt{2}}$

Question 8.
If α + β = $\frac{\pi}{2}$ and sin α = $\frac{1}{2}$ then β equals:
(a) $\frac{\pi}{6}$
(b) $\frac{\pi}{3}$
(c) $\frac{\pi}{4}$
(d) None of these
Answer:
(b) $\frac{\pi}{3}$

Question 9.
If cosec α = $\frac{17}{15}$ and cos β = $\frac{12}{13}$ then cos(α - β) equals:
(a) $\frac{171}{221}$
(b) $\frac{220}{221}$
(c) $\frac{221}{220}$
(d) None of these
Answer:
(a) $\frac{171}{221}$

Question 10.
sin 20° 28’ cos 90 32’ + cos 20° 28’ sin 9° 32’ equals:
(a) $\frac{1}{2}$
(b) 1
(c) - 1
(d) None of these
Answer:
(a) $\frac{1}{2}$

Question 11.
cos 20° cos 40° cos 60° cos 80° equals:
(a) $\frac{1}{8}$
(b) $\frac{1}{4}$
(c) $\frac{1}{16}$
(d) None of these
Answer:
(c) $\frac{1}{16}$

Question 12.
cos² $\frac{\pi}{8}$ + cos² $\frac{3 \pi}{8}$ + cos² $\frac{5 \pi}{8}$ + cos² $\frac{7 \pi}{8}$ equals:
(a) 1
(b) 2
(c) - 2
(d) None of these
Answer:
(b) 2

Question 13.
sin 105° + cos 105° equals:
(a) $\frac{1}{\sqrt{2}}$
(b) - $\frac{1}{\sqrt{2}}$
(c) 1
(d) None of these
Answer:
(a) $\frac{1}{\sqrt{2}}$

Question 14.
$\frac{\tan 68^{\circ}+\tan 67^{\circ}}{1-\tan 68^{\circ} \tan 67^{\circ}}$ equals:
(a) 1
(b) - 1
(c) - √3
(d) None of these
Answer:
(b) - 1

Question 15.
If sin A = $\frac{3}{5}$ then tan 2A equals:
(a) 3$\frac{3}{7}$
(b) 7$\frac{3}{5}$
(c) 3$\frac{5}{7}$
(d) None of these
Answer:
(a) 3$\frac{3}{7}$

Question 16.
If cos 30° = $\frac{\sqrt{3}}{2}$ then cos 15° equals:
(a) $\frac{1}{2} \sqrt{2+\sqrt{3}}$
(b) $\frac{1}{2} \sqrt{3+\sqrt{2}}$
(c) $\frac{1}{3} \sqrt{2+\sqrt{2}}$
(d) None of these
Answer:
(a) $\frac{1}{2} \sqrt{2+\sqrt{3}}$

Question 17.
If sin α = $\frac{1}{3}$ then sin 3α equals:
(a) $\frac{23}{27}$
(b) $\frac{25}{27}$
(c) $\frac{26}{27}$
(d) None of these
Answer:
(a) $\frac{23}{27}$

Question 18.
If $\frac{\pi}{2}$ < θ < $\frac{3 \pi}{2}$ then $\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}$ equals:
(a) sec θ - tan θ
(b) sec θ + tan θ
(c) tan θ - sec θ
(d) None of these
Answer:
(a) sec θ - tan θ

Question 19.
If x = r sin θ cos Φ, y = r sin θ sin Φ and z = r cos Φ then x² + y² + z² independent
(a) θ, Φ
(b) r, θ
(c) r, Φ
(d) None of these
Answer:
(a) θ, Φ

Question 20.
If tan θ + sec θ = √3, 0 < θ < π then value of θ is:
(a) $\frac{5 \pi}{6}$
(b) $\frac{2 \pi}{6}$
(c) $\frac{\pi}{6}$
(d) None of these
Answer:
(c) $\frac{\pi}{6}$

Question 21.
If x sin 45° cos² 60° = $\frac{\tan ^2 60^{\circ} {cosec} 30^{\circ}}{\sec 45^{\circ} \cot ^2 30^{\circ}}$ then x equals:
(a) 2
(b)4
(c) 8
(d) None of these
Answer:
(c) 8

Question 22.
The value of sin² 75° - sin² 15° is:
(a) $\frac{1}{2}$
(b) $\frac{\sqrt{3}}{2}$
(c) 0
(d) None of these
Answer:
(b) $\frac{\sqrt{3}}{2}$

Question 23.
The value of sin² 24° - sin² 6° is:
(a) $\frac{\sqrt{5}-1}{8}$
(b) $\frac{\sqrt{5}+1}{6}$
(c) $\frac{\sqrt{5}-1}{4}$
(d) None of these
Answer:
(a) $\frac{\sqrt{5}-1}{8}$

Question 24.
The value of cos² 45° - sin² 12° is:
(a) $\frac{\sqrt{5}-1}{8}$
(b) $\frac{\sqrt{5}+1}{8}$
(c) $\frac{\sqrt{5}+1}{4}$
(d) None of these
Answer:
(b) $\frac{\sqrt{5}+1}{8}$

Question 25.
The value of sin² 72° - sin² 60° is:
(a) $\frac{\sqrt{5}-1}{8}$
(b) $\frac{\sqrt{5}-1}{4}$
(c) $\frac{\sqrt{5}+1}{8}$
(d) None of these
Answer:
(a) $\frac{\sqrt{5}-1}{8}$

Question 26.
The value of sin $\frac{\pi}{10}$ + sin $\frac{13 \pi}{10}$ is:
(a) - $\frac{1}{2}$
(b) $\frac{1}{2}$
(c) 1
(d) None of these
Answer:
(a) - $\frac{1}{2}$

Question 27.
The value of sin $\frac{\pi}{10}$ sin $\frac{13 \pi}{10}$ as:
(a) - $\frac{1}{2}$
(b) $\frac{1}{2}$
(c) 1
(d) None of these
Answer:
(a) - $\frac{1}{2}$

Question 28.
The value of tan 20° tan 40° tan 60° tan 80° is
(a) 3
(b) √3
(c) $\frac{1}{\sqrt{3}}$
(d) None of these
Answer:
(a) 3

Question 29.
If cot θ = - $\frac{3}{5}$, π < θ < $\frac{3 \pi}{2}$ then value $\frac{{cosec} \theta+\cot \theta}{\sec \theta-\tan \theta}$ is:
(a) $\frac{1}{2}$
(b) 6
(c) - $\frac{1}{6}$
(d) None of these
Answer:
(a) $\frac{1}{2}$

Question 30.
If A lies in IV^th quadrant and cos A = $\frac{3}{5}$ then value of $\frac{5 \sin A+3 \sec A-3 \tan A}{4 \cot A+3 {cosec} A+5 \cos A}$.
(a) - 1
(b) 1
(c) $\frac{1}{2}$
(d) None of these
Answer:
(a) - 1

Question 31.
If sin α = $\frac{5}{13}$ and $\frac{\pi}{2}$ < α < π, then value of $\frac{\sec \alpha+\tan \alpha}{{cosec} \alpha-\cot \alpha}$ is:
(a) - 0.3
(b) 0.3
(c) $\frac{1}{3}$
(d) None of these
Answer:
(a) - 0.3

Question 32.
If sin θ = $\frac{3}{5}$, tan Φ = $\frac{1}{2}$ and $\frac{1}{2}$ < θ < π < Φ < $\frac{3 \pi}{2}$ then 8 tan θ - √5 sec Φ equals:
(a) - $\frac{7}{2}$
(b) $\frac{7}{2}$
(c) $\frac{3}{2}$
(d) None of these
Answer:
(a) - $\frac{7}{2}$

Question 33.
The value of cos 306° + cos 234° + cos 162° + cos 18° is:
(a) - 1
(b) 0
(c) 1
(d) None of these
Answer:
(c) 1

Question 34.
The value of $\frac{\sin 135^{\circ}-\cos 120^{\circ}}{\sin 135^{\circ}+\cos 120^{\circ}}$ is:
(a) 3 - 2√2
(b) 3 + 2√2
(c) 2 + 3√3
(d) None of these
Answer:
(b) 3 + 2√2

Question 35.
The value of sin (270° - θ) sin (90° + θ) - cos (270° - θ) cos (90° + θ) is:
(a) 1
(b) - 1
(c) 0
(d) None of these
Answer:
(b) - 1

Question 36.
The value of cos 24° + cos 55° + cos 125° + cos 204° + cos 300° is:
(a) - $\frac{1}{2}$
(b) $\frac{1}{2}$
(c) 1
(d) None of these
Answer:
(b) $\frac{1}{2}$

Question 37.
The value of cos A + sin (270° + A) - sin (270° - 4) + cos(180° + 4)is:
(a) - 1
(b) 0
(c) 1
(d) None of these
Answer:
(b) 0

Question 38.
The value of cos 510° cos 330° + sin 390° cos 120° is :
(a) 1
(b) - 1
(c) 0
(d) None of these
Answer:
(b) - 1

Fill in the Blanks

Question 1.
The maximum value of sin θ is .......................... .
Answer:
1

Question 2.
The general solution of sin x = $\frac{\sqrt{3}}{2}$ is ............................. .
Answer:
x = nπ + (- 1)ⁿ $\frac{\pi}{3}$

Question 3.
The greatest value of sin x cos x is .................................. .
Answer:
$\frac{1}{2}$

Question 4.
The value of $\frac{\sin 50^{\circ}}{\sin 130^{\circ}}$ is ................................ .
Answer:
- 1

Question 5.
If sin x + cos x = a, then value of sin⁶ x + cos⁶ x is ............................... .
Answer:
1 - $\frac{3\left(a^2-1\right)^2}{4}$

Question 6.
cos(A + B) = ................................
Answer:
cos A cos B - sin A sin B

Question 7.
The value of cos 12° + cos 4° + 156° + cos 132° is ....................................
Answer:
$\frac{-1}{2}$

Question 8.
The value of cos 1° cos 2° cos 3° .................................... cos 179° is ...............................
Answer:
0

Question 9.
If tan θ = 3 and θ lie in third quadrant, then the value of sin θ is ....................................
Answer:
$\frac{-3}{\sqrt{10}}$

Question 1o.
The value of sin 18° is ...................................
Answer:
$\frac{\sqrt{5-1}}{4}$

True/False

Question 1.
The value of sin 180° is 0.
Answer:
True

Question 2.
The maximum value of tan x always equal to 1.
Answer:
False

Question 3.
The value of tan $\frac{\pi}{8}$ is $\frac{\sqrt{5}-1}{4}$.
Answer:
False

Question 4.
cos 2θ = 2 cos² θ - 1
Answer:
True

Question 5.
The value of sin 50° - sin 70° + sin 10° = 0
Answer:
True

Question 6.
1 + tan² θ = sec² θ
Answer:
True

Question 7.
The principal solution of tan x = 1 is $\frac{\pi}{4}$ only.
Answer:
True

Question 8.
The value of cos x is increase in θ ∈ (0, π / 4).
Answer:
False

Question 9.
The value of tan 15° = $\frac{\sqrt{3}-1}{\sqrt{3}+1}$.
Answer:
True

Question 10.
The value of sin 18° = √5 - 1.
Answer:
False