RBSE Class 11 Maths Important Questions Chapter 2 संबंध एवं फलन

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 2 संबंध एवं फलन Important Questions and Answers.

RBSE Class 11 Maths Chapter 2 Important Questions संबंध एवं फलन

अतिलघूतरात्मक प्रश्न- 

प्रश्न 1.
समुच्चय A = {1, 2, 3, 4, 5, 6} में एक सम्बन्ध R इस प्रकार परिभाषित किया गया है कि xRy ⇔ x + 2y = 8 तो R का प्रान्त लिखिए।
हल:
दिया है- x + 2y = 8
∴ 2y = 8 - x
⇒ y = \(\frac{8-x}{2}\)
2 R3, 4R2, 6 R1
∴ R का प्रान्त = {2, 4, 6}

प्रश्न 2.
यदि A, 1 से 5 तक प्रथम पाँच प्राकृत संख्याओं का समुच्चय है और सम्बन्ध R समुच्चय A पर इस प्रकार परिभाषित है कि xRy ⇔ x < y, तो R का प्रान्त लिखिए ।
हल:
{1, 2, 3, 4}

प्रश्न 3.
A तथा B दो पृथक् समुच्चय हैं जिनमें प्रत्येक में 2 अवयव हैं, तो A से B में परिभाषित अरिक्त सम्बन्धों की संख्या ज्ञात कीजिए ।
हल:
माना A = {a, b} तथा B {x, y}
अतः A से B में अरिक्त सम्बन्ध होंगे
aRx, aRy, bRx, bRy
अतः संख्या = 4

प्रश्न 4.
यदि A = {2, 4, 9} तथा B = {-3, -2, 1, 2} तथा एक सम्बन्ध R, A से B में इस प्रकार परिभाषित हो कि - aRb ⇔ b = √a तो R को क्रमित युग्म के समुच्चय के रूप में लिखिए।
हल:
A = {2, 4, 9}, B = {-3, -2, 1, 2}

लघूत्तरात्मक प्रश्न-

प्रश्न 1.
यदि x, y ∈ { 1, 2, 3} तो निम्न में कौनसे सम्बन्ध फलन हैं-
(i) f₁ = {(x, y) : x + y > 3}
(ii) f₂ = {(x, y) : x > 3}
(iii) f₃ = {(x, y) : y = x + 1}
(iv) f₄ = {(x, y) : x + y = 4}
हल:
(i) सम्बन्ध f1 को क्रमित युग्मों के रूप में निम्न प्रकार से लिखा जा सकता है--
ƒ₁ = {(1, 3), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
यह सम्बन्ध फलन नहीं है, क्योंकि इसमें क्रमित युग्मों (2, 2) व (2, 3) के प्रथम अवयव समान हैं, इसी प्रकार क्रमित युग्मों (3, 1), (3, 2) व (3, 3) के प्रथम अवयव भी समान हैं।

(ii) सम्बन्ध f₂ को क्रमित युग्मों के रूप में निम्न प्रकार से लिख सकते हैं-
f₂ = {(2, 1), (3, 1), (3, 2)}
यह सम्बन्ध फलन नहीं है, क्योंकि 1 ∈ {1, 2, 3}, किन्तु 1 का प्रतिबिम्ब {1, 2, 3} में नहीं है।

(iii) सम्बन्ध f₃ को क्रमित रूप लिखा जा सकता है।
f₃ = {(1, 2), (2, 3)}
यह सम्बन्ध फलन नहीं है, क्योंकि 3 ∈ { 1, 2, 3}, किन्तु 3 का प्रतिबिम्ब {1, 2, 3} में नहीं है।

(iv) सम्बन्ध f4 को क्रमित रूप लिखा जा सकता है ।
f₄ = {(1, 3), (2, 2), (3, 1)}
यह सम्बन्ध फलन है, क्योंकि इसके अन्तर्गत {1, 2, 3} का प्रत्येक अवयव इसके एक अद्वितीय अवयव से सम्बन्ध है

प्रश्न 2.
निम्न फलनों को क्रमित युग्मों के रूप में व्यक्त कीजिए तथा इनके परिसर भी लिखिए-
(i) f: A → R, f(x) = x² + 1
{- 3, -2, -1, 0, 1, 2, 3}
हल:
f(x) = x² + 1
यहाँ पर x के सभी मानों को रखकर फलन को क्रमित युग्मों के रूप में निम्न प्रकार से व्यक्त किया जा सकता है-
ƒ = {(- 3, 10), (- 2, 5), (- 1, 2), (0, 1), (1, 2), (2, 5), (3, 10)}
∴ f का परिसर = {1, 2, 5, 10}

(ii) g : B → I, g(x) = x² - x
जहाँ B = {x: x ∈ N, x ≤ 5}
हल:
यहाँ पर x के सभी मानों को रखकर फलन 8 को क्रमित युग्मों के रूप में निम्न प्रकार से व्यक्त किया जाता है-
g = {(1, 0), (2, 2), (3, 6), (4, 12), (5, 20)}
∴ g का परिसर = {0, 2, 6, 12, 20}

प्रश्न 3.
यदि पूर्ण संख्याओं के समुच्चय में एक सम्बन्ध R इस प्रकार परिभाषित हो कि xRy ⇔ x² + y² = 25 तब R तथा R^-1 को क्रमित युग्मों के समुच्चय के रूप में लिखिये तथा उनके प्रान्त भी ज्ञात कीजिए।
हल:
हम देखते हैं कि xRy ⇔ x² + y² = 25
⇒ y = ± \(\sqrt{25-x^2}\)
यहाँ x = 0, ⇒ y = ± 5 ∴ (0, 5) ∈ R तथा (0, - 5) ∈ R
x = ± 3 ⇒ y = ± 4
∴ (3, 4) ∈ R, (-3, 4) ∈ R, (3, – 4) ∈ R तथा (- 3, 4) ∈ R
x = ± 4 ⇒ y = ± 3
∴ (4, 3) ∈ R, (4, - 3) ∈ R, (- 4, 3) ∈ R तथा (-4, -3) ∈ R
तथा
x = ± 5 ⇒ y = 0
∴ (5, 0) ∈ R तथा (- 5, 0) ∈ R
हम ये भी देखते हैं कि x के अन्य किसी पूर्णांकीय मान के लिये y का कोई पूर्णांकीय मान प्राप्त नहीं होता है, जो कि दिये गये सम्बन्ध को सन्तुष्ट करे ।
अतः R = {(0, 5), (0, -5), (3, 4), (-3, 4), (3, -4), (-3, -4), (4, 3), (4, -3), (-4, 3), (- 4, -3), (5, 0), (-5, 0)}
R^-1 = {(5, 0), (-5, 0), (4, 3), (4, -3), (-4, 3), (-4, -3), (3, 4), (3, -4), (3, 4), (-3, -4), (0, 5), (0, 5)}
R का प्रान्त = {0, 3, -3, 4, −4, 5, −5} = R^-1 का प्रान्त

प्रश्न 4.
यदि f: R → R, f(x) = x² हो, तो ज्ञात कीजिए-
(i) f का परिसर
(ii) {x / f (x) = 4}
(iii) {y / f(y) = -1}
हल:
(i) - f का परिसर = {x ∈ R / 0 ≤ x < ∞}
(ii) ∵ f(x) = x²
x = 2 रखने पर f(2) = (2)² = 4
x = - 2 रखने पर f (2) = (-2)² = 4
∴ {2, -2}
(iii)) Φ (ऐसा सम्भव नहीं है।)

प्रश्न 5.
यदि f: R → R निम्न प्रकार से परिभाषित हो

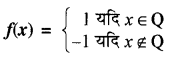
तो
(i) निम्न का मान ज्ञात कीजिए-
f\(\left(\frac{1}{2}\right)\), f(π), f(√2)
हल:

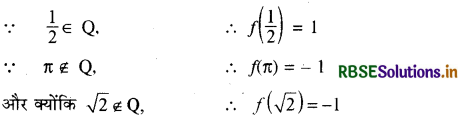
(ii) f के अन्तर्गत समुच्चय R का प्रतिबिम्ब समुच्चय निकालिये।
हल:
∵ R परिमेय तथा अपरिमेय संख्याओं का समुच्चय है
∴∀ x ∈ Q, f(x) = 1
और ∀ x ∈ Q, f(x) = - 1, जबकि x एक वास्तविक संख्या है।
अतः f के अन्तर्गत R का प्रतिबिम्ब समुच्चय (1 - 1)

(iii) 1 और - 1 के पूर्व प्रतिबिम्ब ज्ञात कीजिए।
हल:
क्योंकि 1 उन सब वास्तविक संख्याओं का प्रतिबिम्ब है जो कि Q के अवयव हैं इसलिए 1 का पूर्व - प्रतिबिम्ब समुच्चय Q होगा और इसी प्रकार 1 उन वास्तविक संख्याओं का प्रतिबिम्ब है जो कि (R - Q) के अवयव हैं इसलिए - 1 का पूर्ण - प्रतिबिम्ब समुच्चय ( R - Q) होगा।

प्रश्न 6.
वह प्रान्त ज्ञात कीजिए जिसके अन्तर्गत फलन f(x) = 2x² - 1 a g(x) = 1 - 3x आपस में बराबर हों । वह प्रान्त भी निकालिये जिसमें यह फलन आपस में बराबर नहीं हों।
हल:
दिया है f(x) = 8(x)
∴ 2x² - 1 = 1 - 3x
⇒ 2x² + 3x - 20 ⇒ (2x - 1) (x + 2) = 0
⇒ x = \(\frac{1}{2}\) या x = - 2 या दोनों।
वह प्रान्त {\(\frac{1}{2}\), -2} के लिए फलन f और फलन g बराबर होंगे।
यदि दिये गये फलन वास्तविक संख्याओं के समुच्चय R से समुच्चय R के लिए परिभाषित हों, तो फलन f और g, प्रान्त R - {\(\frac{1}{2}\), -2} के लिए बराबर नहीं होंगे।

प्रश्न 7.
यदि सम्मिश्र संख्याओं के समुच्चय C से वास्तविक संख्याओं के समुच्चय R में एक सम्बन्ध R इस प्रकार परिभाषित किया जाये कि xRy ⇔ |x| = y कारण सहित बताइये कि निम्नलिखित में से कौनसे सत्य अथवा असत्य हैं-
(i) (1 + i) R3
(iii) (2 + 3i ) R 13
(ii) 3R (-3)
(iv) (1 + i ) R1
हल:
दिया गया है किx Ry सत्य है यदि |x|

(i) यहाँ पर x = 1 + i तथा y = 3
अब |x| = |1 + i| = √(1)² + (1)² = √1 + 1 = √2
∴ | x | ≠ y अत: (1 + i ) R 3 असत्य है ।

(ii) यहाँ x = 3 तथा y = - 3
∴ |x| = 3 ≠ y अतः
3 R (-3) असत्य है|

(iii) यहाँ x = 2 + 3i तथा y = 13
∴ |x| = \(\sqrt{(2)^2+(3)^2}\) = √4 + 9 = √13
∴ |x| ≠ ? ∴ (2 + 3i) R 13 असत्य है।

(iv) यहाँ पर x = 1 + i तथा y = 1
∴ |x| = \(\sqrt{(1)^2+(1)^2}\) = √1 + 1 = √2
∴ | x | ≠ y ∴ (1 + i) R 1 असत्य है|

प्रश्न 8.
समुच्चय A = {2, 3, 4, 5} से समुच्चय B {3, 6, 7, 10} में एक सम्बन्ध R इस प्रकार परिभाषित है कि XRy ⇔ x, y के सापेक्ष अभाज्य है। सम्बन्ध R को क्रमित युग्मों के समुच्चय के रूप में लिखिए तथा R के प्रान्त एवं परिसर भी ज्ञात कीजिए।
हल:
यहाँ A = {2, 3, 4, 5} तथा B = {3, 6, 7, 10} परिभाषा के अनुसार xRy ⇔ x, y के सापेक्ष अभाज्य है ।
अतः जब x = 2 ∈ A तथा y = 3 ∈ B
तथा 2, 3 के सापेक्ष अभाज्य है अतः 2R3

अतः सम्बन्ध R = {(2, 3), (2, 7), (3, 7), (3, 10), (4, 3), (4, 7), (5, 3), (5, 6), (5, 7)}
तथा R को प्रान्त = {2, 3, 4, 5}
एवं R का परिसर
क्या = {3, 6, 7, 10}

प्रश्न 9.
क्या g = {(1, 1), (2, 3), (3, 5), (4, 7)} एक फलन है?
यदि g को g(x) = αx + β सूत्र द्वारा व्यक्त किया जाए तो α तथा β के मान ज्ञात कीजिए।
हल:
प्रश्नानुसार g = {(1, 1), (2, 3), (3, 5), (4, 7)}
यहाँ g एक फलन है क्योंकि अवयव 1, 2, 3, 4 के प्रतिबिम्ब 1, 3, 5, 7 हैं जो यह दर्शाते हैं कि प्रत्येक अवयव का एक प्रतिबिम्ब है। अतः यह एक फलन है ।
अब g(1) = 1, g(2) = 3, g (3) = 5, g(5) = 7
g (x) = αx + β से
g(1) = α.1 + β = α + β = 1 ...................... (i)
g(2) = α.1 + β = 2α + β = 3 .................... (ii)
समीकरण (ii) में से (i) को घटाने पर
2α - α = 3 - 1
या α = 2
α का मान समीकरण (i) में रखने पर
α + β = 1
α + β = 1 ⇒ β = - 1
∴ α = 2, β = - 1

प्रश्न 10.
यदि f: R → R इस प्रकार हो कि f (x) = e^x, तो ज्ञात करिये -
(i) f के अन्तर्गत R का प्रतिबिम्ब समुच्चय,
(ii) {f / f(y) = 1}
(iii) क्या f (x + y) = f(x) . f(y) सत्य है ?
हल:
(i) ∵ e^x एक वास्तविक धनात्मक संख्या है
∀ X ∈ R
∴ f(x) = e^x एक वास्तविक धनात्मक संख्या ∀ X ∈ R
प्रत्येक धनात्मक वास्तविक संख्या x के लिए
f (log x) = e^log_ex
अतः फलन f के अन्तर्गत, R का प्रतिबिम्ब समुच्चय R+ अर्थात् धनात्मक वास्तविक संख्याओं का समुच्चय होगा।

(ii) ∵ f(y) = 1
⇒ e^y = 1 = e⁰
⇒ e^y = e⁰
⇒ y = 0

(iii) ∵ f (x + y) = e^{x + y} = e^x . e^y x, y ∈ R
f(x + y) = f(x) . f(y)
∴ f(x + y) = f(x) . f(y) सत्य है।

बहुचयनात्मक प्रश्न-

प्रश्न 1.
यदि A = { a, b, c, d} तथा B = {p,g, r, s} तब A से B में सम्बन्ध है-
(A) {(a, p), (b, r), (c, r)}
(B) {(a, p), (b, q), (c, r), (s, d)}
(C) {(b, a), (q, b), (c, r)}
(D) {(c, s), (d, s), (r, a), (g, b)}
हल:
(A) {(a, p), (b, r), (c, r)}

प्रश्न 2.
N में एक सम्बन्ध R इस प्रकार परिभाषित है कि xRy ⇔ x + 4y = 16, तो R का परिसर है-
(A) {1, 2, 4)
(C) {1, 2, 3}
(B) {1, 3, 4}
(D) {2, 3, 4}
हल:
(C) {1, 2, 3}

प्रश्न 3.
N में सम्बन्ध {(1, 2), (2, 5), (3, 10), (4, 17) ......} का नियम रूप है—
(A) {(x, y) / x, y ∈ N, y = 2x + 1}
(B) {(.x, y) / x, y ∈ N, y = x² + 1}
(C) {(x, y) / x, y ∈ N, y = 3x – 1}
(D) {(x, y) / x, y ∈ N, y = 3x – 1}
हल:
(B) {(.x, y) / x, y ∈ N, y = x² + 1}

प्रश्न 4.
यदि सम्बन्ध R, "x, y का भाजक है", द्वारा परिभाषित हो तो बताइए कि N के निम्न उपसमुच्चयों में से कौनसा उपसमुच्चय एक पूर्ण क्रमित समुच्चय है-
(A) {36, 3, 9}
(C) {3, 6, 9, 12, 24}
(B) {7, 77, 11}
(D) {1, 2, 3, 4, ......}
हल:
(A) {36, 3, 9}

प्रश्न 5.
यदि A = {a, b, c} तो इसमें परिभाषित किए जाने वाले सभी सम्भव अरिक्त सम्बन्धों की संख्या है-
(A) 511
(C) 8
(B) 512
(D) 7
हल:
(A) 511

प्रश्न 6.
यदि A = {1, 2, 3, 4} तब निम्न में से कौनसा A में एक फलन है-
(A) f₁ = {(x, y) / y ' = x + 1}
(B) f₂ = {(x, y) / x + y = ≥ 4}
(C) f₃ = {(x, y) / y < x}
(D) f₄ = {(x, y) / x + y = 5}
हल:
(D) f₄ = {(x, y) / x + y = 5}

प्रश्न 7.
यदि f: R → R सन्तुष्ट करता है। f (x + y) = f(x) + f(y) सभी x, y ∈ R के लिए और f(1) = 7 तब \(\sum_{r=1}^n\) f(r) है-
(A) \(\frac{7 n}{2}\)
(B) \(\frac{7(n+1)}{2}\)
(C) 7n(n + 1)
(D) \(\frac{7 n(n+1)}{2}\)
हल:
(D) \(\frac{7 n(n+1)}{2}\)

प्रश्न 8.
निम्न में से कौनसा नियम R से R में फलन नहीं है-
(A) f(x) = x²
(B) f(x) = √x
(C) f(x) = x^1/3
(D) f(x) = x³
हल:
(B) f(x) = √x

प्रश्न 9.
यदि f(x) = \(\frac{x}{x-1}\) = y तो f(y) का मान होगा-
(A) - x
(B) x - 1
(C) x + 1
(D) x
हल:
(D) x

प्रश्न 10.
यदि A तथा B दो अरिक्त समुच्चय हैं, तब-
(A) A × B = {(a, b) : a ∈ B, b ∈ A}
(B) A × B = {(a, b) : a ∈ A, b ∈ B}
(C) A × B = {(a, b) : (a, b) ∈ A, (a, b) ∈ B}
(D) इनमें से कोई नहीं
हल:
(B) A × B = {(a, b) : a ∈ A, b ∈ B}

प्रश्न 11.
यदि f (x) = cos (log x) तो f(x) . f(y) \(\frac{1}{2}\). [f \(\left(\frac{x}{y}\right)\) + f(x . y)] बराबर है-
(A) −1
(B) 0
(C) \(\frac{1}{2}\)
(D) - 2
हल:
(B) 0

प्रश्न 12.
यदि A = {1, 2, 3, 4}, B = {2, 4, 6, 8} और A से B में एक सम्बन्ध से “x, y से बड़ा है" परिभाषित है तो R का परिसर होगा-
(A) {3, 4}
(B) {2, 6, 8}
(C) {2}
(D) {2, 4}
हल:
(C) {2}

प्रश्न 13.
यदि समुच्चय A = {2, 4, 5, 7}, B = {2, 3, 4, 6, 8} और R समुच्चय A से समुच्चय B में इस प्रकार परिभाषित है कि xRy ⇔ x, y का भाजक है तब R का परिसर होगा
(A) {2, 3, 6, 8}
(B) {2, 4, 6, 7}
(C) {2, 4, 6, 8}
(D) {4, 6, 8}
हल:
(C) {2, 4, 6, 8}

प्रश्न 14.
यदि n (A) = p, n(B) = q तो A से B में परिभाषित हो सकने वाले सम्बन्धों की संख्या होती है-
(A) 2^Pq + 1
(B) 2^{Pq - 1}
(C) 2^pq - 1
(D) 2^pq
हल:
(B) 2^{Pq - 1}

प्रश्न 15.
यदि समुच्चय C से समुच्चय R में एक सम्बन्ध Φ इस प्रकार परिभाषित है कि xΦy ⇔ |x| = y, तो सत्य कथन है-
(A) (3 + 2i) Φ 13
(B) 3Φ - 3
(C) (3 + 4i) Φ 5
(D) (1 + i) Φ R
हल:
(C) (3 + 4i) Φ 5

प्रश्न 16.
फलन f(x) = \(\frac{1}{\sqrt{|x|-x}}\) का प्रान्त है-
(A) R⁺
(B) R^-
(C) R_o
(D) R
हल:
(B) R^-

प्रश्न 17.
फलन y = √x + 1 का प्रान्त है -
(A) (-1, 0)
(B) (1, 0)
(C) (1, 0)
(D) [−1, ∞]
हल:
(D) [−1, ∞]

प्रश्न 18.
यदि f(x) = 2 |x - 2| - 3 |x - 3 | हो, तो 2 < x < 3 के लिए f (x) का मान होगा-
(A) 5 - x
(B) x - 5
(C) 5x - 13
(D) 5 + x
हल:
(C) 5x - 13

प्रश्न 19.
यदि f: R → R, f (x) = sin πx तब फलन f का परिसर होगा-
(A) {x / - π ≤ x ≤ π}
(B) {x / - 1 < x π}
(C) {x / - 1 < x < 1 }
(D) {x / - 1 ≤ x ≤ 1 }
हल:
(D) {x / - 1 ≤ x ≤ 1 }

प्रश्न 20.
फलन f(x) = cos \(\frac{x}{3}\) का परिसर है-
(A) (0, ∞)
(B) \(\left(-\frac{1}{3}, \frac{1}{3}\right)\)
(C) [−1, 1]
(D) [0, 1]
हल:
(C) [−1, 1]

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
किसी विशेष क्रम में समूहित अवयवों के युग्म को ............................................ कहते हैं।
हल:
क्रमित युग्म

प्रश्न 2.
यदि (a, b) = (x, y), तो a = ............................................ और b = ............................................
हल:
x, y

प्रश्न 3.
समुच्चय A से समुच्चय B में सम्बन्ध R कार्तीय गुणन A × B का एक ............................................ होता है।
हल:
उपसमुच्चय

प्रश्न 4.
सम्बन्ध R के क्रमित युग्मों के प्रथम घटकों का समुच्चय, सम्बन्ध R का ............................................ होता है ।
हल:
प्रान्त

प्रश्न 5.
फलन f का परिसर, f के ............................................ का समुच्चय होता है ।
हल:
प्रतिबिम्बों

प्रश्न 6.
R × R = {(x, y) | x, y ∈ R } ........................................... समतल में समस्त बिन्दुओं का समुच्चय होता है।
हल:
xy

प्रश्न 7.
यदि n(A) : = m एवं_n(B) = n तब A से B में ........................................... सम्बन्ध परिभाषित हो सकते हैं।
हल:
2^mn

प्रश्न 8.
फलन f(x) = |x| का परिसर ........................................... है ।
हल:
R⁺ ∪ {0}

प्रश्न 9.
फलन f(x) = log |xl का प्रान्त ........................................... है ।
हल:
R - {0}

प्रश्न 10.
यदि R = {(1, 2), (1, 3), (2, 3), (3, 2)} एक सम्बन्ध है तब R^-1 = ...........................................
हल:
R^-1 = {(2, 1), (3, 1), (3, 2), (2, 3)}

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
समुच्चयों A तथा B का कार्तीय गुणन समुच्चय Ax B = {(a, b) : a ∈ A; b ∈ B} होता है ।
हल:
सत्य

प्रश्न 2.
यदि n (A) = p तथा n(B) = q तो m(A × B) = 2^pq
हल:
असत्य

प्रश्न 3.
A × Φ = A
हल:
असत्य

प्रश्न 4.
किसी अवयव x का सम्बन्ध R के अन्तर्गत प्रतिबिम्ब y होता है, जहाँ (x, y) ∈ R
हल:
सत्य

प्रश्न 5.
यदि f: A → B कोई फलन है तब B फलन f का प्रान्त तथा A फलन fका सहप्रान्त होता है।
हल:
असत्य

प्रश्न 6.
किसी वास्तविक फलन के प्रान्त तथा परिसर दोनों ही वास्तविक संख्याओं का समुच्चय अथवा उसका एक उपसमुच्चय होता है ।
हल:
सत्य

प्रश्न 7.
यदि किसी समुच्चय A में n अवयव है तब A में परिभाषित सम्बन्धों की संख्या 2ⁿ² होती है
हल:
सत्य

प्रश्न 8.
यदि A = {−2, −1, 0, 1, 2} और B = {0, 1, 2, 3, 4, 5, 6} तथा f(x) = x², f: A → B तब का परिसर {0, 1} है।
हल:
असत्य

प्रश्न 9.
यदि f: X → R, f(x) = x³ + 1 तब f(9) = 730
हल:
सत्य

प्रश्न 10.
वास्तविक फलन f(x) = \(\frac{1}{x+2}\) का प्रान्त R - {-2} है।
हल:
सत्य

सही मिलान कीजिए-

भाग (A)	भांग (B)
1. फलन f(x) = \(\frac{x-1}{x-3}\)  का प्रान्त	(a) R - {1, 4}
2. फलन f(x) = \(\frac{x^2+3 x+5}{x^2-5 x+4}\)  का प्रान्त	(b) Φ
3. फलन f(x) = \(\frac{1}{\sqrt{x-5}}\) का परिसर	(c) 16
4. फलन . f(x) = \(\frac{x}{1+x^2}\)  का परिसर	(d) {-2, -1, 0, 1, 2}
5. A = {1, 2}, B = {3, 4} तब A से B में परिभाषित कुल सम्बन्ध	(e) (0, ∞)
6. यदि R = {(x, y) | x, y ∈ Z, x2 + y2 < 4}, Z में एक सम्बन्ध है, तब R का प्रान्त	(f) (0, ∞)
7. फलन f(x) = \(\frac{1}{2-\sin 3 x}\)  का प्रान्त	(g) [-½, ½]
8. फलन f(x) = \(\frac{1}{\sqrt{x-|x|}}\)  का प्रान्त	(h) R – {3}
9. फलन f(x) = \(\frac{1}{\sqrt{x+[x]}}\)  का प्रान्त	(i) [-\(\frac{1}{3}\), 1]
10. फलन f(x) = \(\frac{1}{1-2 \cos x}\)  का प्रान्त	(j) R

हल:
1. (h)
2. (a)
3. (f)
4. (g)
5. (c)
6.(d)
7. (j)
8. (b)
9. (e)
10. (i)