RBSE Class 11 Maths Important Questions Chapter 2 Relations and Functions

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 2 Relations and Functions Important Questions and Answers.

RBSE Class 11 Maths Chapter 2 Important Questions Relations and Functions

Question 1.
If f: R → R, f(x) = x², then find :
(i) Range of f,
(ii) {x |f(x) = 4},
(iii) {y |f(y) = -1}
Answer:
(i) Given, f: R → R
and f(x) = x²
then if x < 0 ⇒ x² > 0
x = 0 ⇒ x² = 0
x > 0 ⇒ x² > 0
So, f(x) = x² > 0 ∀ x ∈ R
Hence, range of R = R⁺ ∪ {0} or {x ∈ R|0 ≤ x < ∞}

(ii) f(x) = 4
⇒ x² = 4 ⇒ x = ± 2
Hence, {x : y (x) = 4} = {-2, 2}.

(iii) f(y) = - 1
⇒ y² = - 1 ⇒ y = ± y√-1 ∉ R
⇒ {y:f(y) = - 1} = Φ null set.

Question 2.
Let A = {-2, -1, 0, 1, 2} and function f is defined in A to R by f(x) = x² + 1. Find the range of f
Answer:
Given, A = {- 2, - 1, 0, 1, 2}
and R = set of real numbers
Given : f(x) = x² + 1
then f(- 2) = (- 2)² + 1 = 5
f(- 1) = (- 1)² + 1 = 2
f(0) = (0)² + 1 = 1
f(1) = (1)² + 1 = 2
f(2) = (2)² + 1 = 5
Hence, range of f = {1, 2, 5}.

Question 3.
Find domain and Range of function f which is defined by.
f(x) = \(\frac{1}{2-\cos 3 x}\)
Answer:
Given, function f(x) = \(\frac{1}{2-\cos 3 x}\)
We know that for real x, value of cos 3x lies between -1 and 1.
∴ - 1 ≤ cos 3x ≤ 1, “x ∈ R
According to definition of function
2 - cos 3x ≠ 0, “x ∈ R
∴ Function is defined for ∀ x ∈ R
∴ Domain of f = R
Again, maximum value of cos 3x is
∴ f(x) maximum value of f(x) is = 1
and minimum value of cos3x is - 1
∴ Minimum value of f(x) = \(\frac{1}{2-(-1)}\) = \(\frac{1}{3}\)
Thus, Range of f = [\(\frac{1}{3},\) 1]

Question 4.
If f: R → R is defined such that f(x) = x² + 3, then find f^-1(28) and f^-1(- 5).
Answer:
Given, f(x) = x² + 3 then f^-1 (28)
⇒ x² + 3 = 28
⇒ x² = 28 - 3 = 25
⇒ x = ±5
∴ f^-1(28) = {-5, 5)
Again f^-1(-5) → x² + 3 = - 5
⇒ x² = - 8
⇒ x = ±√-8 ∉ R
∴ f^-1 (- 5) = Φ

Question 5.
Find domain and Range of following defined functions:
(i) f(x) = sin x - cos x
(ii) f(x) = |sin x|
Answer:
(i) Given, f(x) = sin x - cos x.

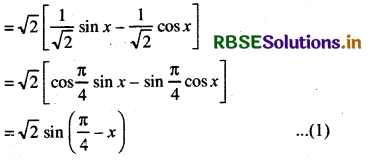
∀ x ∈ R, f(x) = √2 sin (\(\frac{\pi}{4}\) - x) is real
∴ Domain of f = R (Set of real numbers)
Again Range of sin (\(\frac{\pi}{4}\) - x) is [-1, 1]
∴ Range of f = [-√2, √2]

(ii) According to question, f(x) = |sin x|
∀ x ∈ R, value of f(x) will be real since |sin x| is real.
∴ Domain of f = R [since domain of sin x is R
∴ Domain of |sin x| will be R
We know that
⇒ 0 ≤ |sin x| ≤ 1
f(x) = Range of |sin x| = [0, 1]
[Since if sin x = - 1 then |sin x| = |- 1|= 1
and if sin x = 1 then |sin x| = |1| = 1

Question 6.
If f: R → R is defined such that f(x) = 3^x, then find (i) Range of f (ii) {x: f(x) = 1}, (iii) Is f(x + y) = f(x). f(y) true.
Answer:
(i) Since value of f(x) = 3^x is positive for all x ∈ R and for all x > 0 log₃ x ∈ R exist such that
f(log₃ x) = 3^{log 3}x = x [∵ a ^{log_a x} = x]
∴ Range of f is set of all positive real numbers

(ii) f(x) = 1
⇒ 3^x = 1
⇒ 3^x = 3⁰ ,
⇒ x = 0
∴ [x : f(x) = 1] = {0}

(iii) f(x + y) = 3^{x + y}
= 3^x . 3^y = f(x) . f(y)
∴ f(x + y) = f(x).f(y) is true for all x, y ∈ R

Question 7.
(i) If f(x) = ax² + bx + c, then find f(0), f(a), f(b)
(ii) If f(x) = x⁴ - \(\frac{1}{x^4}\), then prove that f(x) = - f\(\left(\frac{1}{x}\right)\)
(iii) If y = f(x) = \(\frac{x+2}{x-1}\), then prove that x = f(y)
Answer:
(i) We have, f(x) = ax² + bx + c then f(0) = a.0 + b.0 + c = c
f(a) = a.a² + b.a + c
= a³ + ab + c
then f(b) = a.b² + b.b + c
= ab² + b² + c

(ii) f(x) = x⁴ - \(\frac{1}{x^4}\), then

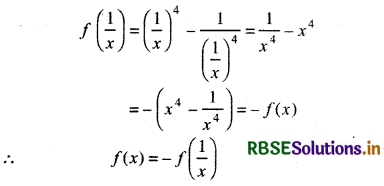
(iii) y = f(x) = \(\frac{x+2}{x-1}\)
∴ y = \(\frac{x+2}{x-1}\)
⇒ (x - 1)y = x + 2
⇒ xy - y = x + 2
⇒ xy - x = y + 2
⇒ x(y - 1) = y + 2
⇒ x = \(\frac{y+2}{y-1}\) = f(y) [∴ f(x) = \(\frac{x+2}{x-1}\)]

Question 8.
If

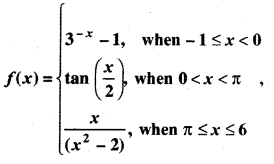
then find:
(i) f(- 1)
Answer:
f(- 1) = 3^-(-1) - 1
= 3¹ - 1 = 3 - 1 = 2
∴ f(- 1) = 2

(ii) f(π/6)
Answer:
f(π/6) = tan \(\left(\frac{\pi / 6}{2}\right)\) = tan \(\left(\frac{\pi}{12}\right)\) [∵ 0 < π / 6/ π]
= tan 15° = 2 - √3

(iii) f(2π/3)
Answer:
f\(\left(\frac{2 \pi}{3}\right)\) = tan \(\left(\frac{2 \pi}{3 \times 2}\right)\) = tan \(\frac{\pi}{3}\) [∵ 0 < 2π/3 < π]
= √3

(iv) f(4)
Answer:
f(4) = \(\frac{4}{4^2-2}=\frac{4}{16-2}=\frac{4}{14}=\frac{2}{7}\) = [∵ 0 < (4) < 6]
[∵ x lies in = 4, [π , 6]

(v) f(6)
Answer:
f(6) = \(\frac{6}{6^2-2}=\frac{6}{36-2}=\frac{6}{34}=\frac{3}{17}\) .
[∵ x lies in = 6, [π , 6]

Multiple Choice Questions

Question 1.
In the following which are functions from A to B, where A = {a, b, c} and B = {b, c, d}
(a) {(a, b)(a, d)(b, d),(c, c)}
(b) {(a,c),(b,d)}
(c) ((a, c), (b. b), (c, d)}
(d) {(a, b), (b, c), (c, b), (c, d)}.
Answer:
(c) ((a, c), (b. b), (c, d)}

Question 2.
If f:R → R is defined such that f(x) = x² then f^-1 (25) equals:
(a) 5
(b) - 5
(c) [- 5, 5]
(d) none of these
Answer:
(c) [- 5, 5]

Question 3.
If f = {(1, 2) (2, 3), (3, 4)}, then its inverse is :
(a) {(1,2), (3, 2), (4,3)}
(b) {(2,1) (3, 2), (4,3)}
(c) {(2,1), (3,2), (3,4)}
(d)None of the above
Answer:
(b) {(2,1) (3, 2), (4,3)}

Question 4.
If f:R → R is defined such that f(x) = x² then f^-1 (1, -5) equals to :
(a) 5
(b) {1,5 }
(c) Φ
(d) None of these
Answer:
(c) Φ

Question 5.
If f: R → R and g : R → R are defined such that f(x) = sin x and g(x) = x², then (gof)(x) equals to:
(a) sin x²
(b) (sin x)²
(c) x²
(d) None of the above
Answer:
(b) (sin x)²

Question 6.
If f: R → R and g : R → R is defined such that f(x) = 2x, g(x) = x² + 2, then (fog) (2) equals to:
(a) 12
(b) 11
(c) 24
(d) None of these
Answer:
(a) 12

Question 7.
If f(x) = \(\frac{2 x+3}{x-2}\); x ∈ R then \(\frac{f(10)}{f(1 / 2)}\) equals to :
(a) - \(\frac{69}{64}\)
(b) \(\frac{64}{69}\)
(c) - \(\frac{64}{69}\)
(d) None of these
Answer:
(a) - \(\frac{69}{64}\)

Question 8.
Domain of function defined by f(x) = \(\sqrt{(x-1)(3-x)}\)
(a) [1, 3]
(b) [- 3, - 1]
(c) [-3, ∞]
(d) None of these
Answer:
(a) [1, 3]

Question 9.
Domain of function defined by
f(x) = \(\frac{1}{(2 x-3)(x+1)}\)
(a) R
(b) (0, ∞)
(c) R - {-1,3 / 2}
(d) None of these
Answer:
(c) R - {-1,3 / 2}

Question 10.
If f and g are real functions defined by f (x) = x² + 7 and g(x) = 3x + 5, then value of f(3) + g(-5) equal to :
(a) 6
(b) 16
(c) 0
(d) - 10
Answer:
(a) 6

Question 11.
The range of the f(x) = \(\frac{|x|}{x}\) is equal to :
(a) {-1, 1}
(b) (- 1, 1)
(c) [-1, 1]
(d) {- 1, 0, 1}
Answer:
(a) {-1, 1}

Fill in the Blanks

Question 1.
If A and B are disjoint sets and n (4) = 2, n (B) = 3, then n(A × B) = .............................
Answer:
6

Question 2.
The domain of f(x) = √x + 7 = ................................
Answer:
[- 7, ∞]

Question 3.
If (4x + 3, y) = (3x + 5, - 2), then value of x is ..................................
Answer:
2

Question 4.
If R= {(2, 3) (\(\frac{1}{2}\), o) (2, 7) (- 4, 6)} then range of R is .............................
Answer:
{0, 3, 6, 7}

Question 5.
For any set A, A × Φ is .....................
Answer:
Φ

Question 6.
Let f(x) = x + 1, g(x) = x² + x, then value of (f + g) (x) is .............................
Answer:
x² + 2x + 1

Question 7.
The graph of an identify function always a ....................................
Answer:
straight line.

State True or False for the following statements:

Question 1.
If 4 = (1,2), then A × A × A = {(1, 1, 1) (2, 2, 2) (1, 2, 2) (2, 1, 1)}
Answer:
False

Question 2.
The order pair (5, 2) belong to the relation
R = {ix, y): y= - 5, x, y ∈ Z)
Answer:
False

Question 3.
The domain of f(x) = x² + 2 always a real number.
Answer:
True

Question 4.
For any real function f(x) co-domain of f = Range of f always.
Answer:
False

Question 5.
The range of f(x) = 1 + cos x always a real number.
Answer:
False