RBSE Class 11 Maths Important Questions Chapter 16 प्रायिकता

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 16 प्रायिकता  Important Questions and Answers.

RBSE Class 11 Maths Chapter 16 Important Questions प्रायिकता

अतिलघूत्तरात्मक प्रश्न-

प्रश्न 1.
एक रेस में भाग लेने वाले दो घोड़ों A तथा B के जीतने की प्रायिकताएँ क्रमशः \(\frac{1}{3}\) तथा \(\frac{2}{5}\) हैं, आप किस घोड़े पर दाँव लगाना पसन्द करोगे?
हल:
∵ P(A) = \(\frac{1}{3}\) = \(\frac{5}{15}\), P(B) = \(\frac{2}{5}=\frac{6}{15}\)
⇒ P(A) < P(B)
स्पष्ट है कि घोड़े B के जीतने की सम्भावना अधिक है, अत: B घोड़े पर दाँव लगाना पसन्द करेंगे।

प्रश्न 2.
एक सप्ताह में एक रविवार होने की प्रायिकता ज्ञात कीजिए।
हल:
∵ प्रत्येक सप्ताह में एक रविवार अवश्य ही होता है । अत: एक सप्ताह में एक रविवार होने की निश्चित घटना है। अतः अभीष्ट प्रायिकता = 1.

प्रश्न 3.
31 दिन वाले किसी माह में 6 रविवार होने की प्रायिकता क्या होगी ?
हल:
31 दिन वाले प्रत्येक माह में 4 सप्ताह तथा 3 दिन होंगे। 4 सप्ताह में चार रविवार निश्चित ही होंगे तथा माह में पाँच रविवार भी हो सकते हैं। यदि शेष तीन दिनों में एक दिन रविवार हो, परन्तु माह में 6 रविवार होना असम्भव घटना है।
∴ माह में 6 रविवार होना की प्रायिकता = 0

प्रश्न 4.
एक सिक्के को दो बार उछाला जाता है। दोनों बार चित आने की प्रायिकता लिखिए।
हल:
प्रायिकता = \(\frac{1}{4}\)

प्रश्न 5.
एक पासे के फेंकने पर सम अंक आने की प्रायिकता ज्ञात कीजिए। अनुकूल स्थितियाँ ( 2, 4, 6)
हल:
अनुकूल स्थितियाँ (2, 4, 6) = 3
कुल स्थितियाँ = 6
∴ अभीष्ट प्रायिकता = \(\frac{3}{6}\) = \(\frac{1}{2}\)

प्रश्न 6.
समुद्र पार जाने वाले 1000 जहाजों में से लगभग 100 जहाज डूब जाते हैं। समुद्र पार जाने वाले किसी जहाज के डूबने की प्रायिकता ज्ञात कीजिए।
हल:
यहाँ P(A) = \(\frac{m}{n}\)
प्रश्नानुसार m = 100, n = 1000
∴ P(A) = \(\frac{m}{n}\) = \(\frac{100}{1000}\) = \(\frac{1}{10}\)

प्रश्न 7.
एक ताश की गड्डी में से एक पत्ता निकाला जाता है। उस पत्ते के गुलाम होने की प्रायिकता ज्ञात कीजिए।
हल:
ताश की गड्डी में से एक पत्ता निकालने पर 4 में से एक गुलाम आने की अनुकूल स्थितियाँ = 4
∴ एक पत्ता गुलाम आने की प्रायिकता

\(\frac{4}{52}\) = \(\frac{1}{13}\)

प्रश्न 8.
10 टिकटों पर 1 से लेकर 10 तक के अंक लिखे गए हैं। एक टिकट यादृच्छया निकाला जाता है, तो उस पर लिखे अंक के 3 का गुण होने की प्रायिकता ज्ञात कीजिए।
हल:
टिकट पर लिखा अंक 1 से लेकर 10 तक कुछ भी हो सकता है।
∴ S = {1, 2, 3, 4, .................... 10} ⇒ n(S) = 10
तथा अंक के 3 गुणज होने की घटना
E = {3, 6, 9} ⇒ n(E) = 3
∴ अभीष्ट प्रायिकता P (E) = \(\frac{n(\mathrm{E})}{n(\mathrm{~S})}=\frac{3}{10}\)
[यह प्रश्न समुच्चय सिद्धान्त पर आधारित है|]

लघूत्तरात्मक प्रश्न-

प्रश्न 1.
किसी दौड़ में A के जीतने की प्रायिकता है तथा उसी दौड़ में B के जीतने की प्रायिकता है। दौड़ में किसी के भी न जीतने की प्रायिकता ज्ञात कीजिए ।
हल:
A के जीतने की प्रायिकता P(A) = \(\frac{1}{3}\) तथा
B के जीतने की प्रायिकता P (B) = \(\frac{1}{4}\)
∵ दौड़ में कोई एक ही जीत सकता है, अत: उपर्युक्त घट परस्पर अपवर्जी हैं।
∴ कम से कम किसी एक के जीतने की प्रायिकता
P(A ∪ B) = P(A) + P(B)
= \(\frac{1}{3}+\frac{1}{4}\)
∴ किसी के भी न जीतने की प्रायिकता = 1 - P(A ∪ B)
= 1 - \(\left(\frac{1}{3}+\frac{1}{4}\right)=\frac{12-7}{12}=\frac{5}{12}\)

प्रश्न 2.
4 पुरुष 3 महिलाएँ और 5 बच्चों के एक समूह में 4 व्यकि यादृच्छिक रूप से चुने जाते हैं । उनमें ठीक दो बच्चे होने क प्रायिकता ज्ञात कीजिए ।
हल:
कुल व्यक्तियों की संख्या = 4 + 3 + 5 = 12
∵ 12 व्यक्तियों में से 4 व्यक्ति ¹²C₄ तरीके से चुने जा सक हैं।
∴ कुल समप्रायिक स्थितियाँ = ¹²C₄
= \(\frac{12 \times 11 \times 10 \times 9}{1 \times 2 \times 3 \times 4}\) = 495
प्रत्येक चुनाव में 2 बच्चे होने चाहिए जिनका चयन ⁵C₂ तरीके से किया जा सकता है। 2 बच्चों के साथ शेष 2 व्यक्ति, 4 पुरुष + 3 महिलाएँ = 7 व्यक्तियों में से चुने जायेंगे जिनका चयन ⁷C₂ तरीके से किया जा सकता है ।
∴ कुल अनुकूल स्थितियाँ = ⁵C₂ × ⁷C₂
= \(\frac{5 \times 4}{1 \times 2} \times \frac{7 \times 6}{1 \times 2}\) = 210
अतः अभीष्ट प्रायिकता = \(\frac{210}{495}\) = \(\frac{14}{33}\)

प्रश्न 3.
एक थैले में 10 सफेद एवं 15 लाल गेंदें हैं तथा दूसरे थैले में 16. सफेद एवं 9 लाल गेंदें हैं। प्रत्येक थैले से एक गेंद निकाली जाती है। दोनों गेंदों के एक ही रंग के होने की प्रायिकता ज्ञात कीजिए।
हल:
पहले थैले में गेंदों की कुल संख्या = 10+ 15 = 25
दूसरे थैले में गेंदों की कुल संख्या = 16+ 9 = 25
उक्त घटना दो प्रकार से घटित हो सकती है-
(i) दोनों गेंद सफेद हों
(ii) दोनों गेंद लाल हों।
∴ पहले थैले से सफेद गेंद निकलने की प्रायिकता = \(\frac{10}{25}\)
तथा दूसरे थैले से सफेद गेंद निकालने की प्रायिकता = \(\frac{16}{25}\)
∵ दोनों घटनाएँ परस्पर स्वतंत्र हैं।
= \(\frac{10}{25} \times \frac{16}{25}=\frac{32}{125}\)
∴ दो नों गेंदों के सफेद निकलने की प्रायिकता
= \(\frac{10}{25} \times \frac{16}{25}=\frac{32}{125}\)
इसी प्रकार दोनों गेंदों के लाल होने की प्रायिकता
= \(\frac{15}{25} \times \frac{9}{25}=\frac{27}{125}\)
उक्त घटनाएँ परस्पर अपवर्जी हैं।
अतः दोनों गेंदों के एक ही रंग के होने की प्रायिकता
= \(\frac{32}{25}+\frac{27}{125}=\frac{59}{125}\)

निबन्धात्मक प्रश्न-

प्रश्न 1.
A के एक लाटरी में 3 शेयर हैं जिनमें 3 इनाम तथा 9 रिक्त हैं । B के दूसरी लाटरी में 2 इनाम तथा 6 रिक्त हैं। A तथा B के जीतने की प्रायिकताओं का अनुपात ज्ञात कीजिए।
हल:
A के जीतने की प्रायिकता-
पहली लाटरी में कुल शेयरों की संख्या = 3 इनामी + 9 रिक्त = 12
जिनमें A के 3 शेयर हैं।
12 शेयरों में से 3 शेयर चुनने के तरीके = ¹²C₃ = \(\frac{12 \times 11 \times 10}{3.2 .1}\) = 220
तथा 9 रिक्त शेयरों में से 3 शेयर चुनने के कुल तरीके = ⁹C₃
= \(\frac{9.8 .7}{3.2 .1}\) = 84
∴ A के न जीतने की प्रायिकता = \(\frac{84}{220}\) = \(\frac{21}{55}\)
तब A के जीतने की प्रायिकता = 1 - \(\frac{21}{55}\) = \(\frac{35}{55}\)

B के जीतने की प्रायिकता:
दूसरी लाटरी में कुल शेयरों की संख्या = 2 इनामी + 6 रिक्त = 8
जिनमें B के दो शेयर हैं ।
8 शेयरों में से 2 शेयर चुनने के कुल तरीके = ⁸C₂ = \(\frac{8.7}{2.1}\) = 28
6 रिक्त शेयरों में से 2 शेयर चुनने के तरीके = ⁶C₂ = \(\frac{6.5}{2.1}\) = 15
∴ B के न जीतने की प्रायिकता = \(\frac{15}{28}\)
तब B के जीतने की प्रायिकता = 1 - \(\frac{15}{28}\) = \(\frac{13}{28}\)
∴ A तथा B के जीतने की प्रायिकताओं का अनुपात
= \(\frac{\frac{34}{55}}{\frac{13}{28}}=\frac{34}{55} \times \frac{28}{13}=\frac{952}{715}\)
∴ अभीष्ट अनुपात = 952 : 715

प्रश्न 2.
यदि दो पासे फेंके जायें तो प्रायिकता क्या होगी जबकि अंकों का, योग (a) 8 से बड़ा हो (b) न 7 हो न 11
हल:
दो पासों को उछालने पर कुल स्थितियाँ 36 होंगी
(a) 8 से बड़ा योग 9, 10, 11 व 12 आ सकता है।
9 का योग आने के लिए 4 अनुकूल स्थितियाँ (3, 6), (4, 5), (5, 4), (6, 3) होंगी।
योग 9 आने की प्रायिकता (P₁) = \(\frac{4}{36}\)
10 का योग आने के लिए अनुकूल स्थितियाँ (4, 6), (5, 5), (6, 4) होंगी।
∴ योग 10 आने की प्रायिकता (P₂) = \(\frac{3}{36}\)
11 का योग आने के लिए 2 अनुकूल स्थितियाँ (5, 6), (6, 5) होंगी।
∴ योग 11 आने की प्रायिकता (P₃) = \(\frac{2}{36}\)
12 का योग आने की अनुकूल स्थितियाँ (6, 6) होंगी।
∴ योग 12 आने की प्रायिकता (P₄) = \(\frac{1}{36}\)
अब चूँकि चारों घटनाएँ अपवर्जी हैं।
अतः प्रायिकता के योग प्रमेय से
अभीष्ट प्रायिकता = P₁ + P₂ + P₃ + P₄
= \(\frac{4}{36}+\frac{3}{36}+\frac{2}{36}+\frac{1}{36}\)
\(\frac{10}{36} = \frac{5}{18}\)

(b) यहाँ 7 का योग आने के लिए 6 अनुकूल स्थितियाँ (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1) होंगी।
∴ योग 7 आने की प्रायिकता (P) = \(\frac{10}{36} = \frac{5}{18}\)
तथा 11 का योग आने के लिए 2 अनुकूल स्थितियाँ (5, 6), (6, 5) होंगी।
∴ योग 11 आने की प्रायिकता P¹ = \(\frac{2}{36}\)
∴ योग 7 या 11 आने की प्रायिकता
P + P¹ = \(\frac{6}{36}+\frac{2}{36}=\frac{8}{36}=\frac{2}{9}\)
अतः योग न 7 न 11 आने की प्रायिकता
= 1 - योग 7 या 11 आने की प्रायिकता
= 1 - \(\frac{2}{9}\) = \(\frac{7}{9}\)

प्रश्न 3.
A, 75% स्थितियों में तथा B, 80% स्थितियों में सत्य बोलते हैं, ज्ञात कीजिए कि कितने % स्थितियों में वे एक-दूसरे का विरोध करते हैं?
हल:
माना E₁ = A के सत्य बोलने की घटना
तब Ē = A के सत्य न बोलने की घटना
E₂ = B के सत्य बोलने की घटना
तब Ē₂ = B के सत्य न बोलने की घटना

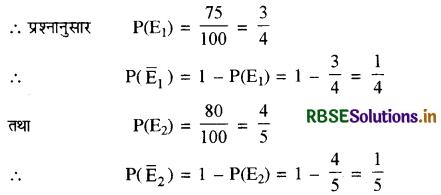
माना E = A और B द्वारा एक-दूसरे का विरोध करने की घटना । अब A और B एक-दूसरे का विरोध निम्नलिखित दो ढंगों से कर सकते हैं-
(i) A सत्य बोलता है और B सत्य नहीं बोलता है। यह घटना E₁ ∩ Ē₂ या E₁Ē₂ द्वारा व्यक्त होती है।
(ii) A सत्य नहीं बोलता है और B सत्य बोलता है। यह घटना Ē₁ ∩ E₂ या Ē₁E₂ द्वारा व्यक्त होती है।
∵ दोनों घटनाएँ परस्पर अपवर्जी हैं
⇒ P(E) = P(E₁ Ē₂) + P(Ē₁E₂)
= P(E₁) . P(Ē₂) + P( Ē₁ ) . P(E₂)
= \(\frac{3}{4} \cdot \frac{1}{5}+\frac{1}{4} \cdot \frac{4}{5}=\frac{3}{20}+\frac{4}{20}\)
= \(\frac{7}{20}\) = \(\frac{35}{100}\)
अत: 35% स्थितियों में A तथा B एक-दूसरे का विरोध करते हैं।

प्रश्न 4.
किसी घटित घटना के A, B, C तीन स्वतन्त्र गवाह हैं । A, चार बार में से तीन बार सत्य बोलता है, B, पाँच बार में से चार बार तथा C, छ: बार में से पाँच बार, तीनों गवाहों के बहुमत से घटना के पक्ष में बोलने की प्रायिकता क्या होगी ?
हल:
माना E₁, E₂, E₃ क्रमश: A, B, C के सत्य बोलने की घटना को व्यक्त करते हैं, तब

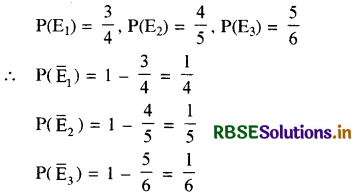
A, B, C में से कम से कम दो सत्य बोलने के लिए निम्न चार स्थितियाँ हो सकती हैं:
(i) E₁E₂E₃ (ii) E₁E₂Ē₃, (iii) E₁ Ē₂ E₃ (iv) Ē₁E₂E₃

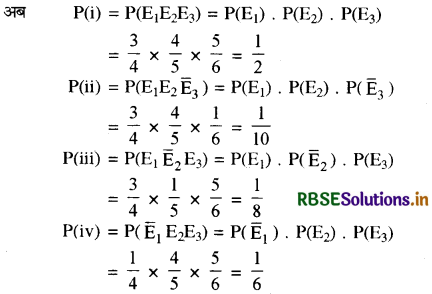
∵ चारों घटनाएँ परस्पर अपवर्जी हैं, अतः प्रायिकता के योग प्रमेय से अभीष्ट प्रायिकता
= \(\frac{1}{2}+\frac{1}{10}+\frac{1}{8}+\frac{1}{6}\) = \(\frac{107}{120}\)

प्रश्न 5.
A तथा B दो पासों को बारी-बारी से फेंकते हैं । यदि B के फेंकने से पहले A, 6 फेंकता है तो वह जीतता है और यदि A के 6 फेंकने से पहले B, 7 फेंकता है तो वह जीतता है। यदि A फेंकना प्रारम्भ करे तो सिद्ध करो कि A के जीतने की प्रायिकता \(\frac{30}{61}\) है।
हल:
दो पासों पर संख्याओं का योग 6 निम्न 5 प्रकार से आ सकता है-
(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)
अतः 6 फेंकने की प्रायिकता = \(\frac{5}{36}\)
तथा 6 न फेंकने की प्रायिकता = 1 - \(\frac{5}{36}\) = \(\frac{31}{36}\)
इसी प्रकार दो पासों पर संख्याओं का योग 7 निम्न 6 प्रकार से आ सकता है
(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
अतः 7 फेंकने की प्रायिकता = \(\frac{6}{36}\) = \(\frac{1}{6}\)
अत: 7 न फेंकने की प्रायिकता = 1 - \(\frac{1}{6}\) = \(\frac{5}{6}\)
∵ A आरम्भ करता है, अतः इसके जीतने की सम्भावनाएँ निम्नलिखित हो सकती हैं-
(i) पहले उछाल में A के 6 आवें जिसकी प्रायिकता \(\frac{5}{36}\) होगी|
(ii) पहले उछाल में A के 6 न आवें, दूसरे में B के 7 न आवें तथा तीसरे में A के 6 आवें, जिसकी प्रायिकता
\(\left(\frac{31}{36}\right) \times\left(\frac{5}{6}\right) \times\left(\frac{5}{36}\right)\) होगी।
(iii) पहले उछाल में A के 6 न आवें, दूसरे में B के 7 न आवें, तीसरे में A के 6 न आवें, चौथे में B के 7 न आवें तथा पाँचवें A के 6 आवें, जिसकी प्रायिकता

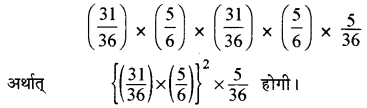
यदि यह मान लें कि A को जीतने के लिए पासों को अनन्त बार फेंकना पड़ता है, तब क्योंकि ये सभी घटनाएँ परस्पर अपवर्जी हैं, अतः प्रायिकता के योग प्रमेय से A के जीतने की प्रायिकता
= \(\frac{5}{36}+\frac{5}{36}\left\{\left(\frac{31}{36}\right) \times\left(\frac{5}{6}\right)\right\}+\frac{5}{36}\left\{\left(\frac{31}{36}\right) \times\left(\frac{5}{6}\right)\right\}^2\) + ................
उपरोक्त श्रेणी गुणोत्तर श्रेणी की अनन्त श्रेणी है। अतः गुणोत्तर श्रेणी के अनन्त पदों का योग

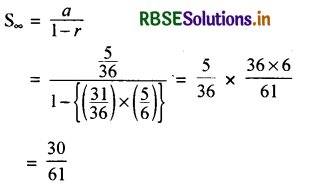
प्रश्न 6.
अगले 25 वर्षों में एक व्यक्ति के जीवित रहने की प्रायिकता 3/5 और उसकी पत्नी के उन्हीं 25 वर्षों तक जीवित रहने की प्रायिकता 2/3 है। निम्नलिखित ज्ञात कीजिए-
(1) दोनों के जीवित रहने की।
(2) किसी के भी जीवित न रहने की।
(3) कम से कम एक के जीवित रहने की।
(4) केवल पत्नी के जीवित रहने की।
हल:
अगले 25 वर्षों तक व्यक्ति के जीवित रहने की प्रायिकता

प्रश्न 7.
A और B ने शतरंज के 12 खेल खेले, जिनमें से A ने 6 खेल जीते तथा 2 खेल बराबर रहे। दोनों ने 3 खेल और खेलने का समझौता किया । प्रायिकता ज्ञात कीजिए जबकि-
(1) A ने तीन खेल जीते।
(2) दो खेल बराबर रहे।
(3) A तथा B एकान्तर रूप से जीते।
हल:

बहुचयनात्मक प्रश्न-

प्रश्न 1.
दो पासों को फेंकने पर अंकों का योग 4 का गुणज आने की प्रायिकता है-
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{9}\)
(D) \(\frac{5}{9}\)
हल:
(A) \(\frac{1}{4}\)

प्रश्न 2.
तीन पासों की फेंक में तीनों पर समान अंक आने की प्रायिकता है-
(A) \(\frac{1}{36}\)
(B) \(\frac{3}{22}\)
(C) \(\frac{1}{6}\)
(D) \(\frac{1}{18}\)
हल:
(A) \(\frac{1}{36}\)

प्रश्न 3.
एक पंक्ति में यादृच्छिक रूप से 10 विद्यार्थी बैठे हैं। दो विशेष प्रकार के विद्यार्थी पास-पास नहीं बैठने की प्रायिकता है -
(A) \(\frac{1}{5}\)
(B) \(\frac{2}{5}\)
(C) \(\frac{3}{5}\)
(D) \(\frac{4}{5}\)
हल:
(D) \(\frac{4}{5}\)

प्रश्न 4.
किन्हीं दो स्वतंत्र घटनाओं A और B के लिए P(A + B) बराबर है--
(A) P(A) + P(B) - P (AB)
(B) P(A) + P(N) - P (A). P (B)
(C) P(A) + P(B) + P(AB)
(D) P(A) + P(B)
हल:
(D) P(A) + P(B)

प्रश्न 5.
किसी निश्चित घटना की प्रायिकता होगी-
(A) 0
(B) \(\frac{1}{2}\)
(C) 1
(D) 2
हल:
(C) 1

प्रश्न 6.
एक परिवार में तीन बच्चों में से कम से कम एक लड़का हो तो उस परिवार में 2 लड़के और 1 लड़की होने की प्रायिकता है-
(A) \(\frac{1}{2}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{3}{4}\)
हल:
(B) \(\frac{1}{3}\)

प्रश्न 7.
एक अध्यापक के कक्षा में परीक्षा लेने की प्रायिकता 1/5 है। यदि एक विद्यार्थी दो बार अनुपस्थित रहे, तो उसके कम से कम एक परीक्षा नहीं दे सकने की प्रायिकता है-
(A) \(\frac{9}{25}\)
(B) \(\frac{13}{25}\)
(C) \(\frac{11}{25}\)
(D) \(\frac{23}{25}\)
हल:
(A) \(\frac{9}{25}\)

प्रश्न 8.
52 पत्तों की गड्डी में एक पत्ता खींचा जाए तो उसके राजा या ईंट का पत्ता होने की प्रायिकता है-
(A) \(\frac{1}{26}\)
(B) \(\frac{4}{13}\)
(C) \(\frac{3}{26}\)
(D) \(\frac{3}{13}\)
हल:
(B) \(\frac{4}{13}\)

प्रश्न 9
तीन सिक्कों के उछाल में कम से कम एक चित आने की प्रायिकता है
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{7}{8}\)
हल:
(D) \(\frac{7}{8}\)

प्रश्न 10.
यदि दो घटनाओं A और B के लिए P(AB) = P (A) P(B) हो, तो दोनों घटनाएँ होंगी-
(A) परस्पर अपवर्जी
(B) आश्रित
(C) स्वतंत्र
(D) उपर्युक्त में से कोई नहीं
हल:
(C) स्वतंत्र

प्रश्न 11.
बुखार की एक दवाई 75% व्यक्तियों को लाभ पहुँचाती है। यदि 3 व्यक्ति जिनको बुखार है, इसका सेवन करते हैं । उस दवाई से तीनों व्यक्तियों को लाभ पहुँचने की प्रायिकता होगी-
(A) \(\frac{27}{64}\)
(B) \(\frac{1}{64}\)
(C) \(\frac{27}{32}\)
(D) उपर्युक्त में से कोई नहीं
हल:
(A) \(\frac{27}{64}\)

प्रश्न 12.
किन्हीं दो घटनाओं A तथा B के लिए यदि P (A) = 0.4, P(A ∪ B) = 0.7 तथा P(B) = 0.3 हो, तो
(A) Ā तथा B स्वतंत्र होंगी
(B) A तथा B परस्पर अपवर्जी हैं
(C) A तथा B स्वतंत्र होंगी
(D) उपर्युक्त में से कोई नहीं
हल:
(B) A तथा B परस्पर अपवर्जी हैं

प्रश्न 13.
ताश के 52 पत्तों में से यादृच्छिक रूप से एक पत्ता चुने जाने पर उसके हुकुम का पत्ता होने की प्रायिकता है-
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{3}{4}\)
(D) \(\frac{1}{13}\)
हल:
(A) \(\frac{1}{4}\)

प्रश्न 14.
एक थैले में तीन लाल और तीन नीली गेंदें हैं। प्रथम बार एक गेंद निकाली जाती है और उस गेंद को वापस थैले में न डालते हु दूसरी गेंद निकाली जाती है। दोनों के अलग-अलग रंग होने क प्रायिकता है-
(A) \(\frac{3}{10}\)
(B) \(\frac{1}{4}\)
(C) \(\frac{3}{5}\)
(D) \(\frac{1}{2}\)
हल:
(C) \(\frac{3}{5}\)

प्रश्न 15.
किन्हीं दो घटनाओं A तथा B के लिए निम्नलिखित कौनसा सत्य है-
(A) P(A ∩ B) ≥ P(A)
(B) P(A ∩ B) = P (A) P (B)
(C) P(A ∩ B) < P(A)
(D) उपर्युक्त में से कोई नहीं
་हल:
(C) P(A ∩ B) < P(A)

प्रश्न 16.
A तथा B टेनिस के समान स्तर के अच्छे खिलाड़ी हैं। यदि उन्हें चार गेम खिलाए जाएँ तो उनमें A के ठीक तीन गेम जीतने की, प्रायिकता है-
(A) \(\frac{1}{7}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{3}{4}\)
हल:
(C) \(\frac{1}{4}\)

प्रश्न 17.
एक लीप वर्ष में 53 रविवार आने की प्रायिकता होगी-
(A) \(\frac{5}{7}\)
(B) \(\frac{1}{7}\)
(C) \(\frac{2}{7}\)
(D) \(\frac{6}{7}\)
हल:
(C) \(\frac{2}{7}\)

प्रश्न 18.
तीन पत्र और तीन लिफाफे हैं। पत्रों को लिफाफे में डालने पर केवल एक पत्र के सही लिफाफे में डालने की प्रायिकता है-
(A) \(\frac{1}{3}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{1}{6}\)
(D) \(\frac{2}{3}\)
हल:
(B) \(\frac{1}{2}\)

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
A और B परस्पर अपवर्जी घटनाएँ हैं तब A ∩ B = ................................
हल:
Φ

प्रश्न 2.
समान प्रायिकता वाले सभी परिणाम, .................................... परिणाम कहलाते हैं।
हल:
सम सम्भावित

प्रश्न 3.
प्रायिकता को प्रेक्षण और संकलित आँकड़ों के आधार पर ज्ञात करने को प्रायिकता का ........................................ दृष्टिकोण कहते हैं।
हल:
सांख्यिकीय

प्रश्न 4.
किसी यादृच्छिक परीक्षण के किसी सम्भावित नतीजे को ...................................... कहते हैं।
हल:
परिणाम

प्रश्न 5.
यदि यादृच्छिक परीक्षण के सभी सम्भावित परिणामों का समुच्चय उस परीक्षण का ................................... कहलाता है ।
हल:
प्रतिदर्श समष्टि

प्रश्न 6.
प्रतिदर्श समष्टि S का कोई उपसमुच्चय एक ............................... कही जाती है।
हल:
घटना

प्रश्न 7.
यदि किसी घटना E में केवल एक ही प्रतिदर्श बिन्दु हो, तो घटना E को .................................... घटना कहते हैं।
हल:
सरल

प्रश्न 8.
यदि किसी घटना में एक से अधिक प्रतिदर्श बिन्दु होते हैं तो उसे .................................... घटना कहते हैं।
हल:
मिश्र

प्रश्न 9.
प्रत्येक घटना A के सापेक्ष अन्य घटना A' होती है जिसे घटना A की ....................................... घटना कहते हैं।
हल:
पूरक

प्रश्न 10.
यदि E₁, E₂, ......................... E_n किसी प्रतिदर्श समष्टि S की n घटनाएँ हैं और यदि E₁ ∪ E₂ ∪ E₃ ........................ ∪ E_n = 5 तब E₁, E₂, E₃, ........................., E_n को घटनाएँ कहते हैं।
हल:
निःशेष ।

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
एक सिक्के को दो बार उछालने पर प्रतिदर्श समष्टि {HH, HT, TH, TT} है।
हल:
सत्य

प्रश्न 2.
एक सिक्के को तीन बार उछालने पर प्रतिदर्श समष्टि में 6 अवयव आते हैं।
हल:
असत्य

प्रश्न 3.
एक सिक्के को चार बार उछालने पर प्रतिदर्श समष्टि में 16 अवयव आते हैं।
हल:
सत्य

प्रश्न 4.
तीन पासों को एक साथ उछालने पर प्रतिदर्श समष्टि में कुल 215 अवयव आते हैं।
हल:
असत्य

प्रश्न 5.
यदि किसी यादृष्टिक प्रयोग से सम्बन्धित दो घटनाएँ A तथा B हों तो P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
हल:
सत्य

प्रश्न 6.
एक सिक्का दो बार उछाला जाता है तब कम से कम एक पट आने की प्रायिकता \(\frac{4}{5}\) है।
हल:
असत्य

प्रश्न 7.
किसी घटना A की प्रायिकता \(\frac{2}{11}\) है तब घटना A- नहीं की प्रायिकता \(\frac{9}{11}\) है।
हल:
सत्य

प्रश्न 8.
एक पासा फेंकने पर 6 से बड़ी संख्या आने की प्रायिकता 0 है
हल:
सत्य

प्रश्न 9.
ताश की गड्डी के 52 पत्तों में से एक पत्ता यादृच्छया निकाला गया है। पत्ते का हुकुम का इक्का होने की प्रायिकता \(\frac{1}{13}\) है।
हल:
असत्य

प्रश्न 10.
दो पासे उछालने पर, कम से कम एक पासे पर 3 से अधिक संख्या आने की प्रायिकता \(\frac{3}{4}\) है|
हल:
सत्य

सही मिलान कीजिए-

भाग (A)	भाग (B)
1. तीन सिक्के उछालने पर तीन चित आने की प्रायिकता	(a) \(\frac{1}{6}\)
2. तीन सिक्के उछालने पर न्यूनतम 2 चित आने की प्रायिकता	(b) \(\frac{6}{216}\)
3. एक पासा फेंकने पर छ: से छोटी संख्या आने की प्रायिकता	(c) \(\frac{1}{8}\)
4. दो पासे फेंकने पर आने वाले अंकों का योग 5 आने की प्रायिकता	(d) \(\frac{1}{132}\)
5. दो पासे फेंकने पर आने वाले अंकों का योग 7 आने की प्रायिकता	(e) \(\frac{1}{2}\)
6. एक थैले में 3 लाल, 4 सफेद और 5 नीली गेंदें हैं। दो गेंदें निकालने पर दोनों के भिन्न रंग की होने की प्रायिकता	(f) \(\frac{3}{7}\)
7. 6 लड़के व 6 लड़कियाँ एक पंक्ति में बैठे हैं। सभी लड़कियों के साथ बैठने की प्रायिकता	(g) \(\frac{47}{66}\)
8. दो पासों को फेंकने पर दोनों पर 1 आने की प्रायिकता	(h) \(\frac{5}{6}\)
9. एक लीप वर्ष में 53 शुक्रवार या 53 शनिवार होने की प्रायिकता	(i) \(\frac{1}{9}\)
10. तीन पासे फेंकने पर तीनों पर समान अंक आने की प्रायिकता	(j) \(\frac{1}{36}\)

हल:
1. (c)
2. (e)
3. (h)
4. (i)
5. (a)
6. (g)
7. (d)
8. (j)
9. (f)
10. (b)