RBSE Class 11 Maths Important Questions Chapter 16 Probability

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 16 Probability Questions and Answers.

RBSE Class 11 Maths Chapter 16 Important Questions Probability

Question 1.
From a well shuffled pack of 52 cards, 2 cards are drawn. Find the probability that out of the selected cards 1 is king and 1 is queen.
Answer:
Total no. of ways to draw 2 cards out of 52 cards of a pack = ⁵²C₂
No. of ways to select 1 king out of 4 = ⁴C₂
No. of ways to select 1 queen out of 4 = ⁴C₂
Thus, probability to get 1 king and 1 queen

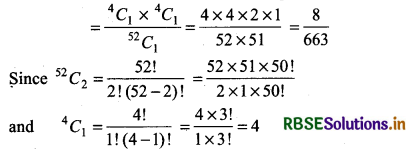
Question 2.
In a game, probability of winning of four teams are \(\frac{1}{7}\), \(\frac{1}{8}\), \(\frac{1}{9}\) and \(\frac{1}{10}\) respectively. Find the probability of not winning by any one out of these four teams.
Answer:
Probability of winning the first team = \(\frac{1}{7}\)
Probability of winning the second team = \(\frac{1}{8}\)
Probability of winning the third team = \(\frac{1}{9}\)
Probability of winning the fourth team = \(\frac{1}{10}\)
All above events are mutually exclusive (only 1 event occur at a time).
Probability of winning any team
P = \(\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{10}=\frac{1207}{2520}\)
Thus, probability of not winning any team
= 1 - p = 1 - \(\frac{1207}{2520}\) = \(\frac{1313}{2520}\)

Question 3.
In a competition of hit the target, probability of hitting the target by A and B are \(\frac{2}{5}\) and \(\frac{1}{5}\) respectively, then find the probability:
(i) both hit the target
(ii) target be hit
(iii) target cannot be hit
Answer:
We have
Probability that A hits the target = P(A) = \(\frac{2}{5}\)
Probability that B hits the target = P(B) = \(\frac{1}{5}\)
Two events are independent.
Thus, probability that both hit the target
= P(A ∩ B)
∴ P(A ∩ B) = P(A).P(B) = \(\frac{2}{5} \times \frac{1}{5}\) = \(\frac{2}{25}\)

(ii) Target. be hit means target be hit by anyone or both.
Probability of hit the target by both = \(\frac{2}{25}\) ......................... (i)

(iii) Not hit the target L e., neither A nor B hit the target Probability that A, not hit the target = 1 - P(A)
= 1 - \(\frac{2}{5}\) = \(\frac{3}{5}\) ............... (i)
Probability that B, not hit the target = 1 - \(\frac{1}{5}\) = \(\frac{4}{5}\) ......... (ii)
Thus, probability that, not hit the target = \(\frac{3}{5} \times \frac{4}{5}\)
= \(\frac{12}{25}\)

Question 4.
The probabilities of two events A and B are 0.25 and 0.50 respectively. Probability that two events A and B occur together is 0.14. Find the probability that neither event A occur nor event B.
Answer:
We have, P(A) = 0.25
P(B) = 0.50
and P(A ∩ B) = 0.14
Thus, probability that both the events occur
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
= 0.25 + 0.50 - 0.14 = 0.61
Probability that ‘both the events not occur’.
P(A’ ∩ B’) = P(A ∪ B)’ = 1 - P(A ∪ B)
= 1 - 0.61 = 0.39

Question 5.
Three dice are thrown altogether. Find the probability to get sum at least 6.
Answer:
In throwing three dice altogether, all possible results are = 6 × 6 × 6 = 216
IfS be sample space, then
n(S) = 216
Let A = Event ‘at least sum 6 appear’
then A’ = Event ‘appear sum less than 6’
= Event to appear 3 or 4 or 5
= {(1, 1, 1); (1, 1, 2), (1, 2, 1), (2, 1, 1), (1, 1, 3) (1, 3, 1), (3, 1, 1), (1, 2, 2), (2, 1, 2), (2, 2, 1)}
∴ n(A') = 10

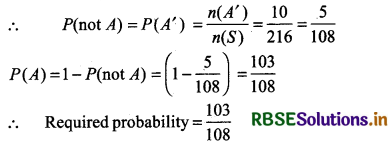
Question 6.
Two dice are thrown together. Find the
probability to get odd digit on first dice or sum 8.
Answer:
In throwing two dice, number of elements in
sample space S will be 36.
i.e., n(S) = 36
Let E₁ = Event to get odd digit on first dice
E₂ = Event to get sum 8 on two dice
then E₁ = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
and E₂ = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
∴ n(E₁) = 18 and n(E₂) = 5
E₁ ∩ E₂ = {(3, 6), (5, 3)}
∴ n(E₁ ∩ E₂) = 2

Question 7.
It is possible that a student got A, B, C or D grade. Find the probability that he could got at least B grade whereas probability to get A grade is 0.20, probability to got B grade is 0.40 and of C grade is 0.30, and of D grade is 0.10.
Answer:
Probability to get at least B grade = Probability to get A grade + Probability to get B grade
= 0.20 + 0.40 = 0.60

Question 8.
If four coins are tossed altogether, then find the probability to get at least 1 tail.
Answer:
In tossing 4 coins altogether, number of elements
in sample space = 4² = 16
∴ P(at least 1 tail) = (1 Tail or 2 Tails or 3 Tails)
= 1 - P (0 Tail)
= 1 - P {HHHH}
= 1 - \(\frac{1}{16}\) = \(\frac{15}{16}\)

Question 9.
From a well shuffled pack of cards one card is drawn. Find the probability that selected card be king or heart card.
Answer:
Number of cards in a pack of cards = 52
∴ n(S) = 52
Let A = Event to appear king card, n(A) = 4
B = Event to apear heart card, n(B) = 13

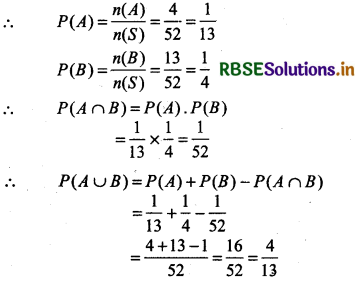
Question 10.
From a well shuffled pack of 52 cards, 5 cards are drawn. Find the probability that in drawn cards, 3 of heart and 2 of flower.
Answer:
Total no. of ways to draw 5 cards out of a pack of card = ⁵²C₅
∴ No. of elements in sample space S = ⁵²C₅
i.e.. n(S) = ⁵²C₅
Since, there are 13 heart cards and 13 flower cards in a pack of cards.
∴ Total no. of ways to draw 3 heart cards out of a pack of cards = ¹³C₃
Total no. of ways to draw 2 flower cards out of a pack of cards = ⁴³C₂.
∴ Total no. of ways to draw 3 heart and 2 flower cards
out of a pack of cards = ¹³C₃ × ¹³C₂
Let E = Event to draw 3 heart and 2 flower cards out of a pack of cards
Then, n(E) = ¹³C₃ × ¹³C₂
∵ Probability of event E

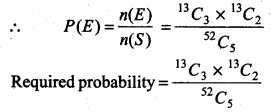
Question 11.
From a group of 7 males and 3 females a committee of 6 persons has to be formed. Find the probability that committee contain exactly two females.
Answer:
Total number of persons = 7 + 4 = 11
∴ No. of elements in sample sapce S
= No. of ways to select 6 persons out of a group of 11 persons = ¹¹C₆
∴ n(S) = ¹¹C₆
Total no. of ways to select 4 males out of 7 males = ⁷C₄
Total no. of ways to select 2 females out of 4 females = ⁴C₂
Let E = Event to select 2 females and 4 males out of 7
∴ n(E) = ⁷C₄ × ⁴C₂
∴ Required probability

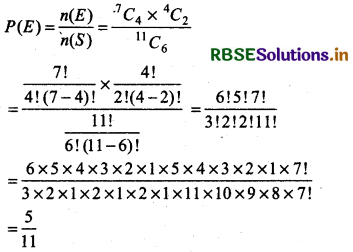
Question 12.
From 400 natural numbers, I natural number is selected. Find the probability that selected number is divisible by 2 or 5.
Answer:
Let S be sample space, then n(S) = 400
Again, let E₁ = Event ‘number divisible by 2’
E₂ = Event ‘number divisible by 5’
∴ E₁ ∩ E₂ = Event ‘number divisible by 2 or 5’
= Event ‘number divisible by 10’
E₁ = {2, 4, 8, 10, 12, 14, .............. 398, 400)
E₂ = {10, 20, 30, ... 390, 400)
∴ E₁ ∩ E₂ = {10, 20, 30, ..., 390, 400)

Then, P (selected number is divisible by 2 or 5)
= P(E₁ or E₂) - P(E₁ ∪ E₂)
⇒ P(E₁ ∪ E₂) = P(E₁) + P(E₂) - P(E₁ ∩ E₂)
⇒ P(E₁ ∪ E₂) = \(\frac{1}{2}+\frac{1}{5}-\frac{1}{10}=\frac{5+2-1}{10}=\frac{6}{10}=\frac{3}{5}\)
Required probability = \(\frac{3}{5}\)

Question 13.
25 Tickets are numbered from 1 to 25. One ticket is randomly chosen. Find the probability that number marked on ticket be multiple of 2 or 5.
Answer:
Let sample space be S.
E₁ = Event ‘number marked on selected ticket is multiple of 2 or 5’
E₂ = Event ‘number marked on selected ticket in multiple of 5’
∴ E₁ ∪ E₂ = Event ‘number marked on selected ticket is divisible by 2 or 5’
and E₁ ∩ E₂ = Event ‘number marked on selected ticket is divisible by 2 and 5.
Now, S = {1, 2, 3, 4, ....... 25} .
E₁ = {2, 4, 6, 8, ... 24}
E₂ = {5, 10,15, 20, 25)
∴ n(S) = 25, n(E₁) = 12, n(E₂) = 5
E₁ ∩ E₂ = {10, 20), n(E₁ ∩ E₂) = 2

Multiple Choice Questions

Question 1.
Two dice are thrown together. What is the probability to get odd digit on first dice or sum 8 on two dice:
(a) \(\frac{7}{12}\)
(b) \(\frac{5}{12}\)
(c) \(\frac{5}{12}\)
(d) None of these
Answer:
(a) \(\frac{7}{12}\)

Question 2.
In a random throw of a die, probability to get a specific number is:
(a) \(\frac{1}{6}\)
(b) \(\frac{5}{6}\)
(c) 1
(d) None of these
Answer:
(a) \(\frac{1}{6}\)

Question 3.
In throwing a die, probability to get digit less than 4 is:
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{4}\)
(d) None of these
Answer:
(a) \(\frac{1}{2}\)

Question 4.
In throwing a die, probability to get odd digit is:
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{4}\)
(d) None of these
Answer:
(a) \(\frac{1}{2}\)

Question 5.
Four coins are tossed together. Probability to get at least one tail is:
(a) \(\frac{15}{16}\)
(b) \(\frac{13}{16}\)
(c) \(\frac{11}{16}\)
(d) None of these
Answer:
(a) \(\frac{15}{16}\)

Question 6.
A coin is tossed 3 times, then probability to get head on all three coins is:
(a) \(\frac{1}{8}\)
(b) \(\frac{3}{8}\)
(c) \(\frac{5}{8}\)
(d) None of these
Answer:
(a) \(\frac{1}{8}\)

Question 7.
A bag contains 5 red colour, 4 green colour and 6 black colour balls. One ball is randomly drawn from the bag. Probability that the drawn ball is of red colour is:
(a) \(\frac{2}{3}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{4}{5}\)
(d) None of these
Answer:
(b) \(\frac{1}{3}\)

Question 8.
A bag contains 10 red, 20 blue and 30 green balls. 5 balls are drawn from the bag. Probability that all drawn balls are blue is:
(a) \(\frac{{ }^{60} C_5}{{ }^{20} C_5}\)
(b) \(\frac{{ }^{20} C_5}{{ }^{60} C_5}\)
(c) \(\frac{{ }^{20} C_5}{{ }^{60} C_{20}}\)
(d) None of these
Answer:
(b) \(\frac{{ }^{20} C_5}{{ }^{60} C_5}\)

Question 9.
A bag contains 8 white and 4 red balls 5 balls are drawn from the bag. Probability that 2 red and 3 white balls are drawn, is:
(a) \(\frac{15}{33}\)
(b) \(\frac{14}{33}\)
(c) \(\frac{15}{13}\)
(d) None of these
Answer:
(b) \(\frac{14}{33}\)

Question 10.
A bag contains 5 white and 7 black balls. 1 ball is randomly drawn. Probability that drawn ball is of red colour, is:
(a) \(\frac{5}{12}\)
(b) \(\frac{7}{12}\)
(c) \(\frac{3}{7}\)
(d) None of these
Answer:
(b) \(\frac{7}{12}\)

Question 11.
A bag contains 9 red,7 white and 4 black balls. 1 ball is randomly drawn. Probability that the drawn ball is of red or black colour is:
(a) \(\frac{11}{20}\)
(b) \(\frac{13}{20}\)
(c) \(\frac{9}{20}\)
(d) None of these
Answer:
(b) \(\frac{13}{20}\)

Question 12.
A bag contains 3 white, 7 red and 15 black balls and another bag contains 10 white, 6 red and 9 black balls. Probability to get red ball from I bag and white ball from II bag is:
(a) \(\frac{13}{125}\)
(b) \(\frac{14}{125}\)
(c) \(\frac{17}{125}\)
(d) None of these
Answer:
(b) \(\frac{14}{125}\)

Question 13.
From a well shuffled pack of 52 cards, one card is randomly chosen. Probability that chosen card is heart, is:
(a) \(\frac{4}{13}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{5}{13}\)
(d) None of these
Answer:
(b) \(\frac{1}{4}\)

Question 14.
A card is randomly chosen from a well shuffled pack of cards. Probability that the drawn card is not ace is:
(a) \(\frac{1}{13}\)
(b) \(\frac{12}{13}\)
(c) \(\frac{5}{13}\)
(d) None of these
Answer:
(b) \(\frac{12}{13}\)