RBSE Class 11 Maths Important Questions Chapter 15 सांख्यिकी

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 15 सांख्यिकी  Important Questions and Answers.

RBSE Class 11 Maths Chapter 15 Important Questions सांख्यिकी

अतिलघूत्तरात्मक प्रश्न-

प्रश्न 1.
निम्न बारम्बारता बंटन का परास ज्ञात कीजिए-

हल:
सबसे छोटा वर्ग (10 - 20) है तथा इसकी निम्न सीमा = 10 है।
अत: न्यूनतम मूल्य (L) = 10
सबसे बड़े वर्ग 50 - 60 की उपरिसीमा = 60 है।
अतः अधिकतम मूल्य (H) = 60
∴ परास (R) = H - L = 60 - 10 = 50

प्रश्न 2.
मानक विचलन की परिभाषा लिखिए ।
हल:
श्रेणी के विभिन्न चर मूल्यों के समान्तर माध्य से प्राप्त विचलन के वर्गों के समान्तर माध्य के वर्गमूल को मानक विचलन कहते हैं।
मानक विचलन (σ) = \(\sqrt{\sum_{i=1}^n \frac{\left(x_i-\bar{x}\right)^2}{n}}\)

प्रश्न 3.
यदि किसी श्रृंखला के सभी मदों का मूल्य एकसमान हो, तो विक्षेपण का मान ज्ञात कीजिए।
हल:
सभी मदों का मूल्य एकसमान होने पर विक्षेपण = () (शून्य)।

प्रश्न 4.
व्यक्तिगत श्रृंखला में मानक विचलन ज्ञात करने का सूत्र लिखिए ।
हल:
σ = \(\sqrt{\frac{\sum_{i=1}^n x_i^2}{n}-\left(\frac{\sum_{i=1}^n x_i}{n}\right)^2}\)

प्रश्न 5.
किसी बंटन का मानक विचलन 20.5 तथा समान्तर माध्य 60 हो, तो उसका मानक विचलन गुणांक ज्ञात कीजिए ।
हल:
मानक विचलन गुणांक

= \(\frac{20.5}{60}\)
= 0.34

प्रश्न 6.
विक्षेपण से आप क्या समझते हैं? उसके कौन-कौनसे माप हैं ?
हल:
विक्षेपण (Dispersion ) - किसी श्रेणी के पदों का माध्य से बिखराव विक्षेपण कहलाता है। किसी श्रेणी का विक्षेपण उसके विभिन्न पदों के विचरण (variation) या अन्तर का माप है। विक्षेपण के माप दो प्रकार के होते हैं—
(i) निरपेक्ष माप (Absolute measure)
(ii) सापेक्ष माप (Relative measure)

प्रश्न 7.
माध्यिका से लिया गया माध्य विचलन अन्य किसी मान से लिये गये माध्य विचलन से छोटा होता है या बड़ा ? लिखिए ।
हल:
छोटा ।

प्रश्न 8.
मानक विचलन पर मूल बिन्दु के परिवर्तन का क्या प्रभाव पड़ता है?
हल:
कोई प्रभाव नहीं पड़ता है।

प्रश्न 9.
यदि किसी बंटन का प्रसरण 16.81 है, तो उसका मानक विचलन लिखिए।
हल:
मानक विचलन = √प्रसरण
= √16.81
= 4.1

प्रश्न 10.
यदि किसी बंटन का मानक विचलन σ तथा समान्तर माध्य हो, तो उसका मानक विचलन गुणांक लिखिए।
हल:
मानक विचलन गुणांक = \(\frac{\sigma}{\bar{x}}\)

प्रश्न 11.
किसी बंटन में समान्तर माध्य से लिये विचलनों का योग लिखिए।
हल:
विचलनों का योग शून्य होता है।

प्रश्न 12.
यदि किसी बंटन का मानक विचलन 15.4 तथा समान्तर माध्य 120.2 हो, तो उसका विचरण गुणांक लिखिए ।
हल:
विचरण गुणांक = \(\frac{\sigma}{\bar{x}}\) × 100
= \(\frac{15.4}{120.2}\) × 100
= 12.81%

प्रश्न 13.
माध्य विचलन की परिभाषा दीजिए तथा इसके दो गुण लिखिए।
हल:
किसी भी श्रेणी में चर के विभिन्न मानों का, उसके सांख्यिकी माध्य ( समान्तर माध्य, माध्यिका एवं बहुलक) से लिए विचलनों के निरपेक्ष मानों का समान्तर माध्य उसका माध्य विचलन कहलाता है । गुण: (i) यह सभी आँकड़ों पर आधारित होता है। यदि किसी भी आँकड़े का मान बदल जाता है तो माध्य विचलन का मान भी बदल जाता है।
(ii) यह माप परिकलन व समझने में आसान है।

प्रश्न 14.
वर्गीकृत बारम्बारता बंटन के लिए माध्यिका ज्ञात करने का सूत्र लिखिए।
हल:
माध्यिका (M) = l + \(\frac{\frac{\mathrm{N}}{2}-\mathrm{C}}{f}\) × h

प्रश्न 15.
150 मदों का माध्य 90 है और मानक विचलन 6 है। मदों का योग और मदों के वर्गों का योग ज्ञात कीजिए ।
हल:
मदों का योग = मदों की संख्या × उनका माध्य
= 150 × 90 = 13500
यहाँ x̄ = 90, n = 150, मानक विचलन (σ) = 6

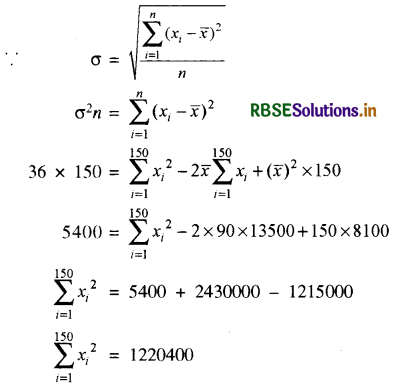
प्रश्न 16.
25 संख्याओं का मानक विचलन 40 है। यदि प्रत्येक संख्या को 5 बढ़ाया गया है तब नया मानक विचलन ज्ञात करो ।
हल:
यदि सभी पद एक निश्चित अचर द्वारा बढ़ाया या घटाया जाए तो मानक विचलन पूर्ववत रहेगा अर्थात् अभीष्ट मानक विचलन 40 है।

लघूत्तरात्मक प्रश्न-

प्रश्न 1.
चार विद्यार्थियों के प्राप्तांक निम्न हैं- 25, 35, 45, 55 तो माध्य से माध्य विचलन ज्ञात कीजिए।
हल:
यहाँ समान्तर माध्य x̄ = \(\frac{\Sigma x_i}{\mathrm{~N}}\)
= \(\frac{25+35+45+55}{4}\)
= \(\frac{160}{4}\) = 40

S.No	xi	|xi – 40|
1.	25	15
2.	35	5
3.	45	5
4.	55	15
	कुल Σ |xi – 40| = 40

∴ समान्तर माध्य से विचलन = \(\frac{1}{n}\) Σ |x_i - 40| = \(\frac{40}{4}\)
= 10

प्रश्न 2.
एक कक्षा के 9 छात्रों के भार (किग्रा. में ) निम्न प्रकार हैं- 47, 50, 58, 45, 53, 59, 47, 60, 49 तथा इसकी माध्यिका 50 है तो माध्यिका से लिया गया माध्य विचलन ज्ञात कीजिए।
हल:
यहाँ M = 50

S.No	xi	|xi – 50|
1.	47	3
2.	50	0
3.	58	8
4.	45	5
5.	53	3
6.	59	9
7.	47	3
8.	60	10
9.	49	1
	कुल Σ |xi – 50| = 42

∴ माध्यिका से माध्य विचलन = \(\frac{1}{n}\) Σ |x_i - 50|
= \(\frac{42}{9}\) = 4.67

प्रश्न 3.
10 मैचों में खिलाड़ी द्वारा बनाए गए रनों की संख्या निम्न है -
38, 70, 48, 34, 42, 55, 63, 46, 54, 44
प्रसरण तथा मानक विचलन ज्ञात कीजिए।
हल:
समान्तर माध्य
x̄ = \(\frac{38+70+48+34+42+55+63+46+54+44}{10}\)
= \(\frac{494}{10}\) = 49.4

xi	(xi - x̄)	(xi – x̄)2
38	-11.4	129.96
70	+20.6	424.36
48	-1.4	1.96
34	-15.4	237.16
42	-7.4	54.76
55	+5.6	31.36
63	+13.6	184.96
46	-3.4	11.56
54	+4.6	21.16
44	-5.4	29.16
		Σ (xi – x̄)2 = 1126.4

∴ प्रसरण σ² = \(\frac{1}{n}\) Σ (x_i - x̄)²
σ² = \(\frac{1126.4}{10}\) = 112.64
तथा मानक विचलन σ = + √σ² = √112.64
= 10.61

प्रश्न 4.
2n प्रेक्षणों की एक श्रेणी में, आधे a के बराबर तथा शेष आधे - a के बराबर हैं। यदि प्रेक्षणों का मानक विचलन 2 है तब |a| का मान ज्ञात करो।
हल:
माना a, a, a, ........ n बार एवं - a, - a - a, ........... n बार तक अर्थात् माध्य = 0

निबन्धात्मक प्रश्न-

प्रश्न 1.
एक महाविद्यालय के विद्यार्थियों के एक प्रतिरूपी समूह की गर्दनों के नाप पर आधारित निम्न आँकड़े हैं-

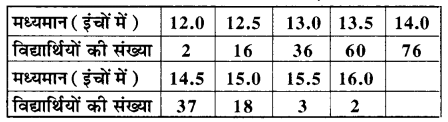
उपर्युक्त का माध्य तथा मानक विचलन की गणना कीजिए।
हल:
माना यहाँ कल्पित माध्य = 14

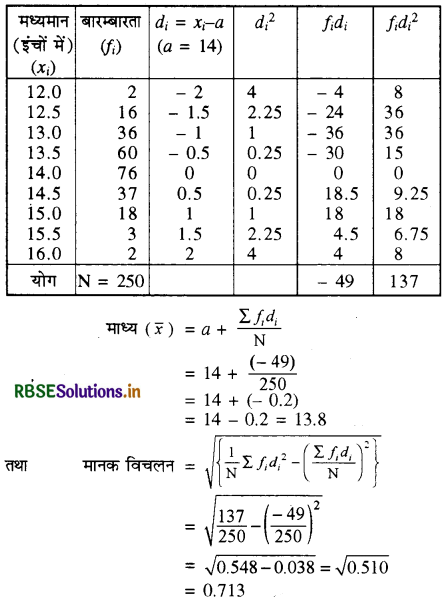
प्रश्न 2.
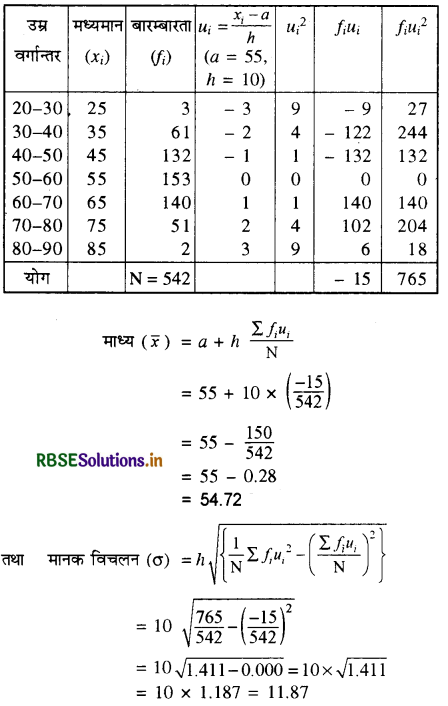
542 व्यक्तियों की निम्न सारणी में दिये हुए उम्र के बंटन का माध्य एवं मानक विचलन ज्ञात कीजिए-

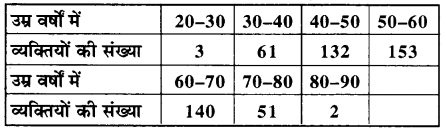
हल:
यहाँ माना कल्पित माध्य = 55

प्रश्न 3.
100 परिवारों की आय का बारम्बारता बंटन निम्न प्रकार है-

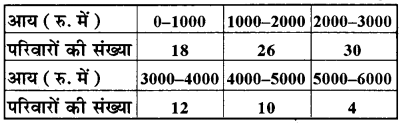
मानक विचलन ज्ञात कीजिए ।
हल:
माना कल्पित माध्य a = 3500
वर्ग अन्तराल h = 1000

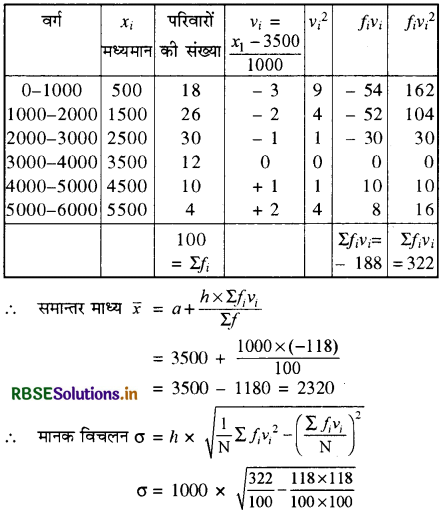
σ = 1000 × \(\sqrt{\frac{32200-13924}{100 \times 100}}\)
σ = 10√18276 = 10 × 1351.88
σ = 1351.88
अतः मानक विचलन σ = 1351.88

प्रश्न 4.
एक सत्र में लिए गए 10 टेस्टों में दो छात्रों A और B के प्राप्तांक इस प्रकार हैं-

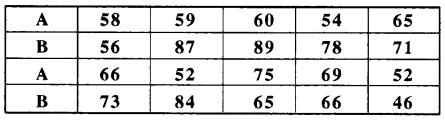
दोनों छात्रों में से कौनसा छात्र अधिक संगत (consistent) है?
हल:
हम यहाँ पर छात्र A तथा B के अलग-अलग मानक विचलन ज्ञात करेंगे-
छात्र A के लिए-
समान्तर माध्य = \(\frac{\sum x}{n}\)
= \(\frac{58+59+60+54+65+66+52+75+69+52}{10}\)
समान्तर माध्य x̄ = \(\frac{610}{10}\) = 61
अब हम इसका मानक विचलन निकालेंगे-

xi	(xi - x̄)	(xi – x̄)2
58	-3	9
59	-2	4
60	-1	1
54	-7	49
65	+4	16
66	+5	25
52	-9	81
75	+14	196
69	+8	64
52	-9	81
		Σ (xi – x̄)2 = 526

अतः मानक विचलन = \(\sqrt{\frac{\sum\left(x_i-\bar{x}\right)^2}{n}}\)
= \(\sqrt{\frac{526}{10}}\) = √52.6 = 7.25

छात्र B के लिए:
समान्तर माध्य x̄ = \(\frac{\sum x}{n}\)
x̄ = \(\frac{56+87+89+78+71+73+84+65+66+46}{10}\)
= \(\frac{715}{10}\) = 71.5

xi	(xi - x̄)	(xi – x̄)2
58	-15.5	240.25
59	+15.5	240.25
60	+17.5	306.25
54	6.5	42.25
65	-0.5	0.25
66	+1.5	2.25
52	+12.5	156.25
75	-6.5	42.25
69	-5.5	30.25
52	-25.5	650.25
		Σ (xi – x̄)2 = 1710.25

अतः मानक विचलन = \(\sqrt{\frac{\sum\left(x_i-\bar{x}\right)^2}{n}}\)
= \(\sqrt{\frac{1710.5}{10}}\) = √171.05 = 17.68
अतः छात्र A अधिक संगत है। चूँकि इसके मानक विचलन का मान कम है।

प्रश्न 5.
श्रेणी, a + d, a + 2d, ........, a + 2nd के माध्य से माध्य विचलन तथा मानक विचलन ज्ञात कीजिए और सिद्ध कीजिए कि परिवर्ती पहले वाले से बड़ा है।
हल:
दी गई श्रेणी a, a + d, a + 2d, ............... a + 2nd समान्तर श्रेणी है। अतः

यहाँ पर भी वह स्थिति पैदा हो रही है जो कि उपर्युक्त मा विचलन में हुई थी । हम उपर्युक्त व्यंजक को इस प्रकार भी लिर सकते हैं-
σ = \(\sqrt{\frac{2 d^2\left\{1^2+2^2+3^2+4^2+\ldots \ldots+n^2\right\}}{(2 n+1)}}\)
लेकिन हम जानते हैं कि समान्तर श्रेणी से (1² + 2² + 3² + 4² + ................. + n² का मान \(\frac{n(n+1)(2 n+1)}{6}\) होता है।
मान रखने पर -
σ = \(\sqrt{\frac{2 d^2(n)(n+1)(2 n+1)}{6 \times(2 n+1)}}\)
σ = d\(\sqrt{\frac{n(n+1)}{3}}\) ...................... (2)
समीकरण (1) तथा समीकरण (2) से स्पष्ट है कि परिवर्ती पहले वा से बड़ा है|

बहुचयनात्मक प्रश्न-

प्रश्न 1.
पाँच छात्रों के सांख्यिकी में प्राप्तांक 20, 35, 25, 30 तथा 15 हैं तो इसका परास होगा-
(A) 15
(B) 20
(C) 25
(D) 30
हल:
(B) 20

प्रश्न 2.
किसी चर श्रेणी का समान्तर माध्य x̄ = 773 व माध्य विचलन 64.4 है तो उसका माध्य विचलन गुणांक होगा-
(A) 0.083
(B) 0.073
(C) 0.065
(D) 12.003
हल:
(A) 0.083

प्रश्न 3.
आँकड़ों 6, 10, 4, 7, 4, 5 का मानक विचलन है-
(A) \(\sqrt{\frac{13}{3}}\)
(B) \(\frac{13}{3}\)
(C) √26
(D) \(\frac{\sqrt{26}}{6}\)
हल:
(A) \(\sqrt{\frac{13}{3}}\)

प्रश्न 4.
एक कक्षा के छात्रों के प्राप्तांकों का मानक विचलन 1.6 है तो बंटन का प्रसरण होगा-
(A) 1.6
(B) 0.4
(C) 2.56
(D) (2.56)²
हल:
(C) 2.56

प्रश्न 5.
यदि मानक विचलन σ = \(\sqrt{\frac{\sum f d^2}{\mathrm{~N}}-\left(\frac{\sum f d}{30}\right)^2}\) है, तो N का मान है-
(A) 10
(B) 30
(C) 15
(D) 20
हल:
(B) 30

प्रश्न 6.
एक श्रेणी का विचरण गुणांक 30% है तथा मानक विचलन 15 है, तो उसका माध्य है-
(A) 5
(B) 5
(C) 50
(D) 2
हल:
C) 50

प्रश्न 7.
किसी श्रेणी में Σx² = 100, n = 5 तथा Σx = 20 तो प्रसरण होगा-
(A) 16
(B) 4
(C) 50
(D) 2
हल:
(B) 4

प्रश्न 8.
किसी बंटन का समान्तर माध्य x̄ है, तो उसका माध्य विचलन होगा-
(A) \(\frac{\sum f_i\left(x_i-\bar{x}\right)}{\mathrm{N}}\)
(B) Σf_i |x_i - x̄|
(C) \(\frac{\sum f_i\left|\left(x_i-\bar{x}\right)\right|}{\mathrm{N}}\)
(D) \(\frac{\sum f_i\left|x_i-\bar{x}\right|^2}{\mathrm{~N}}\)
हल:
(C) \(\frac{\sum f_i\left|\left(x_i-\bar{x}\right)\right|}{\mathrm{N}}\)

प्रश्न 9.
एक कक्षा में छात्रों के प्राप्तांकों का प्रसरण 2.56 है, तो इस बंटन का मानक विचलन है-
(A) 2.56
(B) 1.6
(C) \(\frac{1}{2.56}\)
(D) (2.56)²
हल:
(B) 1.6

प्रश्न 10.
यदि आँकड़ों के किसी समूह में समान्तर माध्य से विचलनों के निरपेक्ष मानों का योग 256 और पदों की संख्या 4 है, तो माध्य विचलन है-
(A) 8
(B) 1024
(C) 64
(D) 16
हल:
(C) 64

प्रश्न 11.
यदि किसी बंटन का कल्पित माध्य a तथा समान्तर माध्य हो, तो उसका मानक विचलन होगा-

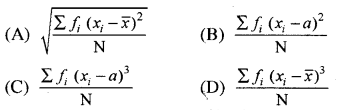
हल:
(A) \(\sqrt{\frac{\sum f_i\left(x_i-\bar{x}\right)^2}{\mathrm{~N}}}\)

प्रश्न 12.
एक वेतन का विचरण गुणांक 60 है और उनका मानक विचलन 21 है, उसका माध्य क्या होगा-
(A) 2.0
(B) 25
(C) 30
(D) 35
हल:
(D) 35

प्रश्न 13.
यदि आँकड़ों के किसी समूह में समान्तर माध्य से विचलनों के वर्गों का योग 605 और पदों की संख्या 5 है, तो मानक विचलन होगा-
(A) 10
(B) 2
(C) 11
(D) 5
हल:
(C) 11

प्रश्न 14.
यदि किसी बंटन का प्रसरण 16 तथा माध्य 25 हो तो मानक विचलन गुणांक है-
(A) 6.4
(B) 64
(C) 1.6
(D) 16
हल:
(C) 1.6

प्रश्न 15.
6, 10, 4, 7, x और 5 का माध्य 6 हो, तो x का मान होगा-
(A) 5
(B) 32
(C) 36
(D) 4
हल:
(D) 4

प्रश्न 16.
यदि किसी बंटन का कल्पित माध्य a तथा समान्तर माध्य x̄ हो, तो उसका प्रसरण है-

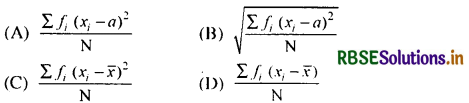
हल:
(C) \(\frac{\sum f_i\left(x_i-\bar{x}\right)^2}{\mathrm{~N}}\)

प्रश्न 17.
यदि A वह माध्य है जिससे माध्य विचलन लिया गया है, माध्य विचलन गुणांक होता है-

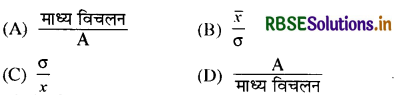
हल:

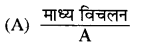
प्रश्न 18.
यदि किसी बंटन की माध्यिका 8 तथा माध्यिका से माध्य विचलन 64.8 है, तो माध्य विचलन गुणांक होगा-
(A) 8.1
(B) 81
(C) 810
(D) 8.1
हल:
(A) 8.1

प्रश्न 19.
विचरण गुणांक होता है-
(A) \(\frac{100}{\sigma} \) × x̄
(B) \(\frac{\sigma}{\bar{x}}\) × 100
(C) \(\frac{\bar{x}}{\sigma}\) × 100
(D) \(\frac{\sigma \times \bar{x}}{100}\)
हल:
(B) \(\frac{\sigma}{\bar{x}}\) × 100

प्रश्न 20.
यदि कोई श्रेणी 5-10, 10-15, 15-20, 20-25, 25-30, 30-35 के वर्गों में विभाजित है तो श्रेणी का परास होगा-
(A) 5
(B) 30
(C) 35
(D) 10
हल:
(B) 30

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
आँकड़ों में प्रकीर्णन का माप प्रेक्षणों व वहाँ प्रयुक्त ............................. की माप के आधार पर किया जाता है।
हल:
केन्द्रीय प्रकृति

प्रश्न 2.
चतुर्थक विचलन, ....................................... की एक माप है।
हल:
प्रकीर्णन

प्रश्न 3.
प्रेक्षण x का स्थिर मान a से अन्तर (x - a) प्रेक्षण x का a से .................................. कहलाता है।
हल:
विचलन

प्रश्न 4.
स्थिर संख्या 'a' से विचलनों के निरपेक्ष मानों का माध्य, ....................................... कहलाता है।
हल:
माध्य विचलन

प्रश्न 5.
M.D. (a) = ...............................
हल:
\(\frac{\sum\left|x_i-a\right|}{n}\)

प्रश्न 6.
आँकड़ों को दो प्रकार से वर्गीकृत किया जाता है- (i) ........................... (ii) ...........................
हल:
असतत बारम्बारता बंटन, सतत बारम्बारता बंटन

प्रश्न 7.
माध्य से विचलनों के वर्गों का माध्य ..................................... कहलाता है।
हल:
प्रसरण

प्रश्न 8.
विचरण गुणांक (C.V.) = ..............................
हल:
\(\frac{\pi}{x}\) × 100

प्रश्न 9.
बहुत अधिक विचरण या बिखराव वाली श्रृंखलाओं में ...................................... केन्द्रीय प्रवृत्ति की उपयुक्त माप नहीं है।
हल:
माध्यिका

प्रश्न 10.
माध्य से विचलनों का योग, माध्यिका से विचलनों के योग से .................................... होता है।
हल:
अधिक

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
माध्य, माध्यिका और बहुलक केन्द्रीय प्रवृत्ति की तीन माप हैं ।
हल:
सत्य

प्रश्न 2.
मानक विचलन प्रकीर्णन की एक माप नहीं है ।
हल:
असत्य

प्रश्न 3.
एक श्रृंखला का परिसर = अधिकतम माप – न्यूनतम माप ।
हल:
सत्य

प्रश्न 4.
माध्य विचलन, केन्द्रीय प्रवृत्ति की किसी भी माप से ज्ञात किया जा सकता है।
हल:
सत्य

प्रश्न 5.
दो श्रृंखलाओं में विचरण की तुलना के लिए प्रत्येक श्रृंखला का विचरण गुणांक ज्ञात करने की आवश्यकता नहीं होती।
हल:
असत्य

सही मिलान कीजिए-

भाग (A)	भांग (B)
1. विचरण गुणांक (C.V.)	(a) \(\frac{1}{n}\) Σfi(xi - x̄)2
2. वर्गीकृत आँकड़ों का माध्य M.D. (x̄)	(b) \(\frac{\sigma}{x}\) × 100, x̄ ≠ 0
3. अवर्गीकृत आँकड़ों का प्रसरण (σ2)	(c) \(\frac{1}{\mathrm{~N}} \sqrt{\mathrm{N} \sum f i x_i^2-\left(\sum f_i \cdot x_i\right)^2}\)
4. असतत बारम्बारता बंटन का मानक विचलन	(d) \(\frac{\sum f_i\left|x_i-\bar{x}\right|}{\mathrm{N}}\)
5. सतत बारम्बारता बंटन का मानक विचलन	(e) \(\frac{h}{\mathrm{~N}^2}\) [NΣfiyi2 – (Σfiyi)2] जहाँ yi = \(\frac{x_i-\mathrm{A}}{h}\)\(\frac{h}{\mathrm{~N}^2}\)
6. प्रसरण ज्ञात करने की लघु विधि	(f) \(\sqrt{\frac{1}{\mathrm{~N}} \sum f_i\left(x_i-\bar{x}\right)^2}\)

हल:
1. (b)
2. (d)
3. (a)
4. (1)
5. (c)
6. (e)