RBSE Class 11 Maths Important Questions Chapter 15 Statistics

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 15 Statistics Questions and Answers.

RBSE Class 11 Maths Chapter 15 Important Questions Statistics

Question 1.
The variance of 25 observations is 4 and if each observation is multiplied by 3, find the new variance of the resulting observations.
Answer:
Let the observations be x₁, x₂, x₃, ......., x_n andi be
their mean.
Given, variance = 4 and n = 25

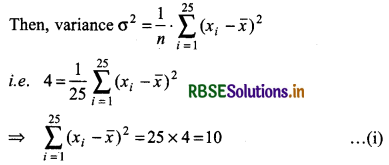
If each observation is multiplied by 3 and the new resulting observations are y_i.

Here, we see that by multiplying each observations by 3, the variance of the resulting observations becomes 3² times the original variance.

Question 2.
The variance of 20 observations is 5. If each observation is divided by 2, then find the new variance of the resulting observations.
Answer:
Let the observations be x₁, x₂, ........, x_n and x̄ be their mean.
Given, variance =5 and n = 20

Here, we see that by dividing each observation by 2, the variance of the resulting observations become \(\frac{1}{4}\) times the original variance.
Thus, variance of new observations = \(\sum_{i=1}^{20} \frac{\left(y_i-\bar{y}\right)^2}{N}\)
= \(\frac{400}{20}\) = 20 = 2² × 5 . [∵ 5 × \(\frac{1}{4}\) = \(\frac{5}{4}\)]
Here, we see that by multiplying each observation by 2, the variance of the resulting observations become 2² times the original variance.

Question 3.
Prove that variance of n observations remain unchanged If any definite number is added or subtracted to them.
Answer:
Let x₁, x₁, .........., x_n be observations and x̄ be their mean
Then their variance = σ₁² = \(\frac{1}{n} \sum_{i=1}^n\) (x_i - x̄)
If ‘a’ is added in each observation, then new observations will be y₁, y₂, ............................ y_n
where y₁ = x₁ + a, y₂ - x₂ + a, .......... y_n = x_n +a
i.e., y_i = x_i + a .......................... (i)

Thus, variance of new observations is same as the variance of original observations.

Question 4.
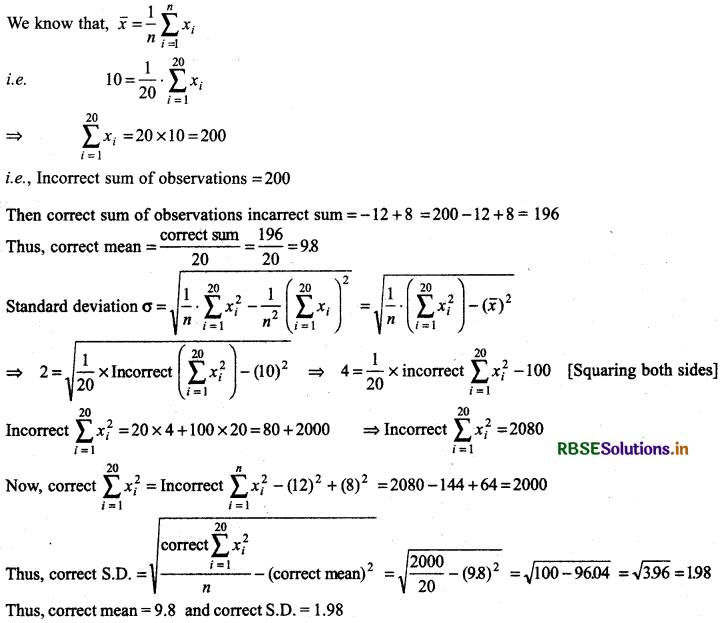
The mean of 20 observations is 10 and their standard deviation is 2. If by mistake 12 Is taken instead of observations 8, then find the correct mean and standard deviation.
Answer:
We have,
No. of observations (n) = 20
Incorrect mean (x̄) = 10
Incorrect standard deviation (σ) = 2

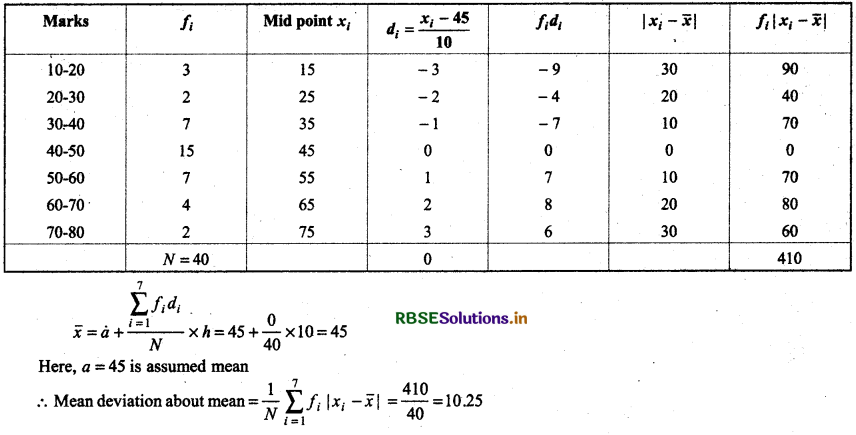
Question 5.
Find mean deviation about mean for the following data by short-cut method:
Answer:
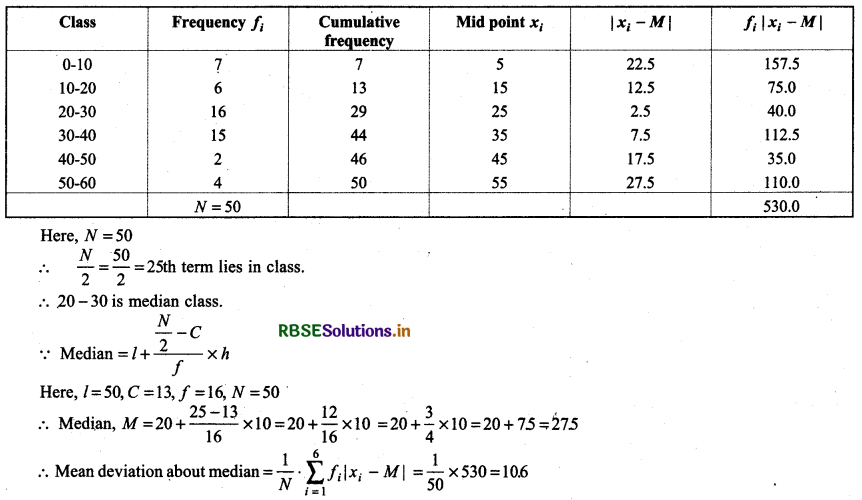
Question 6.
Find mean deviation about median for the following data.
Answer:
Question 7.
A student found mean and standard deviation of 25 observations as 56 and 2 respectively, whereas, by mistake he has taken one observation as 64. Then find correct mean and standard deviation. If Incorrect observation is removed.
Answer:
No. of observations n = 25
Incorrect mean (x̄) = 56
Incorrect standard deviation = 2
∴ Correct sum of observations Σx = nx̄ - 64 = 25 × 56 - 64 = 1336

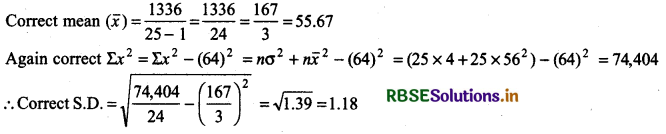
Multiple Choice Questions

Question 1.
Formula of mean deviation about mean (x̄) of observations x₁, x₂, ........................ x_n:
(a) \(\frac{1}{n} \cdot \sum_{i=1}^n\) |x_i - x̄|
(b) \(\sum_{i=1}^n\) (x_i - x̄)²
(c) \(\sqrt{\frac{\left(x_i-\bar{x}\right)^2}{n}}\)
(d) None of these
Answer:
(a) \(\frac{1}{n} \cdot \sum_{i=1}^n\) |x_i - x̄|

Question 2.
Formula of mean deviation about median (M) of observations x₁, x₂, ............................... x_n:
(a) \(\frac{1}{n} \sum_{i=1}^n\) |x_i - M|
(b) \(\frac{1}{n} \sum_{i=1}^n\) |x_i - M|²
(c) \(\frac{1}{M} \sqrt{\left(x_i-M\right)}\)
(d) None of these
Answer:
(a) \(\frac{1}{n} \sum_{i=1}^n\) |x_i - M|

Question 3.
Mean deviation about mean of observations 6, 7, 10, 12, 13, 4, 8, 12:
(a) 2.75
(b) 2.57
(c) 7.25
(d) None of these
Answer:
(a) 2.75

Question 4.
Mean deviation about median of 3, 9, 5, 3, 12, 10, 18, 4, 7, 19, 21:
(a) 5.27
(b) 5.72
(c) 7.52
(d) None of these
Answer:
(a) 5.27

Question 5.
Formula of mean variance of observations x₁, x₂, x₃, ....................., x_n:
(a) σ² = \(\frac{1}{n} \sum_{i=1}^n\) (x_i - x̄)²
(b) σ² = \(\sum_{i=1}^n\) (x_i - x̄)²
(c) σ² = \(\frac{1}{n} \sqrt{\left(x_i-\bar{x}\right)^2}\)
(d) None of these
Answer:
(a) σ² = \(\frac{1}{n} \sum_{i=1}^n\) (x_i - x̄)²

Question 6.
Formula of standard deviation of observations x₁, x₂, x₃, ........................., x_n:
(a) σ = \(\sqrt{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2}\)
(b) σ = \(\sum_{i=1}^n\) (x_i - x̄)²
(c) σ = \(\frac{\sum x_i}{n}\)
(d) None of these
Answer:
(a) σ = \(\sqrt{\frac{1}{n} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2}\)

Question 7.
If x : x₁, x₂, ................. x_n, f : f₁, f₂, ..............., f_n, then formula of standard deviation is:
(a) σ = \(\sqrt{\frac{1}{n} \sum_{i=1}^n f_i\left|x_i-\bar{x}\right|^2}\)
(b) σ = \(\sqrt{\frac{1}{n} \sum_{i=1}^n\left|x_i-\bar{x}\right|^n}\)
(c) σ = \(\sqrt{\Sigma f_i\left|x_i-\bar{x}\right|^2}\)
(d) None of these
Answer:
(a) σ = \(\sqrt{\frac{1}{n} \sum_{i=1}^n f_i\left|x_i-\bar{x}\right|^2}\)

Question 8.
Standard deviation of the following data is:

(a) 6.12
(b) 6.21
(c) 2.16
(d) None of these
Answer:
(a) 6.12

Question 9.
Variance of first n natural numbers is:
(a) \(\frac{n^2-1}{12}\)
(b) \(\frac{n^2+1}{12}\)
(c) \(\frac{(n+1)}{12}\)
(d) None of these
Answer:
(a) \(\frac{n^2-1}{12}\)

Question 10.
If coefficient of variation of any observation is 70 and standard deviation is 16, then its mean is:
(a) 22.85
(b) 22.58
(c) 2.258
(d) None of these
Answer:
(a) 22.85

Question 11.
If mean of any observation is 35 and its coefficient of variation is 60, then its standard deviation is:
(a) 21
(b) 12
(c) 6
(d) None of these
Answer:
(a) 21

Question 12.
The sum of squares of deviations about mean of 10 observations is 2.5, then its standard deviations is:
(a) 0.5
(b) 25
(c) 50
(d) None of these
Answer:
(a) 0.5

Question 13.
The variance of 20 observations is 5. If each observation is multiplied by 2, then variance of each observation is:
(a) 20
(b) 25
(c) 50
(d) None of these
Answer:
(a) 20

Question 14.
If each observation x₁, x₂, ................... x_n is exceeds by ‘a’ where a is any positive or negative number, then obtained variance is
(a) Unchanged
(b) Changed
(c) Square of first variance
(d) None of these
Answer:
(a) Unchanged

Question 15.
If variance of n observations x₁, x₂, ............. x_n is σ², then variance of observations ax₁, ax₂, ax₃, ...... ax_n is:
(a) a²σ²
(b) aσ²
(c) \(\frac{1}{a^2}\)σ²
(d) None of these
Answer:
(a) a²σ²

Fill in the Blanks

Question 1.
...................................... deals with data collected for specific purpose.
Answer:
statistics

Question 2.
Mean is obtained by ....................................... the sum of the observations by the number of observations.
Answer:
dividing

Question 3.
The dispersion or scatter in a data is measured on the basis of the .....................................
Answer:
observations

Question 4.
The difference of maximum and minimum values of series is called ....................................
Answer:
range

Question 5.
The mean of the absolute values of the deviations from the central value is called mean ......................................
Answer:
devaiation

Question 6.
While calculating the mean of a continuous frequency distribution, the frequency in each class is centered at its .........................................
Answer:
mid-point

Question 7.
In short cut method, the deviations of the observations are taken from the ........................................ mean.
Answer:
assumed

Question 8.
It there is a common factor of all the deviations, then ..................................... them by this common factor to further simplify the deviations.
Answer:
divide

Question 9.
In a series, where the degree of ................................... is very high, the median is not a representation central tendency.
Answer:
variability

Question 10.
The sum of the deviations from the mean is .......................................... than the sum of the deviations from median.
Answer:
more

True/False

State whether the following statements are true or false:

Question 1.
Mean of the squares of the deviations from mean is called the variance.
Answer:
True

Question 2.
The units of individual observations x_i and the unit of their mean x̄ are different from that of variance.
Answer:
True

Question 3.
The proper measure of dispersion about the mean of a set of observations is expressed as positive square root of the variance.
Answer:
True

Question 4.
The series having smaller coefficient of variation is said to be more variable than the other.
Answer:
False

Question 5.
The series with greater standard deviation is called more variable.
Answer:
True

Question 6.
Adding or subtracting a positive number to or from each observation of a group affect the variance.
Answer:
False

Question 7.
Statistics is as old as human civilisation.
Answer:
True

Question 8.
Sir Ronald A. Fisher is known as the father of modern statistics.
Answer:
True
Question 9.
Mean and mode are the only two measures of central of tendency.
Answer:
False

Question 10.
Measures of central tendency are sufficient to give complete information about a given data.
Answer:
False