RBSE Class 11 Maths Important Questions Chapter 13 Limits and Derivatives

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 13 Limits and Derivatives Questions and Answers.

RBSE Class 11 Maths Chapter 13 Important Questions Limits and Derivatives

Question 1.
If y = 1 + \(\frac{x}{1 !}+\frac{x^2}{2 !}+\frac{x^3}{3 !}\) + ....................... then prove that \(\frac{d y}{d x}\) = y.
Answer:

Question 2.
Find the derivative of the function e^x log √x tan x.
Answer:

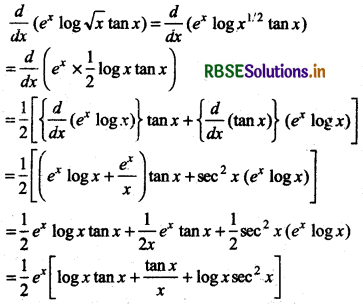
Question 3.
Find the derivative of function \(\frac{\cos x-x \sin x}{x \cos x+\sin x}\).
Answer:

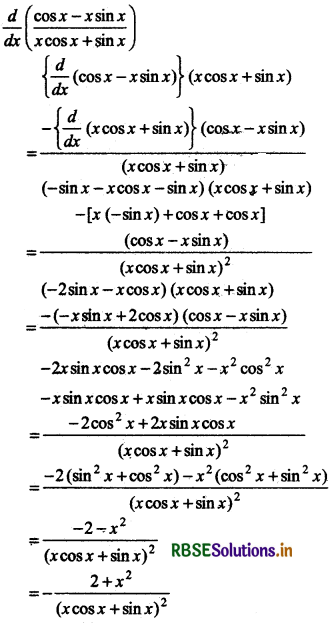
Question 4.
If y = \(\sqrt{\frac{1-x}{1+x}}\) then prove that (1 - x²) \(\frac{d y}{d x}\) + y = 0.
Answer:

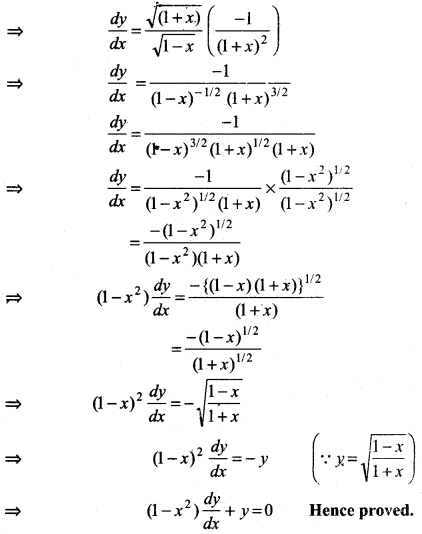
Question 5.
Evaluate the following:
(i) \(\lim _{x \rightarrow 0}\left(\frac{5^{3 x}-4^{2 x}}{x}\right)\)
Answer:

(ii) \(\lim _{x \rightarrow 0}\left(\frac{7^{2 x}-1}{5^{3 x}-1}\right)\)
Answer:

Question 6.
Evaluate:
\(\lim _{y \rightarrow 1} \frac{y^2-\sqrt{y}}{\sqrt{y}-1}\)
Answer:

Question 7.
Evaluate:
\(\lim _{x \rightarrow 5} \frac{5-\sqrt{20+x}}{3-\sqrt{14-x}}\)
Answer:

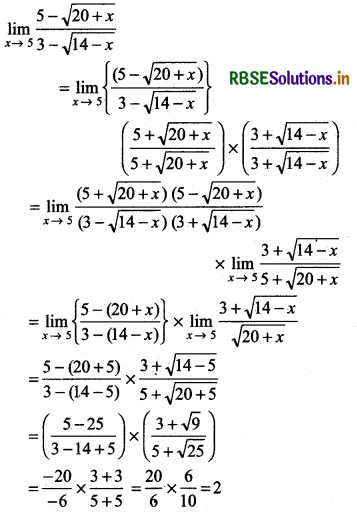
Question 8.
Evaluate:
\(\lim _{x \rightarrow 0} \frac{\left(\sqrt{1+x+x^2}-\sqrt{x+1}\right)}{2 x^2}\)
Answer:

Question 9.
Evaluate:
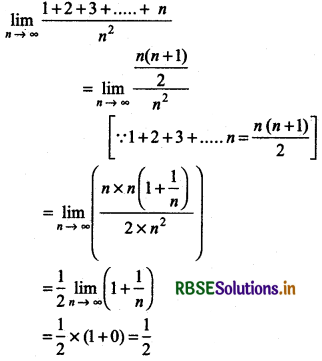
\(\lim _{n \rightarrow \infty} \frac{1+2+3+\ldots \ldots+n}{n^2}\)
Answer:

Question 10.
Evaluate:
\(\lim _{n \rightarrow \infty} \frac{1^2+2^2+3^2+\ldots \ldots+n^2}{n^3}\)
Answer:

Question 11.
Evaluate:
\(\lim _{n \rightarrow \infty} \frac{1^3+2^3+3^3+\ldots \ldots+n^3}{n^4}\)
Answer:

Question 12.
Evaluate:
\(\lim _{x \rightarrow 0} \frac{\cos 4 x-\cos 8 x}{\cos 5 x-\cos 7 x}\)
Answer:

Question 13.
Evaluate:
\(\lim _{x \rightarrow 0} \frac{3 \sin x-\sin 3 x}{x^3}\)
Answer:

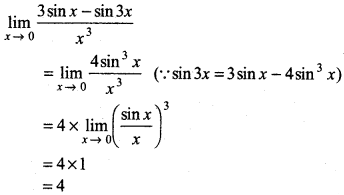
Multiple choice Questions

Question 1.
\(\lim _{x \rightarrow 3} \frac{\left[x^3-5 x^2+6 x\right]}{\left(x^2-9\right)}\) equals:
(a) \(\frac{1}{2}\)
(b) 2
(c) 1
(d) None of these
Answer:
(a) \(\frac{1}{2}\)

Question 2.
\(\lim _{x \rightarrow 0} \frac{(x+1)^5-1}{x}\) equals:
(a) 5
(b) \(\frac{1}{5}\)
(c) \(\frac{2}{5}\)
(d) None of these
Answer:
(a) 5

Question 3.
\(\lim _{z \rightarrow 0} \frac{z^{1 / 3}-1}{z^{1 / 6}-1}\) equals:
(a) 2
(b) 1
(c) - 2
(d) None of these
Answer:
(a) 2

Question 4.
\(\lim _{x \rightarrow 0}\) f(x) equals, where

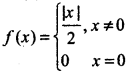
(a) Not exist
(b) 1
(c) - 1
(d) None of these
Answer:
(b) 1

Question 5.
\(\lim _{x \rightarrow 0}\) f(x) equals, where

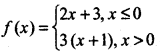
(a) 3
(b) - 3
(c) 2
(d) None of these
Answer:
(a) 3

Question 6.
\(\lim _{x \rightarrow 1}\) f(x) equals, where

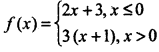
(a) 6
(b) 1
(c) - 1
(d) None of these
Answer:
(a) 6

Question 7.
\(\lim _{x \rightarrow 5}\) f(x) where f(x) = |x| - 5:
(a) 0
(b) 1
(c) - 1
(d) None of these
Answer:
(a) 0

Question 8.
If

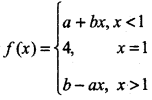
and \(\lim _{x \rightarrow 1}\) f(x) = f(1) then, value of a and b are:
(a) a = 0, b = 4
(b) a = 4, b = 0
(c) a = - 4, b = 1
(d) None of these
Answer:
(a) a = 0, b = 4

Question 9.
If

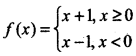
then \(\lim _{x \rightarrow 0}\) equals:
(a) Not exists
(b) 1
(c) 0
(d) None of these
Answer:
(a) Not exists

Question 10.
If

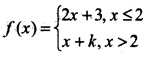
and \(\lim _{x \rightarrow 2}\) f(x) exists then value of k is:
(a) 5
(b) 3
(c) 4
(d) None of these
Answer:
(a) 5

Question 11.
\(\lim _{x \rightarrow 5^5}\) f(x) equals, where

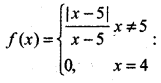
(a) - 1
(b) 1
(c) 0
(d) None of these
Answer:
(a) - 1

Question 12.
\(\lim _{n \rightarrow \infty} \frac{1^2+2^2+3^2+\ldots+n^2}{n^2}\) equals:
(a) \(\frac{1}{3}\)
(b) 1
(c) \(\frac{1}{2}\)
(d) None of these
Answer:
(a) \(\frac{1}{3}\)

Question 13.
\(\lim _{n \rightarrow \infty} \frac{1^3+2^3+3^3+\ldots .+n^3}{n^4}\) equals:
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{2}\)
(d) None of these
Answer:
(a) \(\frac{1}{4}\)

Question 14.
\(\lim _{x \rightarrow 0} \frac{2^x-1}{(1+x)^{1 / 2}-1}\) equals:
(a) 2 log 2
(b) log 2
(c) 2
(d) None of these
Answer:
(a) 2 log 2

Question 15.
\(\lim _{x \rightarrow 1} \frac{x-1}{2 x^2-7 x+5}\) equals:
(a) \(\frac{1}{3}\)
(b) - \(\frac{1}{3}\)
(c) 3
(d) None of these
Answer:
(b) - \(\frac{1}{3}\)

Question 16.
\(\lim _{x \rightarrow \infty}\left(\frac{x+2}{x+1}\right)^{x+3}\) equals:
(a) \(\frac{1}{e}\)
(b) e
(c) e²
(d) None of these
Answer:
(b) e

Question 17.
\(\lim _{x \rightarrow 0} \frac{a x e^x-b \log (1+x)+c x e^{-x}}{x^2 \sin x}\) equals:
(a) 1
(b) 2
(c) - 1
(d) None of these
Answer:
(b) 2

Question 18.
\(\lim _{x \rightarrow 0} \frac{a x e^x-b \log (1+x)+c x e^{-x}}{x^2 \sin x}\) equals:
(a) - 1
(b) 2
(c) 1
(d) None of these
Answer:
(b) 2

Question 19.
\(\lim _{x \rightarrow 0} \frac{\pi / 2}{\cot \left(\frac{\pi}{2} x\right)}\) equals:
(a) π/2
(b) π²/2
(c) π/4
(d) None of these
Answer:
(b) π²/2

Question 20.
\(\lim _{x \rightarrow \pi / 2}\) tan² x [(2 sin^2x + 3 sin x + 4)^1/2 - (sin² x + 6 sin x + 2)] equals:
(a) 12
(b) \(\frac{1}{12}\)
(c) 1
(d) None of these
Answer:
(b) \(\frac{1}{12}\)

Fill in the Blanks

Question 1.
Velocity is the rate of change of ..................................
Answer:
displacement

Question 2.
If the right and left hand limits coincide, we call that common value as the .................................
Answer:
limit

Question 3.
If f (x) = 3x, then at x = 2, the derivative is .................................. .
Answer:
3

Question 4.
The derivative of sin x at x = 0 is .................................. .
Answer:
1

Question 5.
..................................... is the derivative of sin² x.
Answer:
sin 2x

True/False

State whether the following statements are true or false:

Question 1.
If x → a, f(x) → 1, then limit of function f(x) is denoted as \(\lim _{x \rightarrow a}\) f (x) = 1.
Answer:
True

Question 2.
\(\lim _{x \rightarrow a}\) f (x) is the right hand limit of f at a.
Answer:
False

Question 3.
\(\lim _{x \rightarrow a}\) f (x) is the left hand limit of f at a.
Answer:
False

Question 4.
The limit of \(\lim _{x \rightarrow 1}\) (x³ - x² + 1) is 1.
Answer:
True

Question 5.
The derivative of f (x) = a for a fixed real value a is 0.
Answer:
True