RBSE Class 11 Maths Important Questions Chapter 12 त्रिविमीय ज्यामिति का परिचय

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 12 त्रिविमीय ज्यामिति का परिचय Important Questions and Answers.

RBSE Class 11 Maths Chapter 12 Important Questions त्रिविमीय ज्यामिति का परिचय

अतिलघूत्तरात्मक प्रश्न-

प्रश्न 1.
ज्ञात कीजिए कि निम्न बिन्दु किस अष्टांश (Octants) में स्थित हैं -
(i) (3, 1, 2)
(ii) (3, 1, 2)
हल:
(i) चूँकि बिन्दु A का x-निर्देशांक धन, y-निर्देशांक ऋण और निर्देशांक धन है। अत: बिन्दु A अष्टांश OXYZ में स्थित होगा।
(ii) बिन्दु Bax, y- तथा z - निर्देशांक धन हैं । अत: बिन्दु B अष्टांश OXYZ में स्थित होगा।

प्रश्न 2.
बिन्दु (x, y, z) की तीन निर्देशांक तलों से लाम्बिक दूरियाँ लिखिए ।
हल:
माना बिन्दु P = (x, y, z ) बिन्दु P की XY तल से दूरी = |z|, बिन्दु P की YZ तल से दूरी = |x|, बिन्दु P की ZX तल से दूरी = |y|

प्रश्न 3.
रिक्त स्थानों की पूर्ति कीजिए-
(i) x-अक्ष तथा 1-अक्ष संयुक्त रूप से एक तल बनाते हैं उस तल को ............................ तल कहते हैं।
हल:
XY तल

(ii) XY-तल में स्थित बिन्दु के निर्देशांक का रूप ................................. तल होता है।
हल:
(x, y, 0)

(iii) निर्देशांक तल अन्तरिक्ष को ................................ अष्टांशों में विभाजित करते हैं|
हल:
8

प्रश्न 4.
बिन्दुओं (1, 2, 3) तथा ( 3, - 4 - 5) से होकर निर्देशांक तलों के समानान्तर तल खींचे गये हैं । इस प्रकार बने समानान्तर षड्फलकी की कोरों की माप ज्ञात कीजिए।
हल:
(|x₂ - x₁|, |y₂ - y₁|, |z₂ - z₁|)

प्रश्न 5.
बिन्दु P (α, β, γ) की निर्देशांक्षों से दूरियाँ ज्ञात कीजिए ।
हल:
x - अक्ष से दूरी = \(\sqrt{\beta^2+\gamma^2}\)
y - अक्ष से दूरी = \(\sqrt{\alpha^2+\gamma}\)
z - अक्ष से दूरी = \(\sqrt{\alpha^2+\beta^2}\)

प्रश्न 6.
बिन्दु (1, 2, 3) की निर्देश अक्षों से दूरी लिखिए।
हल:

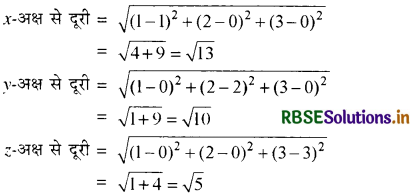
प्रश्न 7.
एक त्रिभुज जिसके शीर्ष के निर्देशांक (x₁, y₁, z₁), (x₂, y₂, z₂) और (x₃, y₃, z₃) हैं, के केन्द्रक के निर्देशांक हैं ।
हल:
\(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)

प्रश्न 8.
चतुष्फलक का केन्द्रक लिखिए।
हल:
\(\left(\frac{x_1+x_2+x_3+x_4}{4}, \frac{y_1+y_2+y_3+y_4}{4}, \frac{z_1+z_2+z_3+z_4}{4}\right)\)

प्रश्न 9.
बिन्दुओं (1, 3, 4) और (4, 6. 2) को मिलाने से बने रेखाखण्ड को 1 : 2 में अन्त: विभाजित करने वाले बिन्दु के निर्देशांक ज्ञात कीजिए।
हल:

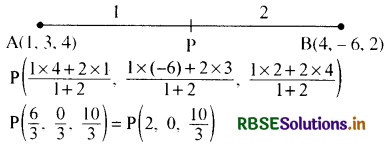
प्रश्न 10.
x का मान ज्ञात कीजिए यदि बिन्दुओं P (x - 8, 4) तथा Q (- 3, - 5, 4) के बीच की दूरी 5 है ।
हल:
दिया गया बिन्दु P = (x, - 8, 4) तथा Q = (- 3, - 5, 4)
∴ (PQ)² = (x + 3)² + (- 8 + 5)² + (4 - 4)² प्रश्नानुसार, PQ = 5
∴ PQ² = 25
अतः ⇒ (x + 3)² + (- 3)² + 0 = 25
⇒ (x + 3)² = 25 - 9 = 16
⇒ (x + 3) = ± 4
∴ x = 1, -

लघूत्तरात्मक प्रश्न

प्रश्न 1.
सिद्ध कीजिए कि निम्न तीन बिन्दु सरेख हैं-
(i) (4, - 3, - 1), (5, - 7, 6), (3, 1, - 8)
(ii) (0, 7, - 7), (1, 4, - 5), (- 1, 10, - 9)
हल:
(i) माना कि दिए गए तीन बिन्दु क्रमश: A (4, - 3, - 1), B (5 - 7, 6) तथा C (3, 1, - 8 ) हैं।

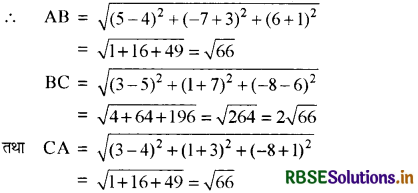
∵ AB + AC ∴ दिए गए बिन्दु सरेख हैं।

(ii) (0, 7, - 7), (1, 4, - 5), (- 1, 10, - 9). माना ये तीन बिन्दु A, B व C हैं।

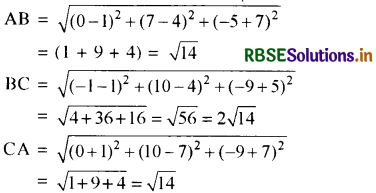
∵ BC = AB + AC ∴ दिए गए बिन्दु सरेख हैं।

प्रश्न 2.
बिन्दुओं O (0, 0, 0), A (a, 0, 0), B (0, b, 0), C (0, 0, c) से समान दूरी पर स्थित बिन्दु के निर्देशांक ज्ञात कीजिए।
हल:
माना P (x, y, z) अभीष्ट बिन्दु है।
अतः प्रश्नानुसार OP = PA = PB = PC
∴ OP² = PA²
⇒ x² + y² + z² = (x - a)² + (y - 0)² + (z - 0)²
⇒ x = \(\frac{a}{2}\)
इसी प्रकार OP² = PB² से y = \(\frac{b}{2}\)
तथा OP² = PC² से y = \(\frac{c}{2}\)
∴ अभीष्ट बिन्दु के निर्देशांक \(\left(\frac{a}{2}, \frac{b}{2}, \frac{c}{2}\right)\) हैं।

प्रश्न 3.
प्रदर्शित कीजिए कि बिन्दु A (1, 2, 3), B = (- 1, - 2, - 1), C (2, 3, 2) तथा D ( 4, 7, 6) एक समान्तर चतुर्भुज के शीर्ष हैं।
हल:
कार्तीय विधि - दूरी सूत्र के उपयोग से

हम देखते हैं कि चतुर्भुज ABCD में
AB = CD = 67 BC = DA = √43 और AC ≠ BD
तब चतुर्भुज ABCD एक समान्तर चतुर्भुज होगा।
अत: दिये गये बिन्दु एक समान्तर चतुर्भुज के शीर्ष हैं।

प्रश्न 4.
YZ समतल में वह बिन्दु ज्ञात कीजिए जो बिन्दुओं A (a, 0, 0), B (0, b, 0), C (0, 0, c) से समान दूरी पर हो।
हल:
प्रश्नानुसार
A = (a, 0, 0)
B = (0, b, 0) तथा C = (0, 0, c)
माना YZ-समतल में वह बिन्दु P (0, y, z) है। तब
AP = \(\sqrt{a^2+y^2+z^2}\)
तथा BP = \(\sqrt{(b-y)^2+z^2}\)
CP = \(\sqrt{y^2+(c-z)^2}\)
∵ प्रश्नानुसार AP = BP = CP
⇒ AP² = BP² = CP²
∴ AP² = BP²
a² + y² + z² = (b - y)² + z²
⇒ a² + y² + z² = b² + y² - 2by + z²
⇒ 2by = b² - a²
⇒ y = \(\frac{b^2-a^2}{2 b}\)
पुन: AP² = CP² से
a² + y² + z² = y² + (c - z)²
⇒ a² + y² + z² = y² + c² + z² - 2cz
⇒ 2cz = c² - a²
∴ z = \(\frac{c^2-a^2}{2 c}\)
अत: अभीष्ट बिन्दु = (0, y, z)
= \(\left(0, \frac{b^2-a^2}{2 b}, \frac{c^2-a^2}{2 c}\right)\)

प्रश्न 5.
Z - अक्ष पर वह बिन्दु ज्ञात कीजिए जो बिन्दुओं A (1, 5, 7) तथा B (5, 1, - 4) से समान दूरी पर स्थित हो।
हल:
माना A (1, 5, 7) तथा B (5, 1, - 4) है तथा Z - अक्ष पर वह बिन्दु P (0, 0, z) है
∴ प्रश्नानुसार
AP = BP
AP² = BP²
⇒ (1 - 0)² + (5 - 0)² + (7 - z)² = (5 - 0)² + (1 - 0)² + (- 4 - z)²
⇒ 1 + 25 + 49 + z² - 14z = 25 + 1 + 16 + z² + 8z
⇒ 49 - 16 = 8z + 14z
⇒ 33 = 22z
⇒ z = \(\frac{33}{22}=\frac{3}{2}\)
अतः Z-अक्ष पर अभीष्ट बिन्दु (0, 0, z) = (0, 0, \(\frac{3}{2}\))

प्रश्न 6.
बिन्दु R रेखाखण्ड P (3, 4, 5), Q (2, 5, 4) को किस अनुपात में विभाजित करेगा यदि यह yz समतल पर हो। R के निर्देशांक भी ज्ञात कीजिए।
हल:
माना P (3, 4, 5) तथा Q (2, 5, 4) को मिलाने वाले रेखाखण्ड को yz समतल पर बिन्दु λ : 1 में विभाजित करता है तब R के निर्देशांक
= \(\left(\frac{3 \lambda+2}{\lambda+1}, \frac{4 \lambda+5}{\lambda+1}, \frac{5 \lambda+4}{\lambda+1}\right)\) ......... (1)
R के निर्देशांकों में x = 0 रखने पर क्योंकि yz समतल के लिए x = 0 होगा।

प्रश्न 7.
यदि P (3, 2, - 4), Q (5, 4, - 6) तथा R (9, 8, - 10) संरेख हैं तो ज्ञात कीजिए कि PR को Q किस अनुपात में बाँटेगा?
हल:
प्रश्नानुसार PQR सरेखीय हैं तथा Q, PR को λ : 1 में विभाजित
करता है तो Q के निर्देशांक \(\left(\frac{9 \lambda+3}{\lambda+1}, \frac{8 \lambda+2}{\lambda+1}, \frac{-10 \lambda-4}{\lambda+1}\right)\)
लेकिन Q के निर्देशांक (5, 4, - 6 ) हैं। अतः

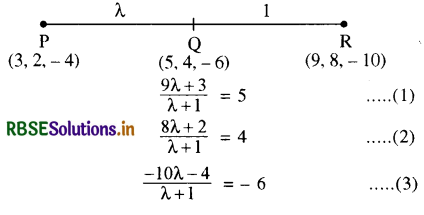
समीकरण (1), (2) व (3) में से (1) को हल करने पर
9λ + 3 = 5λ + 5
4λ = 2
λ = \(\frac{2}{4}\) = \(\frac{1}{2}\) ⇒ λ : 1 = 1 : 2
समीकरण (2) तथा (3) को भी हल करने पर λ का मान \(\frac{1}{2}\) ही प्राप्त होगा।
अत: Q, PR को 1 : 2 में विभाजित करता है।

प्रश्न 8.
उस बिन्दु का बिन्दुपथ ज्ञात कीजिए जिसकी बिन्दुओं A (3, 4, 5) तथा B (- 1, 3, - 7 ) से दूरियों के वर्गों का अन्तर 2λ² के बराबर हो ।
हल:
माना वह बिन्दु P (x, y, z ) है ।
अंत: PA² - PB² = 2λ²
[(x - 3)² + (y - 4)² + (z - 5)² - (x + 1)² - (y - 3)² - (z + 7)²] = 2λ²
या x² - 6x + 9 + y² - 8y + 16 + z² - 10z + 25 - x² - 2x - 1 - y² + 6y - 9 - z² - 14z - 49 = 2λ²
- 6x + 9 - 8y + 16 - 10z + 25 - 2x - 1 + 6y - 9 - 14z - 49 = 2λ²
या (- 6x - 2x) + (- 8y + 6y) + (- 10z - 14z) - 9 = 2λ²
या - 8x - 2y - 24z - 9 = 2λ²
या - 8x - 2y - 24z - 9 - 2λ² = 0
या 8x + 2y + 24z + 2λ² + 9 = 0
जो कि अभीष्ट बिन्दुपथ है।

प्रश्न 9.
वह अनुपात ज्ञात कीजिए जिसमें बिन्दुओं (- 2, 4, 7) तथा (3, - 5, 8) को मिलाने वाले रेखाखण्ड को समतल xy द्वारा विभाजित किया जाता है।
हल:
माना P (- 2, 4, 7) तथा Q (3, - 5, 8) को मिलाने वाले रेखाखण्ड xy को समतल बिन्दु R पर λ : 1 में विभाजित करता है। तब R के निर्देशांक
\(\left(\frac{3 \lambda-2}{\lambda+1}, \frac{-5 \lambda+4}{\lambda+1}, \frac{8 \lambda+7}{\lambda+1}\right)\)
∵ R समतल xy पर है अतः 2 के निर्देशांक = 0
⇒ \(\frac{8 \lambda+7}{\lambda+1}\) = 0 ⇒ 8λ + 7 = 0
या λ = - \(\frac{7}{8}\)
अतः अभीष्ट अनुपात 7 : 8 है। साथ ही λ < 0 अत: यह भी स्पष्ट है किxy तल रेखाखण्ड PQ को बाह्य विभाजित करता है।

प्रश्न 10.
त्रिभुज A, B, C के शीर्ष A (10, - 2, 8), B (8, 0, 7), C (10, 2, 8) हैं । त्रिभुज का परिमाप ज्ञात कीजिए ।
हल:
माना ABC एक त्रिभुज है तथा AB, BC तथा CA इसकी तीनों भुजाएँ हैं। अत:

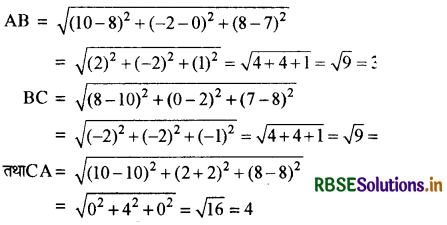
अतः ∆ ABC का परिमाप = AB + BC + CA
= 3 + 3 + 4 = 10

प्रश्न 11.
प्रदर्शित कीजिए कि बिन्दु A (0, 7, 10), B ( - 1, 6, 6) तथ C (- 4, 9, 6) समद्विबाहु समकोण त्रिभुज के शीर्ष हैं।
हल:
माना ABC एक समद्विबाहु समकोण त्रिभुज है। अतः
AB² = (- 1 - 0)² + (6 - 7)² + (6 - 10)²
= 1 + 1 + 16 = 18
BC² = (- 1 + 4)² + (6 - 9)² + (6 - 6)²
= 9 + 9 = 0 = 18
CA² = (0 + 4)² + (7 - 9)² + (10 - 6)²
= 16 + 4 + 16 = 36
∵ AB = BC तथा AB² + BC² = AC²
अत: A, B, C समद्विबाहु समकोण त्रिभुज के शीर्ष हैं।

प्रश्न 12.
एक त्रिभुज के केन्द्रक के निर्देशांक \(\left(\frac{4}{3}, \frac{4}{3}, \frac{1}{3}\right)\) तथा दो शीर्ष (1, 3, 4) एवं (5, - 2, 1) हैं, तीसरे शीर्ष के निर्देशांक ज्ञात कीजिए।
हल:
प्रश्नानुसार दिया गया है कि किसी त्रिभुज केन्द्रक के निर्देशांक \(\left(\frac{4}{3}, \frac{4}{3}, \frac{1}{3}\right)\), दो शीर्ष (1, 3, 4) व (5, - 2, 1) हैं तथा तीसरा शीर्ष हमें ज्ञात करना है।

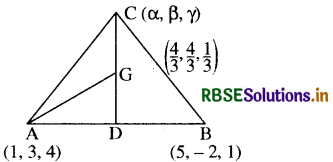
हम जानते हैं कि यदि किसी त्रिभुज के केन्द्रक के निर्देशांक (x, y, z) हों तथा उसके शीर्ष (x₁, y₁, z₁), (x₂, y₂, z₂) व (x₃, y₃, z₃) हों तो
(x, y, 2) = \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)
अतः दिए गए त्रिभुज ABC हेतु

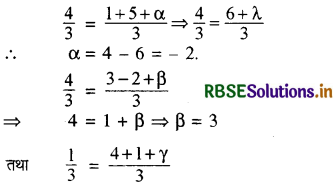
γ + 5 = 1
∴ γ = - 4
∴ तीसरे शीर्ष के निर्देशांक = ( - 2, 3, - 4)

प्रश्न 13.
एक बिन्दु जिसका ८ निर्देशांक 8 है तथा रेखाखण्ड P (2, -3, 4), Q (8, 0, 10) पर है। दूसरे निर्देशांक ज्ञात कीजिए।
हल:
यहाँ P (2, 3, 4) तथा Q (8, 0, 10) हैं। माना PQ पर कोई बिन्दु R है जिसके निर्देशांक (x, y, 8) हैं तथा माना कि R, PQ को λ : 1 में विभाजित करता है अतः R के निर्देशांक होंगे-

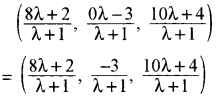
तथा R के निर्देशांक (x, y, 8) हैं।
अतः \(\frac{10 \lambda+4}{\lambda+1}\) = 8
⇒ 10λ + 4 = 8λ + 8
⇒ 10λ - 8λ = 8 - 4
⇒ 2λ = 4
∴ λ = 2
∴ x = \(\frac{8 \cdot 2+2}{2+1}=\frac{16+2}{3}=\frac{18}{3}\) = 6
तथा y = \(\frac{-3}{\lambda+1}=\frac{-3}{2+1}=\frac{-3}{3}\) = - 1
अत: R के निर्देशांक (6, - 1, 8)

निबन्धात्मक प्रश्न

प्रश्न 1.
A तथा B के निर्देशांक क्रमशः (- 2, 2, 3 ) तथा ( 13, - 3, 13 ) हैं। कोई बिन्दु P इस प्रकार गमन करता है कि 3PA = 2PB. सिद्ध करो कि P बिन्दु का बिन्दुपथ x² + y² + z² + 28x - 12y + 10z - 247 = 0 होगा।
हल:
माना कि बिन्दु P के निर्देशांक (x, y, z) हैं, तब
PA² = (x + 2)² (y - 2)² + (3 - 3)²
तथा PB² = (x - 13)² + (y + 3)² + (z - 13)²
अब दी हुई शर्त के अनुसार 3PA = 2PB
या 9A² = PB²
⇒ 9 {(x + 2)² + (x - 2)² + (z - 3)²} = 4{(x - 13)² + (y + 3)² + (z - 13)²}
⇒ 9 [x² + 4x + 4 + y² - 4y + 4 + z² - 6z + 9] = 4[x² - 26x + 169 + y² + 6y + 9 + z² - 26z + 169]
⇒ 9x² + 36x + 36 + 9y² - 36y + 36 + 9z² - 54z + 81
= 4x² - 104x + 676 + 4y² + 24y + 36 + 4z² - 104z + 676
⇒ 9x² + 9y² + 9z² + 36x - 36y - 54z + 153
= 4x² + 4y² + 4z² - 104x + 24y - 104z + 1388
⇒ 9x² - 4x² + 9y² - 4y² + 9z² - 4z² + 140x 60y + 50z - 1235 = 0
⇒ 5x² + 5y² + 5z² + 140x - 60y + 50z - 1235 = 0
⇒ x² + y² + z² + 28x - 12y + 10z - 247 = 0
जो कि बिन्दु P का अभीष्ट बिन्दुपथ है।

प्रश्न 2.
यदि बिन्दु A (3, 2, 0), B (5, 3, 2) तथा C (- 9, 6, - 3) एक त्रिभुज का निर्माण करते हैं। रेखा AD कोण BAC को समद्विभाजित करती है तथा BC को D पर काटती है। बिन्दु D के निर्देशांक ज्ञात कीजिए ।
हल:
हम जानते हैं कि किसी भी त्रिभुज में शीर्ष कोण की अन्तः समद्विभाजक रेखा सामने की भुजा को शेष दो भुजाओं के अनुपात में विभाजित करती है।

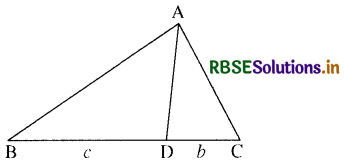
∴ c² = AB² = (5 - 3)² + (- 3 - 2)² + (2 - 0)²
= 2² + 1² + 2² = 9.
⇒ C = √9 = 3
b² = AC² = (- 9 - 3)² + (6 - 2)² + (3 - 0)²
= 12² + 4² + 3²
= 144 + 16 + 9 = 169
⇒ b = √169 = 13
या b = 13
अतः λ = \(\frac{3}{13}\)

(i) यदि AD कोण BAC को अंत: विभाजित करता है तब λ = \(\frac{3}{13}\)
अत: D के निर्देशांक

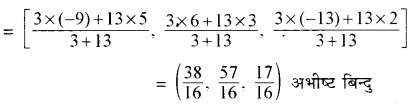
(ii) यदि AD कोण BAC को बाह्य विभाजित करता है, तब λ = \(\frac{3}{-13}\) इस स्थिति में बिन्दु D के निर्देशांक

बहुचयनात्मक प्रश्न

प्रश्न 1.
बिन्दु (x, y, z) की z-अक्ष से लम्बवत् दूरी है-
(A) \(\frac{z}{\sqrt{x^2+y^2+z^2}}\)
(B) \(\sqrt{x^2+y^2}\)
(C) 1
(D) z
हल:
(B) \(\sqrt{x^2+y^2}\)

प्रश्न 2.
बिन्दु (1, 2, 3) की x-अक्ष से दूरी है-
(A) √5
(B) √10
(C) √13
(D) 1
हल:
(C) √13

प्रश्न 3.
त्रिभुज जिसके शीर्ष (x₁, y₁, z₁), (x₂, y₂, z₂) तथा (x₃, y₃, z₃) हों, के केन्द्रक के निर्देशांक हैं-

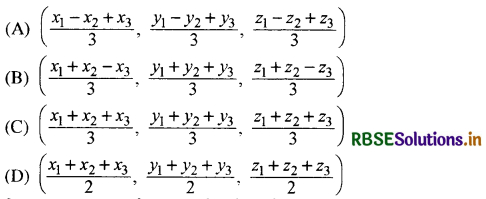
हल:
(C) \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)

प्रश्न 4.
बिन्दु P (a, b, c) की Z-अक्ष से दूरी होगी -
(A) \(\sqrt{\left(b^2+c^2\right)}\)
(B) \(\sqrt{\left(a^2+c^2\right)}\)
(C) \(\sqrt{\left(a^2+b^2\right)}\)
(D) \(\sqrt{\left(a^2+b^2+c^2\right)}\)
हल:
(C) \(\sqrt{\left(a^2+b^2\right)}\)

प्रश्न 5.
एक चर बिन्दु इस प्रकार गति करता है कि x = a तथा y = b तो इसका बिन्दुपथ होगा-
(A) XY - समतल के समान्तर एक समतल
(B) X- अक्ष के समान्तर एक रेखा
(C) Y-अक्ष के समान्तर एक रेखा
(D) Z-अक्ष के समान्तर एक रेखा
हल:
(D) Z-अक्ष के समान्तर एक रेखा

प्रश्न 6.
यदि P (1, - 2, 3), Q (2, 3, - 4) तथा R (0, - 7, 10) सरेखीय हों तो Q, PR को विभाजित करता है-
(A) 1 : 2 बाह्य
(C) 3 : 2 बाह्य
(B) 1 : 2 आन्तरिक
(D) 3 : 2 आन्तरिक
हल:
(A) 1 : 2 बाह्य

प्रश्न 7.
बिन्दुओं (2, 4, 8) तथा (3, 5, - 7) का मध्य बिन्दु है-
(A) (2, 4, 8)
(B) (3, 5, 1/2)
(C) \(\left(\frac{5}{2}, \frac{9}{2}, \frac{1}{2}\right)\)
(D) (3, 5, 0)
हल:
(C) \(\left(\frac{5}{2}, \frac{9}{2}, \frac{1}{2}\right)\)

प्रश्न 8.
बिन्दुओं (a₁, b₁, c₁), (a₂, b₂, c₂) को मिलाने वाली रेखाखण्ड को xy समतल किस अनुपात में विभाजित करेगा-
(A) C₁ : C₂
(B) a₁ : a₂
(C) C₂ : C₁
(D) C₂ : C₂
हल:
(A) C₁ : C₂

प्रश्न 9.
बिन्दु (0, 0, -4) का xy तल में प्रतिबिम्ब है.
(A) (0, 0, 0)
(B) (0, 0, 4)
(C) (0, 0, ± 4 )
(D) इनमें से कोई नहीं
हल:
(B) (0, 0, 4)

प्रश्न 10.
चतुष्फलक (x_i, y_i, z_i) i = 1, 2, 3, 4 के केन्द्रक के निर्देशांक हैं-

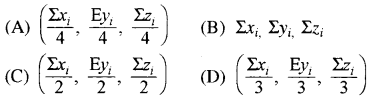
हल:
(A) \(\left(\frac{\Sigma x_i}{4}, \frac{E y_i}{4}, \frac{\Sigma z_i}{4}\right)\)

प्रश्न 11.
उस बिन्दु के निर्देशांक जो बिन्दुओं (0, 0, 0), (a, 0, 0), (0, b, 0) तथा (0, 0, c) से समान दूरी पर हैं, होंगे-

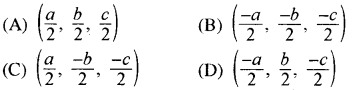
हल:
(A) \(\left(\frac{a}{2}, \frac{b}{2}, \frac{c}{2}\right)\)

प्रश्न 12.
एक ऐसा बिन्दु जो yz - तल में स्थित हो, के निर्देशांक होते हैं-
(A) (x, 0, z)
(B) (0, y, z)
(C) (0, 0, z)
(D) (x, y, 0)
हल:
(B) (0, y, z)

प्रश्न 13.
बिन्दु (5, 3, 2), (3, 2, 5) तथा ( 2, 5, 3) किस तरह के त्रिभुज के शीर्ष हैं?
(A) समद्विबाहु त्रिभुज के
(B) समबाहु त्रिभुज के
(C) समकोण त्रिभुज के
(D) इनमें से कोई नहीं
हल:
(B) समबाहु त्रिभुज के

रिक्त स्थानों की पूर्ति करो

प्रश्न 1.
त्रिविमीय ज्यामिति के समकोणिक कार्तीय निर्देशांक निकाय में निर्देशांक्ष तीन परस्पर ............................... रेखाएँ होती हैं।
हल:
लम्बवत

प्रश्न 2.
तीन निर्देशांक्ष तल अन्तरिक्ष को आठ भागों में बाँटतें हैं जिन्हें ...................................... कहते हैं।
हल:
अष्टांश

प्रश्न 3.
............................................ पर किसी बिन्दु के निर्देशांक (x, 0, 0) हैं
हल:
x - अक्ष

प्रश्न 4.
दो बिन्दुओं P(x₁, y₁, z₁ ) व Q(x₂, y₂, z₂) के मध्य बिन्दु के निर्देशांक .......................... हैं।
हल:
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\)

प्रश्न 5.
एक त्रिभुज जिसके शीर्षों के निर्देशांक (x₁, y₁, z₁), (x₂, y₂, z₂) और (x₃, y₃, z₃) हैं, के केन्द्रक के निर्देशांक हैं :
हल:
\(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)

प्रश्न 6.
बिन्दु P (-2, 4, 1) और Q(1, 2, - 5) के बीच की दूरी ..................................... है।
हल:
7 इकाई

प्रश्न 7.
बिन्दु A( 4, - 3, - 1), B(5, - 7, 6) और C (3, 1, - 8) ................................. हैं।
हल:
संरेखीय

प्रश्न 8.
बिन्दु P (2, 3, 5) की XY - समतल से दूरी .......................................... हैं।
हल:
5 इकाई

प्रश्न 9.
बिन्दु P (3, 4, 5) की z-अक्ष से दूरी ....................................... है।
हल:
5 इकाई

प्रश्न 10.
y-अक्ष पर बिन्दु के निर्देशांक, जो बिन्दु ( 1, 2, 3 ) से √10 इकाई दूरी पर हैं, ..................................... होंगे।
हल:
(0, 2, 0)

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए

प्रश्न 1.
बिन्दु P(a, b, c ) की 2- अक्ष से लम्बवत् दूरी \(\sqrt{a^2+b^2}\) होती है।
हल:
सत्य

प्रश्न 2.
बिन्दु P(3, 3, 4) की r- अक्ष से दूरी 3 इकाई है।
हल:
असत्य

प्रश्न 3.
बिन्दु P( 6, 7, 8) की xy - समतल से लम्बवत् दूरी 8 इकाई है।
हल:
सत्य

प्रश्न 4.
उस बिन्दु का बिन्दुपथ जिसके लिए y = 0, z = 0, x-अक्ष होता है।
हल:
सत्य

प्रश्न 5.
XOZ – समतल बिन्दुओं (2, 3, 1) और (6, 7, 1) को 2:7 में विभाजित करता है।
हल:
असत्य

प्रश्न 6.
यदि तीन बिन्दु A (3, 2, - 4), B (9, 8, - 10 ) और C (5, 4, 6) संरेखीय हैं तब बिन्दु C, AB को 2 : 3 में विभाजित करता है।
हल:
असत्य

प्रश्न 7.
त्रिभुज ABC के शीर्षों के निर्देशांक A(x₁, y₁, z₁), B(x₂, y₂, z₂), C(x₃, y₃, z₃) हो तो केन्द्रक के निर्देशांक होते हैं।
हल:
सत्य

प्रश्न 8.
त्रिभुज ABC में शीर्षों A( 0, 0, 6), B (0, 4, 0) और C (6, 0, 0) की उस माध्यिका की लम्बाई जो B से गुजरती है, √34 है।
हल:
सत्य

प्रश्न 9.
बिन्दुओं P (- 2, 3, 1) तथा Q (2, 1, 2) के मध्य दूरी 21 इकाई है।
हल:
असत्य

प्रश्न 10.
बिन्दु (a, b, c), (b, c, a) और (c, a, b) समबाहु त्रिभुज के शीर्षों के निर्देशांक हैं।
हल:
सत्य

सही मिलान कीजिए

भाग (A)	भांग (B)
1. बिन्दुओं P ( 1, 2, 3) व Q (-1, -1, -1 ) के मध्य दूरी	(a) x - 2y - z + 1 = 0
2. बिन्दुओं A ( 0, 2, 3) व (2, −2, 1) से समान दूरी पर रहने वाले बिन्दु का बिन्दुपथ	(b\(\left(\frac{14}{5}, \frac{3}{5}, \frac{16}{5}\right)\)
3. y - अक्ष पर स्थित वह बिन्दु जो बिन्दुओं (3, 1, 2) व (5, 5, 2) से बराबर दूरी पर हो	(c) – 3 : 7
4. z-अक्ष पर स्थित वह बिन्दु जो बिन्दु (1, 2, 3) से √21 दूरी पर हो	(d) (1, 2, - 2)
5. बिन्दुओं P(2 - 1, 4) व Q( 4, 3, 2) को मिलाने वाली रेखा को 2 : 3 में अन्तःविभाजित करने वाले बिन्दु के निर्देशांक	(e) 3 : 2
6. A ( 0, 0,6), B(0, 4, 0) व C(6, 0, 0) त्रिभुज के शीर्ष हैं तो C से जाने वाली माध्यिका की लम्बाई	(f) √29
7. शीर्षों ( 1, 2, −3), (3, 0, 1 ) व (-1, 1, - 4) वाले त्रिभुज के केन्द्रक के निर्देशांक	(g) 1 : 2
8. अनुपात, जिसमें Q (5, 4, -6), PR को अन्तःविभाजित करता है जहाँ P(3, 2, - 4 ) व R ( 9, 8 - 10 ) हैं।	(h) (0, 0, 7)
9. अनुपात, जिसमें C (7, 0, – 1), AB को बाह्य विभाजित करता है, जहाँ A (- 2, 3, 5) और B ( 1, 2, 3 ) हैं।	(i) (0, 5, 0)
10. बिन्दुओं ( 2, 3, 1) और ( 6, 7, 1) को मिलाने वाली रेखा को XOZ- समतल जिस अनुपात में विभाजित करता है।	(j) 7

हल:
1. (f)
2. (a)
3. (i)
4. (h)
5. (b)
6. (j)
7. (d)
8. (g)
9. (e)
10. (c)