RBSE Class 11 Maths Important Questions Chapter 12 Introduction to three Dimensional Geometry

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 12 Introduction to three Dimensional Geometry Questions and Answers.

RBSE Class 11 Maths Chapter 12 Important Questions Introduction to three Dimensional Geometry

Question 1.
Show that point (- 2, - 1, 6), (4, 0, 6),(3, 3,6) and (- 3, 2, 6) are vertices of a parallelogram but it is not a rectangle.
Answer:
Let
A(x₁, y₁, z₁) = A(- 2, - 1, 6)
B(x₂, y₂, z₂) = B(4, 0, 6)
C(x₃, y₃, z₃) = C(3, 3, 6)
D(x₄, y₄, z₄) = D(4, 0, 6)

Opposite sides
AB = CD = √37
BC = DA = √10
Thus, given points are vertices of a parallelogram

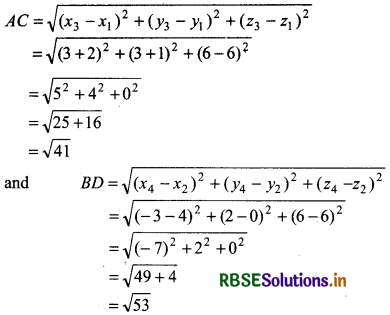
We see that diagonal AC ≠ diagonal BD
√41 ≠ √53
Thus, quadrilateral is a parallelogram but not a rectangle.
Hence proved.

Question 2.
Find the equation of the set of those points which are equidistant from the point 4(4, 5, - 6) and B(-4, 2, 7).
Answer:
Let point P(x, y, z) is such that
PA = PB
Then PA = \(\sqrt{(x-4)^2+(y-5)^2+(z+6)^2}\)
and PB = \(\sqrt{(x+4)^2(y-2)^2+(z-7)^2}\)
Given, PA = PB
Then \(\sqrt{(x-4)^2+(y-5)^2+(z+6)^2}\)
= \(\sqrt{(x+4)^2+(y-2)^2+(z-7)^2}\)
Squaring both sides, we have
(x - 4)² + (y - 5)² + (z + 6)² = (x + 4)² + (y - 2)² + (z - 7)²
⇒ x² - 8x + 16 + y² - 10y + 25 + z² + 12z + 36 = x² + 8x + 16 + y² - 4y + 4 + z² - 14z + 49
⇒ - 8x - 8x - 10y + 4y + 12z + 14z = 49 - 36 - 25 + 4
⇒ - 16x - 6y + 26z = - 8
⇒ 8x + 3y - 13z = 4
Thus, the required equation is
8x + 3y - 13z = 4

Question 3.
The centroid of a triangle PQR is (2, 3, 4). If coordinates of P and Q are respectively (7, - 4, 0) and (5, 2, 8), then find the coordinates of vertex R.
Answer:
Let coordinates of point R be (x, y, z),
Coordinates of centroid G = (2,3, 4)
Then coordinates of centroid

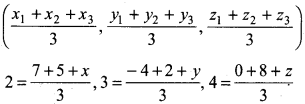
⇒ 2 × 3 = 12 + x, 3 × 3 = - 2 + y, 3 × 4 = 8 + z
⇒ 6 - 12 = x, 9 + 2 = y, 12 - 8 = z
x = - 6, y = 11, z = 4
Thus, coordinates of vertex R (x₁, y₁, z₁) = (- 6, 11, 4)

Question 4.
Show that point(4, 7, 8), (2, 3, 4), (- 1, - 2, 1) and (1, 2, 5) are vertices of a parallelogram.
Answer:
Let A(4, 7, 8), B(2, 3, 4), C(- 1, - 2, 1) and D(1, 2, 5) given point.

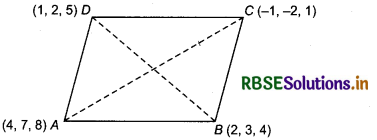
If A, B, C and D are vertices of a parallelogram, then AB = CD and BC = DA
i.e. opposite sides of a quadrilateral will be equal and AC ≠ BD diagonals will not be equal.

So, AB = CD, BC = DA
But diagonal AC ≠ diagonal BD
Thus, given points are vertices of a parallelogram.

Question 5.
Show that points (5, - 1, 1), (7, - 4, 7), (1, - 6, 10) and (- 1, - 3, 4) are vertices of a rhombus.
Answer:
Let A(5, - 1, 1), B(7, - 4, 7), C(1, - 6, 10) and D(- 1, - 3, 4) are given points.

∴ AB = BC = CD = DA
But diagonal AC ≠ diagonal BD
Thus, given points are vertices of a rhombus.

Question 6.
Coordinates of mid-points of sides of a triangle are(1, 5, - 1), (0, 4, - 2) and (2, 3, 4), then find the coordinates of its vertices.
Answer:
Let A(x₁, y₁, z₁), B(x₂, y₂, z₂) and C(x₃, y₃, z₃) are vertices of triangle and D(1, 5, - 1), E (0, 4, - 2) and F(2, 3, 4) are mid-points of sides BC, CA and AB respectively, then

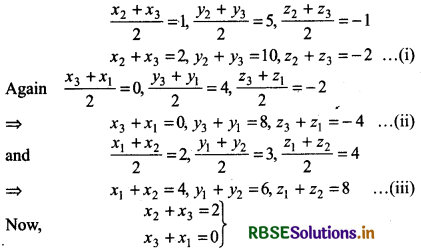
x₁ + x₂ = 4 on adding
2(x₁ + x₂ + x₃) = 6
⇒ x₁ + x₂ + x₃ = 3
Similarly by y₂ + y₃ = 10, y₃ + y₁ = 8, y₁ + y₂ = 6
2(y₁ + y₂ + y₃) = 24
⇒ y₁ + y₂ + y₃ = 12
and z₂ + z₃ = - 2, z₃ + z₁ = - 4, z₁ + z₂ = 8
2(z₁ + z₂ + z₃) = 2
z₁ + z₂ + z₃ = 1
Solving the equation
x₂ + x₃ = 2, x₃ + x₁ = 0, x₁ + x₂ =4
and x₁ + x₂ + x₃ = 3
x₁ = 1, x₂ = 3, x₃ = - 1
Again solving the equations
y₂ + y₃ = 10, y₃ + y₁ = 8, y₁ + y₂ = 6
and y₂ + y₂ + y₃ = 12
y₁ = 2, y₂ = 4, y₃ = 6
and solving the equations z₂ + z₃ = - 2, z₃ + z₁ = - 4 and z₁ + z₂ = 8 and z₁ + z₂ + z₃ = 1
z₁ = 3, z₂ = 5, z₃ = - 7
∴ Vertices of ABC are A(1, 2, 3), B(3, 4, 5) and C(- 1, 6, - 7)

Question 7.
If points A(3, 2, 0), B(5, 3, 2), C(- 9, 6, - 3) formed a triangle ABC and bisector of angle ∠ABC i.e., AD meet side BC at point D, then find coordinates of point D.
Answer:
AD is bisector of ∠BAC.

Question 8.
Find the ratio in which (3, - 1, 2) and (9, - 3, 6) lines joining the points is divided by curve x² + y² + z² = 350.
Answer:
Let line joining the points (3, - 1, 2) and (9, - 3, 6) meet the curve x² + y² + z² = 350 at point (x₁, y₁, z₁) and divides in the ratio.
λ : 1
∴ x₁² + y₁² + z₁² = 350 ..................... (i)

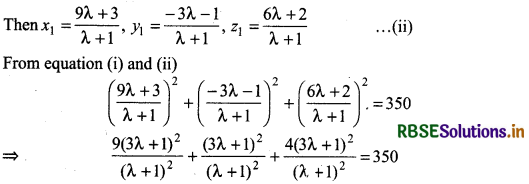
⇒ 14(3λ + 1)² = 350(λ + 1)²
⇒ (3λ + 1)² = 25(λ + 1)²
⇒ 3λ + 1 = ±5(λ + 1)
⇒ 3λ + 1 = 5λ + 5
and 3λ + 1 = - 5λ - 5
⇒ 2λ = - 4
and 8λ = - 6
⇒ λ = - \(\frac{3}{4}\)
Thus, the required ratio is - 3 : 4.

Question 9.
Point P lies on the line joining the points A(7, 2, 1) and B(10, 5, 7). If y-coordinate of P is 4, then find its other coordinates.
Answer:
Let point P(x, y, z). here y = 4 divide the AB in the ratio λ : 1

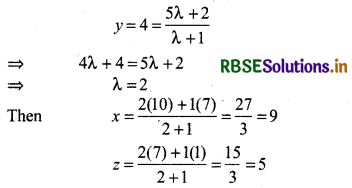
Thus, coordinates of point p are (9, 4, 5)

Question 10.
Find the locus of the points which are equidistant from points A(- 1, 2, 3) and B(3, 2, 1).
Answer:
Let point P(x, y, z) is equidistant from the points A(- 1, 2, 3) and B(3, 2, 1) i.e.
PA = PB
Then PA = distance between the points P(x, y, z) and A(- 1, 2, 3)

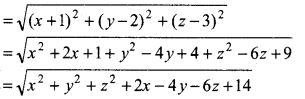
and PB distance between the points P(x, y, z) and B(3, 2, 1)

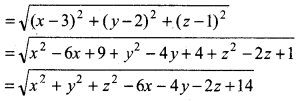
∵ PA = PB (given)
⇒ PA² = PB²
⇒ x² + y² + z² + 2x - 4y - 6z + 14 = x² + y² + z² - 6x - 4y - 2z + 14
⇒ 8x - 4z = 0
⇒ 2x - z = 0,
which is required locus.

Question 11.
FInd the ratio in which line segment joining the point (2, 1, 5) and (3, 4 3) is divided by plane x + y - z = \(\frac{1}{2}\).
Answer:
Let line segment joining the points P(2, 1, 5) and Q(3, 4,3) is divided by point R on plane x + y - z = \(\frac{1}{2}\) in the ratio k : 1.
Then coordinates of points R = \(\left(\frac{3 k+2}{k+1}, \frac{4 k+1}{k+1}, \frac{3 k+5}{k+1}\right)\)
Since, point R lie on plane x + y - z = \(\frac{1}{2}\).
∴ \(\frac{3 k+2}{k+1}+\frac{4 k+1}{k+1}-\frac{3 k+5}{k+1}=\frac{1}{2}\)
⇒ \(\frac{4 k-2}{k+1}=\frac{1}{2}\)
⇒ 8k - 4 = k + 1
⇒ 8k - k = 4 + 1
⇒ 7k = 5
⇒ k = \(\frac{5}{7}\)
Thus, the required ratio = \(\frac{5}{7}\) : 1 = 5 : 7

Question 12.
Using section formula, show that the points A(- 2, 3, 5), B(1, 2, 3) and C(7, 0, - 1) are collinear.
Answer:
Let points C(7, 0, - 1), divides AB in the ratio k : 1.
∴ \(\frac{k-2}{k+1}\) = 7, \(\frac{2 k+3}{k+1}\) = 0 and \(\frac{3 k+5}{k+1}\) = - 1
⇒ k - 2 = 7k + 7, 2k + 3 = 0
and 3k + 5 = - k - 1
⇒ 6k = - 9, 2k = - 3 and 4k = 6
⇒ k = - \(\frac{9}{6}\) = - \(\frac{3}{2}\) and k = - \(\frac{6}{4}\) = - \(\frac{3}{2}\)
Thus, the point C(7, 0, - 1) divides AB in the ratio 3 : 2. i.e., C(7, 0, - 1) divides AB externally in the ratio 3 : 2.
Thus, points A(- 2, 3, 5), B(1, 2, 3) and C(7, 0, - 1) are collinear.

Question 13.
Find the coordinates of those points which trisect the line segment joining the points P(2, 1, - 3) and Q(5, -8, 3).
Answer:
Let M and N are two points which trisect the line segment i.e. in PM, MN and NQ.
So, point M will divide line segment PQ in the ratio 1: 2
and point N will divide line segment PQ in the ratio 2: 1.

Question 14.
Show that points (2, 9, 12), (1, 8, 8) and (- 2, 11, 8) are vertices of an isosceles right triangle and C(- 2, 11,8).
Answer:

∵ AB = BC = 3
and AB² + BC² = (3√2)² + (3√2)²
= 18 + 18 = 36
and AC² = 6² = 36
AC² = AB² + BC² = 2AB²
= 2BC² (∵ AB = BC)
Thus, given points are vertices of an isosceles right triangle.
Hence proved.

Question 15.
If points A(- 1, a, 3), B(3, 0, b) and P(- 3, 3, 0) are collinear.
(i) Find the ratio in which point P(- 3, 3, 0) divides AB
(ii) Find the value of a and b.
Answer:
Let point P(- 3, 3, 0), divides AB in the ratio λ : 1
∴ \(\frac{3 \lambda+1(-1)}{\lambda+1}\) = - 3, \(\frac{0 . \lambda+c}{\lambda+1}\) = 3, \(\frac{b \lambda+3}{\lambda+1}\) = 0
⇒ 3λ - 1 = - 3λ - 3, a = 3λ + 3, bλ + 3 = 0
⇒ 3λ - 1 = - 3λ - 3, a = 3λ + 3, bλ + 3 = 0
λ = -\(\frac{2}{6}=\frac{-1}{3}\), a = 3\(\left(-\frac{1}{3}\right)\) + 3 = - 1 + 3 = 2,
b\(\left(-\frac{1}{3}\right)\) + 3 = 0, b = 9
∴ λ = - \(\frac{1}{3}\), a = 2, b = 9
Thus (i) point P divides AB - 1 : 3 or 1 : 3 externally.

(ii) a = 2, b = 9

Multiple Choice Questions

Question 1.
Point A(5, - 1, 1), B(7, - 4, 7), C(1, - 6, 10) D(- 1, - 3, 4) will be the vertices of a:
(a) Square
(b) Rhombus
(e) Rectangle
(d) None of the above
Answer:
(b) Rhombus

Question 2.
The ratio in which, XY-plane divides the line segment joining the points(- 1, 3, 4) and(2, - 5, 6)
(a) 2 : 3 internally
(b) 2 : 3 Externally
(C) 3 : 2 internally
(d) 3 : 2 Externally
Answer:
(b) 2 : 3 Externally

Question 3.
The triangle formed by the points (0, 7, 10), (- 1, 6, 6) and (- 4, 9, 6) will be:
(a) right triangle
(b isosceles triangle
(c) equilateral triangle
(d) isosecles right triangle
Answer:
(d) isosecles right triangle

Question 4.
The ratio in which, YZ-plane divides the line segment joining the points (2, - 1 - 3) and (3, 2, - 1) is:
(a) - 2 : 3
(b) 3 : - 2
(c) 1 : 2
(d) 2 : 1
Answer:
(a) - 2 : 3

Question 5.
The vertices of a triangle ABC are A(x₁, y₁, z₁) B(x₂, y₂, z₂) and C(x₃, y₃, z₃). Coordinates of its centroid:
(a) \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)
(b) \(\left(\frac{x_1+x_2+x_3}{2}, \frac{y_1+y_2+y_3}{2}, \frac{z_1+z_2+z_3}{2}\right)\)
(c) \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{4}, \frac{z_1+z_2+z_3}{5}\right)\)
(d) None of the above
Answer:
(a) \(\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}, \frac{z_1+z_2+z_3}{3}\right)\)

Question 6.
A(3, 2, 0), B(5, 3, 2), C(- 9, 6, - 3) are the vertices of a triangle ABC. If AD Is angle bisector of ∠BAC, which meets side be at point D, then coordinate of D are
(a) \(\left(\frac{19}{8}, \frac{57}{16}, \frac{17}{16}\right)\)
(b) \(\left(\frac{57}{16}, \frac{19}{8}, \frac{17}{16}\right)\)
(c) \(\left(\frac{17}{16}, \frac{19}{8}, \frac{57}{16}\right)\)
(d) None of the above
Answer:
(a) \(\left(\frac{19}{8}, \frac{57}{16}, \frac{17}{16}\right)\)

Question 7.
The coordinates of any point In YZ-plane are:
(a) (0, y, z)
(b) (0, 0, z)
(c) (0, y, 0)
(d) None of the above
Answer:
(a) (0, y, z)

Question 8.
If the mid-point of sides of a triangle are (1, 5, - 1), (0, 4, - 2) and (2, 3, 4), then vertices of triangle are:
(a) (1, 2, 3), (3, 4, 5), (- 1, 6, - 7)
(b) (2, 3, 1), (5, 3, 4), (- 7, - 1, 6)
(c) (3, 2, 1) (3, 5, 4), (6, - 7, - 1)
(d) None of the above
Answer:
(a) (1, 2, 3), (3, 4, 5), (- 1, 6, - 7)

Question 9.
If point P(3, 2, - 4), Q(5, 4, - 6) and R(9, 8, - 10) are collinear, then ratio in which point R, divides PR is.
(a) 1 : 2
(b) 2 : 1
(c) - 1 : 3
(d) None. of these
Answer:
(a) 1 : 2

Question 10.
The ratio in which plane 2x - 3y + z + 6 = 0 divides the line segment joining the points (2, 4, 16) and (3, 5, - 4) is:
(a) 2 : 1
(b) 1 : 2
(c) 3 : 2
(d) none of the above
Answer:
(a) 2 : 1

Fill in the Blanks

Question 1.
The distances measured from XY-plane upwards in the direction of OZ are taken as .............................. .
Answer:
positive

Question 2.
The distances measured from XY-plane downwards in the direction of OZ’ are taken as ................................... .
Answer:
negative

Question 3.
The point point O is called the .................................... of the coordinate system.
Answer:
origin

Question 4.
The three coordinate planes divide the space Into eight parts known as ......................................
Answer:
octant

Question 5.
The sign of the coordinates of a point determine the octant in which the ...................................... lies.
Answer:
point

Question 6.
The coordinates of any point on the x-axis wilt be as ...................................... .
Answer:
(x, 0, 0)

Question 7.
Point (- 3, 1, 2) lies in ........................... octant.
Answer:
second

Question 8.
The distance between the points P( 1, - 3, 4) and Q(- 4, 1, 2 ) is .............................. .
Answer:
3√5

Question 9.
The YZ-plane divides the line segment formed by joining the points (4, 8, 10) and (6, 10, - 8) in the ratio ................................ .
Answer:
2 : 3

Question 10.
The coordinate of any point in the YZ-plane will be as ............................... .
Answer:
(0, y, z)

True/False

State whether the following statements are true or false:

Question 1.
In three dimensions, the coordinate axes of a rectangle cartesion coordinate system are three mutually perpendicular.
Answer:
True

Question 2.
The the planes determined by the pair of axes are the coordinate planes.
Answer:
True

Question 3.
The three coordinate plane divide the space into nine parts.
Answer:
False

Question 4.
The coordinates of a point P in three dimensional geometry is always written in the form of triplet like (x, y, z).
Answer:
True

Question 5.
The distances are measured to the right ZX-plane and along 0V are taken as negative.
Answer:
False

Question 6.
The distances are measured to the left of ZX-plane and along 'OY’ as positive.
Answer:
False

Question 7.
There is a one to one correspondence between the points in space and ordered triplet (x, y, z) of real numbers.
Answer:
True

Question 8.
Point (- 3, 1, - 2) lies in VI octant.
Answer:
True

Question 9.
Points P(- 2, 3, 5), Q( 1, 2, 3) and R(7, 0, - 1) are collinear.
Answer:
True

Question 10.
We can find the distance between the origin and any point P(x, y, z) by \(\sqrt{x^2+y^2+z^2}\).
Answer:
True