RBSE Class 11 Maths Important Questions Chapter 11 शंकु परिच्छेद

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 11 शंकु परिच्छेद Important Questions and Answers.

RBSE Class 11 Maths Chapter 11 Important Questions शंकु परिच्छेद

अतिलघूत्तरात्मक प्रश्न-

प्रश्न 1.
बिन्दु वृत्त को परिभाषित कीजिए ।
हल:
जब किसी वृत्त की त्रिज्या का मान शून्य हो तो वृत्त का समीकरण होगा-
(x - h)² + (y - k)² = 0
इस प्रकार वृत्त छोटा होता-होता केवल एक बिन्दु मात्र (केन्द्र) रह जाता है तो इसे बिन्दु वृत्त कहते हैं| x² + y² = 0 मूल बिन्दु पर बिन्दु वृत्त का समीकरण होता है।

प्रश्न 2.
समीकरण x² + y² + 2gx + 2fy + c = 0 सदैव एक वृत्त को निरूपित करता है तथा इसका केन्द्र व त्रिज्या लिखिए।
हल:
वृत्त का केन्द्र ( - g, - f) एवं त्रिज्या \(\sqrt{g^2+f^2-c}\)

प्रश्न 3.
उस वृत्त का समीकरण ज्ञात कीजिए, जिसका केन्द्र (a cos θ, a sin θ) एवं त्रिज्या a हो।
हल:
(x - h)² + (y - k)² = (त्रिज्या)²
⇒ (x - a cos θ)² + (y - a sin θ)² = a²
⇒ x² - 2a cos θ . x + a² cos² θ + y² - 2a sin θ y + a² sin² θ = a²
⇒ x² + y² - 2a cos θ x - 2a sin θ y + a² (cos² θ + sin² θ) = a²
⇒ x² + y² - 2a cos θ x - 2a sin θ y = 0

प्रश्न 4.
निम्न वृत्त की केन्द्र व त्रिज्या लिखिए-
(x + 5)² + (y + 1)² = 9
हल:
दिये गये वृत्त की तुलना
(x - h)² + (y - k)² = a²
अतः केन्द्र (- 5, - 1) व त्रिज्या a = 3

प्रश्न 5.
परवलय की नाभीय जीवा किसे कहते हैं ?
हल:
परवलय की ऐसी जीवा जो उसकी नाभि से गुजरे, नाभीय जीवा कहलाती है।

प्रश्न 6.
परवलय की नाभिलम्ब क्या होती है? इसकी लम्बाई का मान लिखिए ।
हल:
परवलय की ऐसी जीवा जो उसकी नाभि से गुजरे और अक्ष के लम्बवत् हो, नाभिलम्ब कहलाती है। परवलय y² = 4ax के नाभिलम्ब की लम्बाई सदैव 4a होती है।

प्रश्न 7.
उस परवलय का समीकरण लिखिये जिसका शीर्ष (0, 0) तथा नाभि (0, - a)
हल:
x² = - 4ay

प्रश्न 8.
दीर्घवृत्त की नाभिलम्ब क्या होती है ? इसकी लम्बाई का मान लिखिये ।
हल:
दीर्घवृत्त की नाभि से गुजरने वाली एवं दीर्घ अक्ष के लम्बवत् जीवा को नाभिलम्ब कहते हैं। इसकी लम्बाई \(\frac{2 b^2}{a}\) होती है।

प्रश्न 9.
दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 की उत्केन्द्रता का सूत्र लिखिये।
हल:
दीर्घवृत्त की उत्केन्द्रता e = \(\sqrt{1-\frac{b^2}{a^2}}\)

प्रश्न 10.
दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 की नियता का समीकरण लिखिये a > b
हल:
x = ± \(\frac{a}{e}\)

प्रश्न 11.
अतिपरवलय \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 के लिये उत्केन्द्रता का मान लिखिये ।
हल:
उत्केन्द्रता (e) = \(\sqrt{1+\frac{b^2}{a^2}}\)

प्रश्न 12.
अतिपरवलय की नियताओं के समीकरण लिखिये |
हल:
-x = ± \(\frac{a}{e}\)

प्रश्न 13.
अतिपरवलय 4x² - 9y² = 36 का शीर्ष लिखिये ।
हल:
4x² - 9y² = 36
या \(\frac{x^2}{9}-\frac{y^2}{4}\) = 1
अतिपरवलय के शीर्ष (± a, 0) = (± 3, 0)

प्रश्न 14.
अतिपरवलय का समीकरण लिखिये जिसकी अनुप्रस्थ अक्ष और संयुग्मी अक्ष क्रमशः 4 तथा 5 है ।
हल:
दिया गया है-
2a = 4, 2b = 5 ∵ b = \(\frac{5}{2}\)
a = 2
(a)² = 4
b² = \(\frac{25}{4}\)
अतः अतिपरवलय का समीकरण होगा-

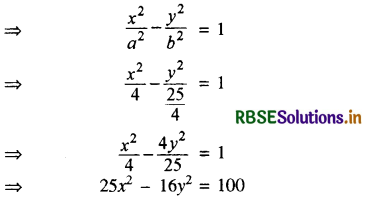
प्रश्न 15.
अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 के एक नाभिलम्ब के सिरों के निर्देशांक लिखिये|
हल:
- (ae, \(\frac{b^2}{a}\)), (ae, -\(\frac{b^2}{a}\))

प्रश्न 16.
अतिपरवलय को परिभाषित कीजिए ।
हल:
"अतिपरवलय उस चलित बिन्दु का बिन्दुपथ है जिसकी दो स्थिर बिन्दुओं ( नाभियों) से दूरियों का अन्तर सदैव अचर होता है।"

प्रश्न 17.
आयतीय अतिपरवलय की उत्केन्द्रता ज्ञात कीजिए ।
हल:
हम जानते हैं कि
b² = a²(e² - 1)
यहाँ b = a अत: a² = a²(e² - 1)
या e² = 2 ⇒ e = √2
अतः आयतीय अतिपरवलय की उत्केन्द्रता √2 होती है।

लघूत्तरात्मक प्रश्न-

प्रश्न 1.
परवलय 9y² - 16x - 12y - 57 = 0 के अक्ष का समीकरण लिखिए।
हल:
दिया गया है-
9y² - 16x - 12y - 57 = 0
⇒ 9y² - 12y = 16x + 57
⇒ 9y² - 12y + 4 = 16x + 57 + 4
⇒ (3y - 2)² = (16x + 61)
माना 3y - 2 = Y तथा 16x + 61 = X
Y² = X
अक्ष का समीकरण Y = 0
∴ 3y - 2 = 0
या 3y = 2

प्रश्न 2.
यदि एक परवलय का समीकरण y² = 8x है तो नाभि के निर्देशांक, अक्ष, नियता का समीकरण और नाभिलम्ब जीवा की लम्बाई ज्ञात कीजिए।
हल:
दिए समीकरण में y का पद है इसलिए परवलय x अक्ष के परितः सममित है।

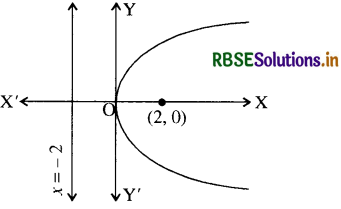
क्योंकि समीकरण में पद x का गुणांक धनात्मक है इसलिए परवलय दाहिनी ओर खुलता है। दिए गए समीकरण y² = 4ax, से तुलना करने पर, a = 2
अतः परवलय की नाभि (2, 0) है और परवलय की नियता का समीकरण x = - 2 है ।
नाभिलम्ब जीवा की लम्बाई 4a = 4 × 2 = 8

प्रश्न 3.
परवलय y² = 8x के अन्तर्गत एक समबाहु त्रिभुज है जिसका एक शीर्ष परवलय का शीर्ष है। त्रिभुज की भुजा की लम्बाई ज्ञात कीजिए।
हल:

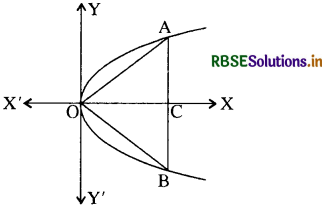
माना कि परवलय y² = 8x के अन्तर्गत एक समबाहु त्रिभुज बनाया गया है तथा इसकी भुजा की लम्बाई P है।
अब ∆ OAC में
OA² = OC² + AC²

प्रश्न 4.
परवलय y² = 18x पर स्थित उस बिन्दु के निर्देशांक ज्ञात कीजिये, जिसकी कोटि भुज की तीन गुना है।
हल:
माना परवलय पर भुज का मान = x₁ है।
∴ परवलय पर कोटि का मान = 3x₁ होगा|
अतः परवलय पर बिन्दु के निर्देशांक होंगे = (x₁, 3x₁)
उपर्युक्त बिन्दु परवलय के समीकरण को सन्तुष्ट करेंगे।
∴ (3x₁)² = 18 × x₁
या 9x₁² = 18x₁
या x₁² = 2x₁
x₁² - 2x₁ = 0
या x₁ (x₁ - 2) = 0
∴ x₁ = 0, 2
∴ कोटि का मान = 3x₁
= 3 × 2 = 6
अतः परवलय पर स्थित बिन्दु के निर्देशांक होंगे = (2, 6)

प्रश्न 5.
परवलय y² = 4ax की एक द्विकोटि की लम्बाई 8a है, सिद्ध कीजिये कि मूल बिन्दु से इस द्विकोटि के शीर्षों को मिलाने वाली रेखायें समकोणीय होंगी।
हल:
दिया गया परवलय का समीकरण
y² = 4ax

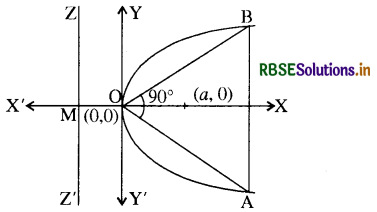
हम जानते हैं, वक्र के अक्ष के लम्बवत् जीवा, वक्र की द्विकोटि कहलाती है।
माना बिन्दु B (h, 4a) तथा (h, - 4a) बिन्दु B परवलय के समीकरण को सन्तुष्ट करेगा,
अतः y² = 4ax
(4a)² = 4a × h
16a² = 4ah
h = 4a
अत: बिन्दु B (4a, 4a) तथा A (4a, - 4a) हमको यहाँ पर ∠B OA = 90° सिद्ध करना है।
OB रेखा का झुकाव (m₁) माना = \(\frac{y_2-y_1}{x_2-x_1}\)
= \(\frac{4 a-0}{4 a-0}\) = 1
इसी प्रकार OA रेखा का झुकाव (m₂) माना
\(\frac{y_2-y_1}{x_2-x_1}\) = - \(\frac{4 a-0}{4 a}\) = - 1
∴ m₁ × m₂ = - 1
∴ द्विकोटि के शीर्ष को मिलाने वाली रेखायें समकोणीय होंगी ।

प्रश्न 6.
दीर्घवृत्त \(\frac{x^2-a x}{a^2}+\frac{y^2-b y}{b^2}\) = 0 के केन्द्र के निर्देशांक लिखिए।
हल:

प्रश्न 7.
अतिपरवलय \(\frac{(x-1)^2}{16}-\frac{(y+2)^2}{9}\) = 1 के केन्द्र के निर्देशांक लिखिए।
हल:
हम जानते हैं अतिपरवलय-
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 का केन्द्र (0, 0) होता है।
∴ x - 1 = 0
∴ x = 1
इसी प्रकार से-
y + 2 = 0
∴ y = - 2
अतः केन्द्र के निर्देशांक = (1, - 2)

निबन्धात्मक प्रश्न

प्रश्न 1.
उस वृत्त का समीकरण ज्ञात करो जो बिन्दुओं (a, a ), (0, a ) a (a, 0) से गुजरता है।
हल:
मान लीजिए कि वृत्त का समीकरण (x - h)² + (y - k)² = r² है।
यह बिन्दुओं (a, a), (0, a) और (a, 0) से गुजरता है। इसलिए हमें प्राप्त होता है कि
(a - h )² + (a - k)² = r² ....................... (1)
(0 - h )² + (a - k)² = r² ....................... (2)
(a - h)² + (0 - k)² = r² ....................... (3)
समीकरण (1) तथा (2) को बराबर करने पर
(a - h)² + (a - k)² = (0 - h)² + (a - k)²
⇒ (a - h)² = h²
∴ a² - 2ah + h² = h² ∴ h = \(\frac{1}{2}\)a
समीकरण (1) तथा (3) को बराबर करने पर
(a - h)² + (a - k)² = (a - h)² + k²
⇒ a² - 2ak + k² = k²
h तथा k का मान समीकरण (1) में रखने पर

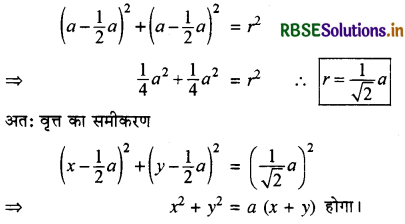
प्रश्न 2.
(x cos α + y sin α - a)² + (x sin α - y cos α - b)² = k² के केन्द्र के निर्देशांक एवं त्रिज्या ज्ञात कीजिए।
हल:
दिये गये वृत्त का समीकरण है-
(x cos α + y sin α - a)² + (x sin α - y cos α - b)² = k²
(x cos α + y sin α)² - 2(x cos a + y sin α) . a + a² + (x sin α - y cos α)² - 2 × (x sin α - y cos α) x b + b2 = k2
⇒ x²(cos² α + sin² α) + y² (sin²α + cos²α) + 2(b cos α - a sin α) . y - 2(a cos α + b sin a) . x + a² + b² - k² = 0
⇒ x² + y² - 2 (a cos α + b sin α) . x - 2(a cos α + b sin α) . x + a² + b² - k² = 0
यहाँ g = - (a cos α - b sin α), f = - (a sin α - b cos α), c = a² + b² - k²
अर्थात् वृत्त का केन्द्र (- g, - f) = [(a cos α + b sin α), (a sin α - b cos α)]
एवं वृत्त की त्रिज्या = \(\sqrt{g^2+f^2-c}\)

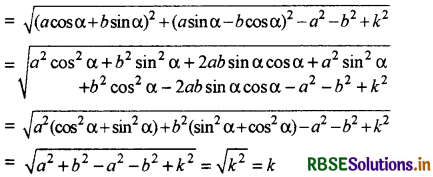
प्रश्न 3.
निर्देश अक्षों को मुख्य अक्ष मानकर दीर्घवृत्त का समीकरण ज्ञात करो जिसका नाभिलम्ब 5 है और उत्केन्द्रता e = \(\frac{2}{3}\) है|
हल:
माना दीर्घवृत्त का समीकरण है-
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 ................. (1)
यहाँ नाभिलम्ब 5 है।

यह दीर्घवृत्त का अभीष्ट समीकरण है।

प्रश्न 4.
उस दीर्घवृत्त की उत्केन्द्रता ज्ञात कीजिये जिसके नाभिलम्ब की लम्बाई उसकी नाभियों की दूरी के बराबर हो।
हल:
माना कि दीर्घवृत्त का समीकरण \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
अत: नाभि F₁ (ae, 0) एवं F₂ (- ae, 0)
नाभियों के बीच की दूरी F₁F₂ = 2ae
नाभिलम्ब की लम्बाई = \(\frac{2 b^2}{a}\)
प्रश्नानुसार, \(\frac{2 b^2}{a}\) = 2ae
b² = a²e ................... (1)
लेकिन b² = a² (1 - e²) ...................... (2)
समीकरण (1) तथा (2) को हल करने पर,
a²e = a² (1 - e²)
⇒ e² + e – 1 = 0

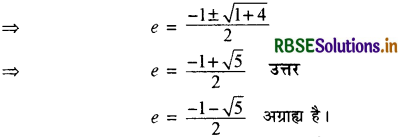
प्रश्न 5.
उस दीर्घवृत्त की उत्केन्द्रता ज्ञात कीजिये जिसकी लघु अक्ष उसकी नाभियों की दूरी के बराबर है तथा केन्द्र, मूल बिन्दु पर और अक्ष, निर्देश अक्षों के संपाती हो ।
हल:
माना कि दीर्घवृत्त का समीकरण \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 है।
अत: नाभि F₁ (ae, 0) एवं F₂ ( - ae, 0) एवं लघु अक्ष = 2b
नाभियों के बीच की दूरी F₁ F₂ = 2 ae
प्रश्नानुसार, 2ae = 2b

प्रश्न 6.
उस दीर्घवृत्त का समीकरण ज्ञात कीजिये जिसके शीर्ष एवं नाभियों के निर्देशांक क्रमश: (± 5, 0) तथा (± 4, 0) हों।
हल:
दीर्घवृत्त का समीकरण है-
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
इसके शीर्ष तथा नाभियों के निर्देशांक क्रमश: (±a, 0) तथा (± ae, 0) हैं। दिये गये निर्देशांकों से तुलना करने पर,
अतः ± a = ± 5
∴ a = 5
तथा ± ae = ± 4
∴ ae = 4
लेकिन a = 5
∴ 5 × e = 4

प्रश्न 7.
उस अतिपरवलय का समीकरण ज्ञात कीजिये जिसका नाभिलम्ब 8 है तथा संयुग्मी अक्ष नाभियों के बीच की दूरी की आधी है।
हल:
प्रश्नानुसार नाभिलम्ब 8 ⇒ \(\frac{2b^2}{a}\)
b² = 4a ............ (1)
एवं संयुग्मी अक्ष
2b = \(\frac{1}{2}\) (2ae) = ae.
2b = ae ..................... (2)
हम जानते हैं- b² = a² (e² - 1)
समीकरण (1) से 4a = a² (e² - 1)
⇒ e² = \(\frac{4}{a}\) + 1 ...................... (3)
समीकरण (2) का वर्ग करके समीकरण (1) से b² का मान रखने पर
4 × (4a) = a²e²
⇒ e² = \(\frac{16}{a}\) ........................... (4)
समीकरण (3) तथा (4) से

प्रश्न 8.
यदि एक अतिपरवलय तथा इसके संयुग्मी अतिपरवलय की उत्केन्द्रतायें क्रमशः e तथा e' हों तो सिद्ध कीजिये कि
\(\frac{1}{e^2}+\frac{1}{\left(e^{\prime}\right)^2}\) = 1
हल:
माना अतिपरवलय का समीकरण है-

बहुचयनात्मक प्रश्न-

प्रश्न 1.
उस वृत्त का समीकरण क्या होगा जिसकी त्रिज्या a और केन्द्र (0, 0) हो-
(A) x² - y² = a²
(B) x² + y² = ²
(C) y² - x² = a²
(D) x² + y² + a² = 0
हल:
(B) x² + y² = ²

प्रश्न 2.
उस वृत्त का समीकरण क्या होगा जिसके केन्द्र (- 3, 2) और त्रिज्या 4 हैं?
(A) (x - 3)² + (y + 2)² = 16
(B) (x + 3)² +( y - 2)² = 16
(C) (y + 2)² - (x - 3)² = 16
(D) (x - 3)² - (y + 2)² = 16
हल:
(B) (x + 3)² +( y - 2)² = 16

प्रश्न 3.
वृत्त x² + y² - 10x + 16y + 6 = 0 का केन्द्र होगा-
(A) (0, 5)
(B) (5, 0)
(C) (5, - 8)
(D) (8, - 5)
हल:
(C) (5, - 8)

प्रश्न 4.
यदि (x, 3) (3, 5) किसी वृत्त के व्यास के सिरे हैं जिसका केन्द्र (2, y) है तो x और y के मान हैं
(A) x = 1, y = 4
(B) x = 4, y = 1,
(C) x = 5/2, y = 1
(D) x = 8, y = 2
हल:
(A) x = 1, y = 4

प्रश्न 5.
परवलय x² = - 18y की नियता का समीकरण है-
(A) y = - 2
(B) y = 2
(C) x = 2
(D) x = - 2
हल:
(B) y = 2

प्रश्न 6.
परवलय x² = - 8y की नाभि है-
(A) (2, 0)
(B) (0, 2)
(C) (- 2, 0)
(D) (0, - 2)
हल:
(D) (0, - 2)

प्रश्न 7.
एक शांकवीय परिच्छेद परवलय होगा, यदि -
(A) e = 0
(B) e < 1 (C) e > 1
(D) e = 1
हल:
(D) e = 1

प्रश्न 8.
परवलय y² = 12x की नियता का समीकरण होगा-
(A) x = 3
(B) y = 3
(C) x = - 3
(D) y = - 3
हल:
(C) x = - 3

प्रश्न 9.
यदि परवलय x² = 8y की द्विकोटि की लम्बाई 8 है तो इसके सिरे होंगे-
(A) (4, 2), (4, - 2)
(B) (2, 4), (2, - 4)
(C) (4, 2), (- 4, 2)
(D) (- 2, - 4), (2, 4)
हल:
(B) (2, 4), (2, - 4)

प्रश्न 10.
यदि किसी परवलय का शीर्ष मूल बिन्दु हो तथा नियता y + 4 = 0 हो तो उसका समीकरण होगा-
(A) y² = 16x
(B) x² = 16y
(C) x² = - 16y
(D) y² = - 16x
हल:
(B) x² = 16y

प्रश्न 11.
परवलय x² + 12y = 0 के नाभिलम्ब का समीकरण है-
(A) y + 12
(B) y - 12
(C) y - 3 = 0
(D) y + 3 = 0
हल:
(D) y + 3 = 0

प्रश्न 12.
यदि परवलय y² = 4ax बिन्दु (- 3, 2) से गुजरे तो इसके नाभिलम्ब की लम्बाई-
(A) \(\frac{4}{3}\)
(B) \(\frac{4}{5}\)
(C) \(\frac{1}{3}\)
(D) 5
हल:
(A) \(\frac{4}{3}\)

प्रश्न 13.
परवलय x² = 4ay की नियता का समीकरण होगा-
(A) x + a = 0
(B) x - a = 0
(C) y + a = 0
(D) y - a = 0
हल:
(C) y + a = 0

प्रश्न 14.
एक शांकवीय परिच्छेद दीर्घवृत्त होगा, यदि -
(A) e = 0
(B) e < 1 (C) e > 1
(D) e = 1
हल:
(B) e < 1 प्रश्न 15. दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (b > a ) के नाभिकों के निर्देशांक होंगे-
(A) (± ae, 0)
(B) (± be, 0)
(C) (0, ± ae)
(D) (0, ± be)
हल:
(D) (0, ± be)

प्रश्न 16.
आयतीय अतिपरवलय की उत्केन्द्रता होगी-
(A) 0
(B) 1
(C) √2
(D) 2
हल:
(C) √2

प्रश्न 17.
अतिपरवलय 9x² - 16y² = 144 की उत्केन्द्रता होगी -
(A) 1
(B) 0
(C) \(\frac{5}{16}\)
(D) \(\frac{5}{4}\)
हल:
(D) \(\frac{5}{4}\)

प्रश्न 18.
अतिपरवलय x² - 4y² = 4 के नाभिलम्ब की लम्बाई होगी-
(A) 4
(B) \(\frac{1}{4}\)
(C) 1
(D) 2
हल:
(C) 1

प्रश्न 19.
अतिपरवलय 4x² - 9y² = 36 के नाभियों के निर्देशांक होंगे-
(A) (±√13, 0)
(B) (0, ±√13)
(C) (+\(\frac{\sqrt{13}}{3}\), 0)
(D) (0, ±\(\frac{\sqrt{13}}{3}\))
हल:
(A) (±√13, 0)

प्रश्न 20.
एक शांकवीय परिच्छेद अतिपरवलय होगा यदि—
(A) e = 0
(B) e < 1 (C) e > 1
(D) e = 1
हल:
(C) e > 1

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
दीर्घवृत्त की उत्केन्द्रता, दीर्घवृत्त के केन्द्र से ............................. और केन्द्र से शीर्ष की दूरियों का अनुपात है।
हल:
केन्द्र

प्रश्न 2.
एक वृत्त, तल के उन बिन्दुओं का समुच्चय है जो तल के एक स्थिर बिन्दु से .............................. दूरी पर होते हैं।
हल:
समान

प्रश्न 3.
नाभि (a, 0), a > 0 और नियता x = a वाले परवलय का समीकरण .......................... है।
हल:
y² = 4ax

प्रश्न 4.
परवलय y² = 4ax के नाभिलम्ब जीवा की लम्बाई ................................... है।
हल:
4a

प्रश्न 5.
दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 के नाभिलम्ब जीवा की लम्बाई ................................ है।
हल:
\(\frac{2 b^2}{a}\)

प्रश्न 6.
एक अतिपरवलय तल के उन सभी बिन्दुओं का समुच्चय है जिनकी तल में दो स्थिर बिन्दुओं से दूरी का अन्तर ................................... होता है।
हल:
अचर

प्रश्न 7.
x - अक्ष पर नाभि वाले अतिपरवलय का समीकरण .................................... है|
हल:
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1

प्रश्न 8.
अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = - 1 के नाभिलम्ब जीवा की लम्बाई .................................... है|
हल:
\(\frac{2 a^2}{b}\)

प्रश्न 9.
समीकरण x² + y² + 2x + 4y + 5 = 0 एक ................................ का समीकरण है।
हल:
वृत्त

प्रश्न 10.
परवलय (y + a)² = 8a (x - a ) के शीर्ष .............................. हैं।
हल:
(a, - a)

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
परवलय y² = 4ax की नाभि के निर्देशांक (-a, 0) हैं।
हल:
सत्य

प्रश्न 2.
परवलय x² = 4ay की नियता का समीकरण y = a
हल:
असत्य

प्रश्न 3.
परवलय x² = - 4ay की अक्ष का समीकरण y = 0 है।
हल:
असत्य

प्रश्न 4.
दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a > b हेतु उत्केन्द्रता e = \(\sqrt{1-\frac{b^2}{a^2}}\) होती है।
हल:
सत्य

प्रश्न 5.
दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a > b हेतु लघु अक्ष x = 0 है।
हल:
असत्य

प्रश्न 6.
दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a > b की नाभिलम्ब जीवा की लम्बाई \(\frac{2 b^2}{a}\) है।
हल:
सत्य

प्रश्न 7.
अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 की उत्केन्द्रता e = \(\sqrt{\frac{a^2+b^2}{a^2}}\) होती है।
हल:
सत्य

प्रश्न 8.
अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = -1 की नाभिलम्ब जीवा की लम्बाई \(\frac{2 b^2}{a}\) है।
हल:
असत्य

प्रश्न 9.
अतिपरवलय 9x² - 16y² = 144 की उत्केन्द्रता \(\frac{\sqrt{5}}{4}\) है।
हल:
असत्य

प्रश्न 10.
वृत्त x² + y² - 4x + 6y – 51 = 0 का केन्द्र (2, - 3) है।
हल:
सत्य

सही मिलान कीजिए-

भाग (A)	भांग (B)
1. परवलय x2 = 4ay की नाभिलम्ब जीवा की लम्बाई	(a) y = 0
2. दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a > b की दीर्घ अक्ष की लम्बाई	(b) \(\frac{2 a^2}{b}\)
3. अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 के शीर्ष के निर्देशांक	(c) y = b/e, y = -b/e
4. किसी त्रिभुज का केन्द्रक (2, 7) हो तथा दो शीर्ष ( 4, 8) व (-2, 6) होने पर तीसरा शीर्ष	(d) (0, ±be)
5. परवलय y2 = - 4ax की नाभि के निर्देशांक	(e) 4a
6. अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = - 1 के नाभि के निर्देशांक	(f) (-g, -f)
7. दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1  a > b के दीर्घ अक्ष का समीकरण	(g) (±a, o)
8. अतिपरवलय \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = - 1 की नाभिलम्ब की लम्बाई	(h) (- a, 0)
9. वृत्त x2 + y2 + 2gx + 2fy + c = 0 के केन्द्र के निर्देशांक	(i) 2b
10. दीर्घवृत्त \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, a < b के दीर्घ अक्ष की लम्बाई	(j) 2a

हल:
1. (e)
2. (j)
3. (g)
4. (c)
5. (h)
6. (d)
7. (a)
8. (f)
9. (b)
10. (i)