RBSE Class 11 Maths Important Questions Chapter 11 Conic Sections

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 11 Conic Sections Questions and Answers.

RBSE Class 11 Maths Chapter 11 Important Questions Conic Sections

Question 1.
The focus of a parabolic mirror is at a distance of 7 cm from its vertex. If the mirror is 63 cm deep, find the diameter of the mirror.
Answer:
A parabolic mirror is shown in the following figure. Its vertex is origin O(0, 0).
Coordinates of focus F = (a, 0) = (7, 0)
[Since, focus is at a 7 cm distance from vertex]
Depth of mirror = OP = 63cm

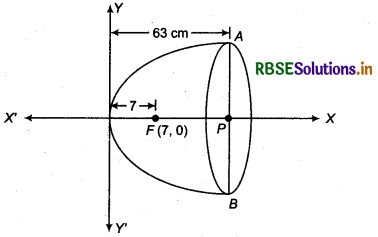
We have to find diameter AB of the mirror.
∴ Parabola is symmetric about x-axis.
Standard equation of parabola y² = 4ax
Here, a = 7, then y² = 4(7)x
⇒ y² = 28x ....................... (1)
Again, putting x = 63 in equation (1),
y² = 28 × 63
⇒ y = \(\sqrt{28 \times 63}\)
⇒ y = 42
Coordinates of B = (63, - 42)
Diameter of mirror
AB = \(\sqrt{(63-63)^2+\{42-(-42)\}^2}\)
= \(\sqrt{0^2+84^2}\) = 84
Thus, diameter of mirror = 84 cm

Question 2.
A beam is supported at its ends by supports which are 18 metres apart. Since the load is concentrated at its center, there is a diflection of 5 cm at the centre and the deflected beam is in the shape of a parabola. How far from the centre is the deflection 2 cm?
Answer:

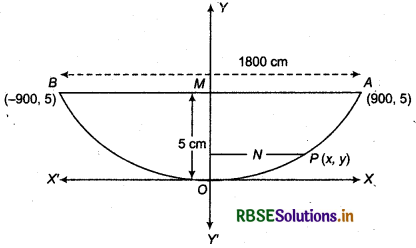
According to figure, AB is a rod.
Let the vertex be at the lowest point O, which lies on origin.
Let coordinates of one end of rod A be (900, 5) and of other end B be (- 900, 5).
The line, passes through base A and B lies at point N, below 2 cm from M(mid point of AB).
Let P(x, y) be any point on deflected beam which is below 2 cm from line AB.
Now, we have to find that at what distance, from M (centre of beam) point P(x, y) lies?
Again, 0M = 5 cm, and MN = 2 cm
ON = OM - MN = (5 - 2) = 3 cm
Then coordinates of point P at deflected beam (parabola) be (x, 3).
Again, parabola is symmetric about y-axis.
Then standard equation of parabola x² = 4ay
Since, parabola passes through point (900,5), then
(900)² = 4a × 5
⇒ a = \(\frac{900 \times 900}{4 \times 5}\) = 40500 cm
Again, parabola also passes through the point P(x, 3)
then x² = 4 × a × 3
= 4 × 40500 × 3
⇒ x² = 486000cm
⇒ x = \(\sqrt{486000}\) cm
= \(\sqrt{4 \times 4 \times 5 \times 5 \times 9 \times 9 \times 5 \times 3}\)
= 4 × 5 × 9\(\sqrt{5 \times 3}\) = 180√15 cm
Thus, deflection of 2 cm will be from the centre.

Question 3.
A rod of length 20 cm rests between two coordinate axis in such a way that the end point A lies on x-axis and end point B lies on y-xis. A point is taken on the rod in such a way that it is at a distance of 9 cm from the lower part. Prove that the locus of this point is an ellipse.
Answer:

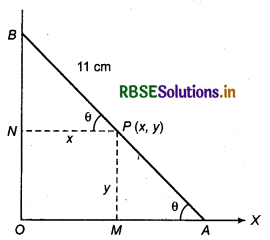
As shown in figure, let rod AB rests in between two axis whose lower end A is at x-axis and upper end B is at y-axis. Point P lies on rod, whose length from point A (from lower end) is 9 cm. i.e. AP= 9 cm then BP = 11 cm (AB = 20cm)

Let the coordinates of point P be (x, y).
Now, from point P draw perpendiculars PM and PN respectively on OX and OY.
If rod makes angle θ with x-axis, then
∠MAP = θ and ∠NPB = θ
In right ∆ AMP,

which is an ellipse.
Thus, locus of a point P is an ellipse.
Hence proved.

Question 4.
Let x = (v cos α)t, y = (v sin α)t - \(\frac{1}{2}\)gt² are respectively x and y coordinates in XY-plane of any points P where t ¡s arbitrary constant and g, v, α are constant. Show that locus of point P is a parabola. Also, write its vertex.
Answer:

Question 5.
Find the point on parabola y² = 8k whose focal distance is 4. If focal distance is 8 then what ‘will be the coordinates of point.
Answer:
Let (x, y) be coordinates of any point on parabola.
Then its distance from focus.
SP = a + x
∴ 4 = 2 + x (4a = 8 ⇒ a = 2)
∴ x = 2
Thus, y² = 8x = 8 × 2 = 16
⇒ y = ±4
Thus, coordinates of point = (2, ±4)
In second case, when distance from focus is 8.
Then, SP=a+x
∴ 8 = 2 + x
⇒ x = 6
Now, y² = 8x
⇒ y² = 8 × 6 = 48
⇒ y = ±4√3
Thus, the coordinate of point = (6, ± 4√3)

Question 6.
The distance of a point on ellipse from centre of ellipse \(\frac{x^2}{6}+\frac{y^2}{2}\) = 1 is 2. Find eccentric angle of that point.
Answer:
Any point on ellipse P(√6 cos Φ, √2 sin Φ) is at a distance of 2 from centre of ellipse O(0, 0).
∴ \(\sqrt{(\sqrt{6} \cos \phi-0)^2+(\sqrt{2} \sin \phi-0)^2}\) = 2
⇒ 6 cos²Φ + 2 sin²Φ = 4
⇒ 3 cos²Φ + sin²Φ = 2
⇒ 3 cos²Φ + 1 - cos²Φ = 2
⇒ 2 cos²Φ = 1
⇒ cos Φ = ± \(\frac{1}{\sqrt{2}}\)
Φ = \(\frac{\pi}{4}\) or \(\frac{3 \pi}{4}\)
Thus, required angle = \(\frac{\pi}{4}\) or \(\frac{3 \pi}{4}\)

Multiple Choice Questions

Question 1.
Equation of circle passing through origin and with centre (a, b) is:
(a) x² + y² - 2ax - 2by = 0
(b) x² - y² + 2ax + 2by = 0
(c) x² + y² + 2ax + 2by = 0
(d) None of these
Answer:
(a) x² + y² - 2ax - 2by = 0

Question 2.
Equation of circle passing through the point (3, 6) and centre (2, - 1) is:
(a) x² + y² + 4x + 2y - 45 = 0
(b) x² + y² - 4x - 2y + 45 = 0
(c) x² + y³ - 4x - 2y - 45 = 0
(d) None of these
Answer:
(a) x² + y² + 4x + 2y - 45 = 0

Question 3.
Any point of circle x² + y² = a² can be taken as:
(a) (a cos θ, a sin θ)
(b) (a cos θ, b sin θ)
(e) (a sin θ, b cos θ)
(d) None of these
Answer:
(a) (a cos θ, a sin θ)

Question 4.
Equation of circle with radius S and centre (- 4, 6) is:
(a) (x + 4)² + (y - 6)² = 25
(b) (x - 4)² + (y + 6)² = 25
(c) (x + 4)² + (y + 16)² = 25
(d) None of these
Answer:
(a) (x + 4)² + (y - 6)² = 25

Question 5.
Centre of circle x² + y² + 4x + 8y - 5 = 0 is:
(a) (- 2, - 4)
(b) (2, 4)
(c) (- 2, 4)
(d) None of these
Answer:
(a) (- 2, - 4)

Question 6.
The radius of circle x² + y² + 8x + 4y - 5 = 0 is:
(a) 5 units
(b) 6 units
(c) 8 units
(d) None of these
Answer:
(a) 5 units

Question 7.
The centre of a circle lies at x-axis at a distance of 6 units form origin. If radius of circle ¡s 3 units then equation of circle is:
(a) x² + y² - 12x + 27 = 0
(b) x² + y² + 12x + 27 = 0
(c) x² + y² + 12x - 27 = 0
(d) None of these
Answer:
(a) x² + y² - 12x + 27 = 0

Question 8.
Equation of circle passing through the points (0, 0) and (2, 4) and centre of line x + y = 4 is:
(a) (x - 3)² + (y - 1)² = 10
(b) (x + 3)² + (y + 1)² = 10
(c) (x + 3)² + (y - 1)² = 10
(d) None of these
Answer:
(a) (x - 3)² + (y - 1)² = 10

Question 9.
Equation of circle with centre (- a, - b)and radius (\(\sqrt{a^2-b^2}\)) is:
(a) x² + y² + 2ax + 2by + 2b² = 0
(b) x² + y² - 2ax - 2by - 2b² = 0
(c) x² + y² - 2ax - 2by + 2b² = 0
(d) None of these
Answer:
(a) x² + y² + 2ax + 2by + 2b² = 0

Question 10.
Equation of circle passes through points (0, 0) and cut intercepts a and b with axis is:
(a) x² + y² - ax - by = 0
(b) x² + y² + ax + by = 0
(c) x² + y² - ax + by = 0
(d) None of these
Answer:
(a) x² + y² - ax - by = 0

Question 11.
Equation of circle with centre (1, - 3) and touches the line 2x - y - 4 = 0 is:
(a) x² + y² - 2x + 6y + \(\frac{49}{5}\) = o
(b) x² + y² + 2x - 6y + \(\frac{49}{5}\) = 0
(c) x² + y² + 2x - 6y - \(\frac{49}{5}\) = 0
(d) None of these
Answer:
(a) x² + y² - 2x + 6y + \(\frac{49}{5}\) = o

Question 12.
Equation of circle passes through point (6, 3) and touches the two axis, is:
(a) x² + y² - 6x - 6y + 9 = 0,
x² + y² - 30x - 30y + 225 = 0
(b) x² + y² - 6x + 6y + 9 = 0,
x² + y² - 30x + 30y + 225 = 0
(c) x² + y² + 6x - 6y + 9 = 0,
x² + y² + 6x - 6y + 9 = 0,
x² + y² + 30x - 30y - 225 = 0
(d) None of these
Answer:
(a) x² + y² - 6x - 6y + 9 = 0,
x² + y² - 30x - 30y + 225 = 0

Question 13.
Equation of circle touching the lines x = 0, y = 0 and x = a is:
(a) x² + y² ± ax ± ay + \(\frac{a^2}{4}\) = 0
(b) x² + y² ± ax ± ay - \(\frac{a^2}{4}\) = 0
(c) x² + y² ± ax ± ay + a² = 0
(d) None of these
Answer:
(a) x² + y² ± ax ± ay + \(\frac{a^2}{4}\) = 0

Question 14.
Centre of circle passes through the points (1, 0), (0, -6) and (3, 4) is :
(a) \(\left(-\frac{71}{4}, \frac{47}{8}\right)\)
(b) \(\left(-\frac{71}{8}, \frac{47}{8}\right)\)
(c) \(\left(-\frac{71}{8},-\frac{47}{8}\right)\)
(d) None of these
Answer:
(a) \(\left(-\frac{71}{4}, \frac{47}{8}\right)\)

Fill in the Blanks

Question 1.
The vertex separates the cone into two parts called .............................. .
Answer:
nappes

Question 2.
If we take the intersection of a plane with a cone, the section so obtained is called a .................................. .
Answer:
conic section

Question 3.
When 0 ≤ β < α; the plane cuts through both the nappes and the curves of intersection is a ..............................
Answer:
hyperbola

Question 4.
The centre of the circle x² + y² = r² is ...................................
Answer:
(0, 0)

Question 5.
The point of intersection of parabola with the axis is called the .........................................
Answer:
vertex

Question 6.
...................................... are the coordinates of the focus of the parabola y² = 8x.
Answer:
(2, 0)

Question 7.
...................................................... is the equation of the parabola with vertex at (0, 0) and focus at (0, 2).
Answer:
x² = 8y

Question 8.
An ..................................... is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
Answer:
ellipse

Question 9.
The end points of the major axis are called the ........................................... of the ellipse.
Answer:
vertices

Question 10.
The line through the centre and perpendicular to the transverse axis is called the ..............................................
Answer:
conjugate

True/False

State whether the following statements are true or false.

Question 1.
The coordinates of the centre of the circle (x + 3)² + (y - 2)² = 16 are (3, - 2).
Answer:
False

Question 2.
The radius of the circle x² + y² + 8x + 10y - 8 = 0 is 7.
Answer:
True

Question 3.
A line through the focus and perpendicular to the directrix is called the focus of the parabola.
Answer:
False

Question 4.
When the axis of symmetry is along the x-axis the parabola opens to the right if the coefficient of x is positive.
Answer:
True

Question 5.
When the axis of symmetry is along the y-axis the parabola opens downwards if the coefficient of y is negative.
Answer:
True

Question 6.
The end points of the major axis are called the focii of the ellipse.
Answer:
False

Question 7.
Eccentricity of an ellipse is greater than 1.
Answer:
False

Question 8.
The points at which the hyperbola intersects the transverse axis are called the vertices of the hyperbola.
Answer:
True

Question 9.
Eccentricity of the hyperbola is less than 1.
Answer:
False

Question 10.
The length of the latus rectum in hyperbola is \(\frac{2 b^2}{a}\).
Answer:
False