RBSE Class 11 Maths Important Questions Chapter 10 सरल रेखाएँ

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 10 सरल रेखाएँ Important Questions and Answers.

RBSE Class 11 Maths Chapter 10 Important Questions सरल रेखाएँ

अतिलघूत्तरात्मक प्रश्न-

प्रश्न 1.
जब दो रेखाओं में से एक रेखा x-अक्ष के समान्तर हो, तो उन दोनों रेखाओं के बीच का कोण क्या होगा, जो कि द्वितीय रेखा x- अक्ष से बनाती है?
हल:
माना कि प्रथम रेखा की समीकरण
y = Const.
माना कि द्वितीय रेखा की समीकरण
y = mx + c
यदि दूसरी रेखा x-अक्ष से θ कोण बनाये तो
m = tan θ ⇒ θ = tan^-1 (m)
∴ दोनों रेखाओं के बीच का कोण = tan^-1 (m)

प्रश्न 2.
- 3x + 2y + 4 = 0 के लम्बवत् रेखा की समीकरण लिखिये
हल:
दिया गया समीकरण
- 3x + 2y + 4 = 0
सर्वप्रथम दी गई समीकरण में (-ve Common) लेने पर रेख की समीकरण होगी
3x - 2y - 4 = 0 उत्तर
अब इसके लम्बवत् रेखा 2x + 3y + λ = 0

प्रश्न 3.
सरल रेखा 3x - 4y + 5 = 0 पर बिन्दु (2, 3) से डाले गये लम्ब की लम्बाई ज्ञात कीजिए ।
हल:

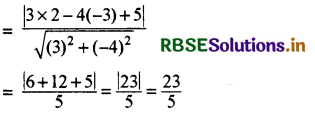
प्रश्न 4.
रेखा y = mx + c पर बिन्दु (4, 5) से डाले गये लम्ब की लम्बाई ज्ञात कीजिये।
हल:
यहाँ पर रेखा का समीकरण mx - y + c = 0
लम्ब की लम्बाई = \(\frac{|m \times 4-5+c|}{\sqrt{m^2+1}}\)
∴ लम्ब की लम्बाई = \(\frac{|4 m-5+c|}{\sqrt{m^2+1}}\)

प्रश्न 5.
समान्तर रेखाओं 2x + 3y + 4 = 0 के बीच की दूरी लिखिये।
हल:
समान्तर रेखाओं के बीच की दूरी

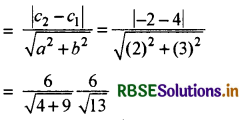
प्रश्न 6.
समान्तर रेखाओं 3x - 4y + 2 = 0 एवं 6x - 8y + 3 = 0 के बीच की दूरी बताइये|
हल:
यहाँ रेखाओं के समीकरणों में x तथा y के संगत गुणांक समान नहीं हैं।
अतः प्रथम रेखा के समीकरण में 2 का गुणा करने पर अब दी गयी
रेखायें
6x - 8y + 4 = 0 ................. (1)
6x - 8y + 3 = 0 .................. (2)
∴ इनके बीच की दूरी = \(\frac{|4-3|}{\sqrt{(6)^2+(8)^2}}\) = \(\frac{1}{\sqrt{100}}\)
= \(\frac{1}{10}\)

प्रश्न 7.
रेखा 3x - 5y + 7 = 0 के लम्बवत् एवं बिन्दु (1, 5) से गुजरने वाली रेखा का समीकरण बताइये।
हल:
दी गयी रेखा के लम्बवत् रेखा का समीकरण
5x + 3y + λ = 0
यह रेखा बिन्दु (1, 5) से गुजरती है
∴ 5 × 1 + 3 × 5 + λ = 0
5 + 15 + λ = 0
λ = - 20
अभीष्ट रेखा का समीकरण 5x + 3y - 20 = 0

प्रश्न 8.
यदि बिन्दु P (1, 2), Q (- 1, x) एवं R (2, 3) संरेख हैं तो x का मान बताइए।
हल:
तीनों बिन्दु संरेख हैं।
इसलिए PQ का ढाल = QR का ढाल

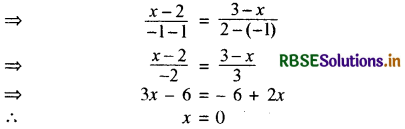
प्रश्न 9.
बिन्दु (- 4, - 3) से होकर जाने वाली सरल रेखा का समीकरण लिखिए जो x अक्ष के समानान्तर है।
हल:
प्रश्नानुसार प्रवणता
m = 0, x₁ = - 4,
y₁ = - 3
अतः सरल रेखा का समीकरण
y - y₁ = m(x - x₁)
⇒ y + 3 = 0 (x + 4)
⇒ y + 3 = 0 ∴ y = - 3

प्रश्न 10.
उस सरल रेखा का समीकरण ज्ञात कीजिए जो अक्षों से समान तथा धन अन्तःखण्ड काटती है।
हल:
जब कोई रेखा x - अक्ष से a इकाई और y-अक्ष से b इकाई का अन्तः खण्ड काटती है तब उसका समीकरण \(\frac{x}{a}+\frac{y}{b}\) = 1 होता है। लेकिन b = a दिया है।
∴ समीकरण \(\frac{x}{a}+\frac{y}{a}\) या x + y = a

लघुत्तरात्मक प्रश्न

प्रश्न 1.
उस सरल रेखा की समीकरण ज्ञात कीजिये जो कि x- अक्ष से 'a' अंतःखण्ड काटती है और उसके साथ x कोण बनाती है ।
हल:
रेखा x - अक्ष से x कोण बनाती है α
∴ m = tan α रेखा की समीकरण y = mx + c
द्वारा यहाँ रेखा की समीकरण y = tan α . x + c
दोनों तरफ c का भाग देने पर

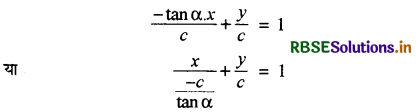
प्रश्नानुसार x- अक्ष पर काटा गया अंत: खण्ड
a = \(\frac{-c}{\tan \alpha}\) ⇒ c = - a tan α
अभीष्ट रेखा का समीकरण
У = tan α . x - a tan α
y = tan α (x - α)

प्रश्न 2.
उस सरल रेखा का समीकरण ज्ञात कीजिये जो रेखाओं 2x + y = 3 एवं 3x + 4y = 7 के प्रतिच्छेद बिन्दु से गुजरे एवं अक्षों से बराबर अंत: खण्ड काटे।
हल:
दी गई रेखाएँ 2x + y = 3 तथा 3x + 4y = 7 हैं। रेखाओं के प्रतिच्छेद बिन्दु निकालने पर
2x + y = 3 .................. (1)
3x + 4y = 7 .................. (2)
समीकरण (1) में 3 से गुणा करने और समीकरण (2) में 2 से गुणा करने पर

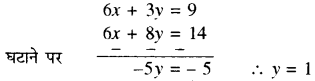
समीकरण (1) में मान रखने पर x = 1
अतः प्रतिच्छेद बिन्दु (1, 1) होगा।
अब अंत: खण्ड रूप में रेखा का समीकरण
\(\frac{x}{a}+\frac{y}{a}\) = 1
∵ रेखा अक्षों पर बराबर अंतः खण्ड काटती है
∴ a = b ⇒ \(\frac{x}{a}+\frac{y}{b}\) = 1 ⇒ x + y = a
x + y = a ............... (3)
प्रश्नानुसार रेखा (3) बिन्दु (1, 1) से गुजरती है।
अतः यह बिन्दु रेखा को संतुष्ट करेगा।
⇒ 1 + 1 = a ⇒ a = 2
∴ अभीष्ट रेखा का समीकरण x + y = 2

प्रश्न 3.
उस रेखा का समीकरण ज्ञात कीजिये जो बिन्दु (-4, 5) से होकर जाती है और अक्षों पर बराबर एवं विपरीत चिह्न के अंतः खण्ड काटती है।
हल:
माना कि सरल रेखा का अभीष्ट समीकरण है
\(\frac{x}{a}+\frac{y}{b}\) = 1 .......... (1)
जबकि रेखा द्वारा x - अक्ष एवं y - अक्ष पर काटे गये अंत: खण्ड क्रमश: a, b हैं।
प्रश्नानुसार रेखा अक्षों से बराबर एवं विपरीत चिह्न वाले अंत: खण्ड काटती है ।
अतः b = - a इस प्रकार रेखा का समीकरण होगा-
\(\frac{x}{a}+\frac{y}{-a}\) = 1
x - y = a ....... (2)
समीकरण (2) की रेखा (- 4, 5) से गुजरती है। अतः यह निर्देशांक समीकरण (2) में संतुष्ट करने पर
- 4 - 5 = a ∴ a = - - 9
समीकरण (2) में मान रखने पर
x - y = - 9 ∴ x - y + 9 = 0
अतः अभीष्ट समीकरण x - y + 9 = 0 होगी।

प्रश्न 4.
सिद्ध कीजिये कि रेखायें 7x - 5y + 20 = 0 तथा 5x + 7y + 19 = 0 एक-दूसरे पर लम्ब हैं।
हल:
दी गयी पहली रेखा का समीकरण
7x - 5y + 20 = 0
इसकी प्रवणता

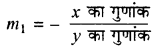
m₁ = - \(\frac{7}{(-5)}=\frac{7}{5}\) ................. (1)
इसी प्रकार से दूसरी रेखा का समीकरण 5x + 7y + 19 = 0
इसकी प्रवणता m₂ हो तब

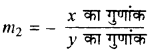
= - \(\frac{5}{7}\) .................. (2)
हम जानते हैं कि यदि दो रेखाओं की प्रवणतायें m₁ तथा m₂ हों और वे परस्पर लम्बवत् हों तो उनकी प्रवणताओं का गुणनफल सदैव - 1 होता है।
अर्थात् m₁m₂ = - 1, m₁ तथा m₂ के मान रखने पर
2 × \(\left(\frac{-1}{2}\right)\) = - 1 ⇒ 1 = − 1
अतः दोनों रेखायें लम्बवत् हैं।

प्रश्न 5.
रेखाओं 2x + y = 5 एवं x 2y = 0 के प्रतिच्छेद बिन्दु से गुजरने वाली एवं x- अक्ष से 45° का कोण बनाने वाली की समीकरण लिखिये ।
हल:
रेखाओं 2x + y 5 = (0) और x - 2y = (0) के प्रतिच्छेद बिन्दु से गुजरने वाली रेखा की समीकरण
2x + y - 5 + λ (x - 2y) = 0 ................ (1)
(2 + λ) x + (1 - 2λ) y - 5 = 0

समीकरण (1) से
⇒ 2x + y 5 + 3 (x - 2y ) = 0
⇒ 2x + y - 5 + 3x - 6y = 0
5x - 5y - 5 = 0
∴ x - y = 1

निबन्धात्मक प्रश्न-

प्रश्न 1.
उस सरल रेखा का समीकरण ज्ञात कीजिये जो बिन्दु (3, 4) से जाती है तथा उसके द्वारा अक्षों से काटे गये अंतः खण्डों की लम्बाइयों का योग 14 है।
हल:
माना अंत: खण्ड रूप में रेखा का समीकरण
\(\frac{x}{a}+\frac{y}{b}\) = 1
a एवं b क्रमश: x एवं y अक्ष पर अंतः खण्ड हैं।
∵ यह रेखा बिन्दु (3, 4) से होकर जाती है अतः यह बिन्दु रेख को संतुष्ट करेगा।
⇒ \(\frac{3}{a}+\frac{4}{b}\) = 1
⇒ 3b + 4a = 4b .................. (1)
तथा प्रश्नानुसार
a + b = 14 ..................... (2)
समीकरण (2) से b का मान समीकरण (1) में रखने पर
3 (14 – a) + 4a - a (14 – a) = 0
42 - 3a + 4a - 14a + a2 = 0
a² - 13a + 42 = 0
a² - 7a - 6a + 42 = 0
a (a - 7 ) - 6 (a - 7 ) = 0
(a - 6 ) (a - 7 ) = 0
जब a = 6, एवं a = 7
जब a = 6 तो b = 14 - 6 = 8
अतः अभीष्ट रेखा का समीकरण
\(\frac{x}{6}+\frac{y}{8}\) = 1 या \(\frac{x}{7}+\frac{y}{7}\) = 1
या 4x + 3y = 24 या x + y = 7

प्रश्न 2.
उस सरल रेखा का समीकरण ज्ञात रेखाओं 3x - 4y = 25 तथा 3x + 5y = 17 पर डाले गये लम्ब के पादों पर मिलती है।
हल:
दी गई रेखाओं के समीकरण
तथा
3x - 4y = 25 ....... (1)
3x + 5y = 17 .......... (2)
मूल बिन्दु से जाने वाली और रेखाओं (1) तथा (2) के लम्बवत् रेखाओं की समीकरण क्रमशः होगी-
तथा
—
4x + 3y = 0 ................ (3)
5x - 3y = 0 ................. (4)
अब रेखा (1) एवं रेखा (3) का प्रतिच्छेद बिन्दु (3, - 4) एवं रेखा (2) व रेखा (4) का प्रतिच्छेद बिन्दु \(\left(\frac{3}{2}, \frac{5}{2}\right)\) प्राप्त होता है। प्रश्नानुसार बिन्दु (3, - 4) एवं \(\left(\frac{3}{2}, \frac{5}{2}\right)\) समीकरण ज्ञात करनी है।
∴ अभीष्ट रेखा की समीकरण

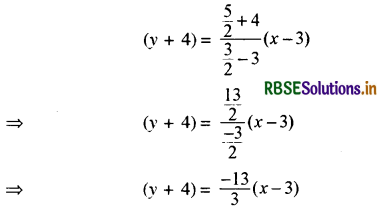
⇒ 3y + 12 = - 13x + 39
⇒ 13x + 3y - 27 = 0
⇒ 13x + 3y = 27

प्रश्न 3.
सिद्ध कीजिए कि बिन्दु (a cost θ, a sin 2θ) से गुजरने वाली तथा सरल रेखा x sec θ + y cosec θ = a पर लम्ब सरल रेखा का समीकरण x cos θ - y sin θ = a cos 2θ है।
हल:
प्रश्नानुसार दी गई सरल रेखा
x sec θ + y cosec θ = a पर लम्ब रेखा का कोई समीकरण x cosec θ - y sec θ k होगा (जहाँ k स्वेच्छ है) .......... (1)
अब यदि रेखा (1) बिन्दु (a cos³θ, a sin³θ) से गुजरती है तो x = a cos³θ, y = a sin³θ समीकरण (1) को सन्तुष्ट करेगा अतः a cos³θ × cosec θ - a sin³θ sec θ = k

प्रश्न 4.
उस सरल रेखा का समीकरण ज्ञात कीजिये जो कि बिन्दु (-5, 1) से होकर जाती है और यह बिन्दु उसके अक्षों के मध्य के अंतः खण्ड को 1 : 3 के अनुपात में विभाजित करती है।
हल:

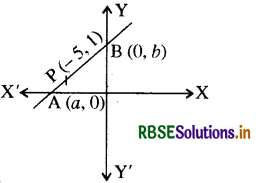
माना कि अक्षों से क्रमशः a एवं b अंतःखण्ड काटने वाली रेखा का समीकरण है-
\(\frac{x}{a}+\frac{y}{b}\) = 1 ................. (1)
यह रेखा अक्षों को क्रमश: A एवं B बिन्दु पर काटती है।
जिनके निर्देशांक (a, 0) और (0, b) हैं।
AB के मध्य की दूरी को 1 : 3 में अंतःखण्ड विभाजित करने वाले बिन्दु P के निर्देशांक (x₁, y₁) हों तो

⇒ 3x + 5y = 20
⇒ 3x - 5y = - 20
⇒ 3x - 5y + 20 = 0

प्रश्न 5.
बिन्दु (0, a) से गुजरने वाली उन सरल रेखाओं के समीकरण ज्ञात कीजिये जिन पर बिन्दु (20, 2a) से डाले गये लम्बों की लम्बाई a है ।
हल:
माना बिन्दु (0, a) से गुजरने वाली रेखा की प्रवणता m है, तो रेखा का समीकरण
(y - a) = mx
⇒ mx - y + a = 0 ....... (1)
प्रश्नानुसार इस रेखा पर (2a, 2a) से डाले गये लम्ब की लम्बाई = a

दोनों पक्षों का वर्ग करने पर
(2m - 1)² = m² + 1
⇒ 4m² - 4m + 1 = m² + 1
⇒ 3m² - 4m = 0
⇒ m (3m - 4) = 0
⇒ m = 0, m = \(\frac{4}{3}\)
(i) जब m = 0 हो तो रेखा का अभीष्ट समीकरण y - a = 0
[समीकरण (1) से]

(ii) जब m = \(\frac{4}{3}\) तो अभीष्ट रेखा की समीकरण
\(\frac{4 x}{3}\) - y + a = 0
⇒ 4x - 3y + 3a = 0

प्रश्न 6.
सरल रेखा 3x + y + 4 = 0 की बिन्दु (1, 2) से दूरी ज्ञात कीजिये जबकि यह दूरी 3x - 4y + 8 = 0 के समान्तर नापी जाये।
हल:
दी गयी रेखाओं के समीकरण
3x + y + 4 = 0 ............. (1)
एवं 3x - 4y + 8 = 0 .............. (2)

प्रश्नानुसार सरल रेखा (1) की बिन्दु (1, 2) से रेखा (2) के समान्तर दूरी ज्ञात करनी है। अब रेखा (1, 2) रेखा (2) के समान्तर रेखा की समीकरण
3x - 4y + k = 0
यह रेखा बिन्दु (1, 2) से गुजरती है अतः निर्देशांकों को सन्तुष्ट कराने पर
⇒ 3 × 1 - 4 × 2 + k = 0
⇒ 3 - 8 + k = 0
∴ k = 5
k का मान रखने पर 3x - 4y + 5 = 0 ..................... (3)
यह वह रेखा है जो कि रेखा (2) के समान्तर है और बिन्दु (1, 2) से गुजरती है। अब रेखा (1) एवं रेखा (3) को हल करने पर

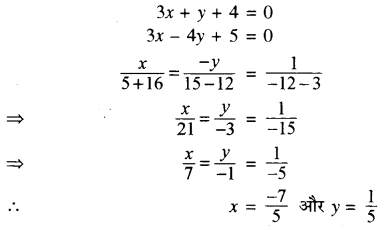
अतः रेखा (1) एवं रेखा (3) को हल करने पर प्रतिच्छेद बिन्दु B\(\left(\frac{-7}{5}, \frac{1}{5}\right)\) प्राप्त होता है।
अत: अभीष्ट दूरी = AB = बिन्दु (1, 2) एवं \(\left(\frac{-7}{5}, \frac{1}{5}\right)\) के मध्य की दूरी

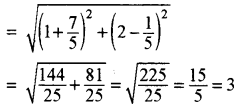
अतः अभीष्ट दूरी = 3 इकाई

प्रश्न 7.
बिन्दु (2, 3) का रेखा x - 2y + 1 = 0 के सापेक्ष प्रतिबिम ज्ञात कीजिये।
हल:
दी गयी रेखा AB (माना ) उसका समीकरण
x - 2y + 1 = 0 .......... (1)
यदि बिन्दु P (2, 3) का x - 2 y + 1 = 0 के सापेक्ष प्रतिबिम्ब Q(h, k) हो, तो रेखा PQ ⊥ AB एवं रेखा PQ का मध्य बिन्दु रेखा AB पर स्थित होगा।

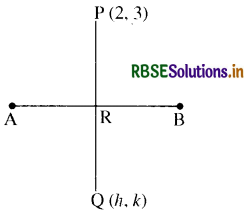
अब रेखा AB के लम्बवत् रेखा का समीकरण
2x + y + k = 0
∵ यह रेखा बिन्दु P(2, 3) से गुजरती है । अत: बिन्दु रेखा के समीकरण को सन्तुष्ट करेगा, अतः
4 + 3 + k ⇒ k = - 7
अत: PQ रेखा का समीकरण
2x + y - 7 = 0 .................. (2)
समीकरण (1) तथा (2) को हल करने पर प्रतिच्छेद बिन्दु R के निर्देशांक

प्रश्न 8.
उस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओं x + 2y + 3 = 0 और 3x + 4y + 7 = 0 के प्रतिच्छेद बिन्दु से होकर जाती हैं एवं अक्षों पर बराबर अन्तः खण्ड काटती हैं।
हल:
दी गई रेखाओं के प्रतिच्छेद बिन्दु निकालने पर-
x + 2y + 3 = 0
3x + 4y + 7 = 0

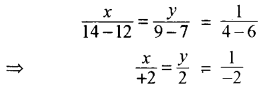
अतः प्रतिच्छेद बिन्दु के निर्देशांक (- 1 - 1) हैं।
अन्तःखण्ड रूप में सरल रेखा का समीकरण होता है।
\(\frac{x}{a}+\frac{y}{b}\) = 1
प्रश्नानुसार अक्षों पर अन्त: खण्ड बराबर है-
अतः b = a
∴ रेखा \(\frac{x}{a}+\frac{y}{a}\) = 1
⇒ x + y = a ......... (1)
रेखा (1) प्रतिच्छेद बिन्दु (- 1, - 1) से गुजरती है, अत: सन्तुष्ट कराने पर
- 1 + (- 1) = a
⇒ a = - 2
a का मान समीकरण (1) में रखने पर अभीष्ट समीकरण है.
x + y = - 2
x + y + 2 = 0

प्रश्न 9.
उस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (3, 5) को दो रेखाओं 4x + y = 1 और 7x - 3y - 35 = 0 के प्रतिच्छेद बिन्दु से मिलाये | सिद्ध कीजिए कि यह रेखा मूल बिन्दु और बिन्दु (8, 34 ) से बराबर दूरी पर है।
हल:
रेखाओं 4x + y - 1 = 0
तथा 7x - 3y - 35 = 0
के प्रतिच्छेद बिन्दु से होकर जाने वाली रेखा का समीकरण होगा
(4x + y 1) + λ (7x - 3y - 35) = 0
⇒ 4x + y - 1 + 7λx - 3λy - 35λ = 0
⇒ x(4 + 7λ) + y(1 - 3λ) (4 + 7λ) - 1 - 3λ = 0
(4 + 7λ)x + (1 - 3λ)y - 1 - 35λ = 0 ................. (1)
यह रेखा (3, 5) से गुजरती है। अत: (3, 5) को सन्तुष्ट कराने पर -
(4 + 7λ) × 3 + (1 - 3λ) × 5 - 1 - 35λ = 0
⇒ 12 + 21λ + 5 ...... 15λ - 1 - 35λ = 0
⇒ - 29λ + 16 = 0
⇒ λ = \(\frac{16}{29}\)
λ का यह मान समी. (1) में रखने पर -

अतः P₁ = P₂
⇒ रेखा (2) की (0, 0) से दूरी = रेखा (2) की (8, 34) से दूरी (इति सिद्धम्)

प्रश्न 10.
उन सरल रेखाओं के समीकरण ज्ञात कीजिए जो रेखाओं y - 3x + 5 = 0 और y - 2x + 2 = 0 के प्रतिच्छेद बिन्दु से गुजरती हैं तथा मूल बिन्दु से 7/√2 इकाई दूरी पर हैं।
हल:
सरल रेखाओं
y - 3x + 5 = 0
तथा y - 2x + 2 = 0 के प्रतिच्छेद बिन्दु से गुजरने वाली रेखा का समीकरण
(y - 3x + 5) + λ (y - 2x + 2) = 0
⇒ y (1 + λ) - x (3 + 2λ) + 5 + 2λ = 0 ............ (1)
रेखा (1) पर (0, 0) से डाले गये लम्ब की लम्बाई

⇒ 2 (25 + 4λ² + 20λ) = 49 (5λ² + 14λ + 10)⇒ 2(25 + 4
⇒ 50 + 8λ² + 40λ = 245λ² + 686λ + 490
⇒ 245λ² - 8λ² + 686λ - 40λ + 490 - 50 = 0
⇒ 237λ² + 646λ + 440 = 0
⇒ 237λ² + 316λ + 330λ + 440 = 0
⇒ 79λ (3λ + 4) + 110 (3λ + 4) = 0)
⇒ (79λ + 110) (3λ + 4) = 0

⇒ x + y = 7 ............... (3)
⇒ अतः रेखायें (2) व (3) अभीष्ट समीकरण हैं ।

प्रश्न 11.
सिद्ध कीजिये कि रेखा 7x + 4y = 3 के किसी भी बिन्दु से दो रेखाओं 3x - 4y = 2 तथा 5x - 12y = 4 पर डाले गये लम्ब परस्पर बराबर हैं।
हल:
माना (x₁, y₁) रेखा 7x + 4y = 3 पर स्थित कोई बिन्दु है।
अतः 7x₁ + 4y₁ = 3
या 7x₁ + 4y₁ - 3 = 0 ....... (1)
बिन्दु (x₁, y₁) से रेखा 3x - 4y = 2 पर डाले गये लम्ब की लम्बाई माना P है।

39x₁ - 52у₁ - 26 = 25x₁ - 60у₁ - 20
या 14x1₁ + 8y₁ - 6 = 0
या 7x₁ + 4y₁ - 3 = 0
यह वही सम्बन्ध है जो (1) में है अतः यह सत्य है|
∴ रेखा 7x + 4y = 3 पर स्थित किसी बिन्दु से रेखाओं 3x - 4y = 2 तथा 5x - 12y = 4 पर डाले गये लम्ब परस्पर बराबर हैं।

बहुचयनात्मक प्रश्न-

प्रश्न 1.
y-अक्ष की प्रवणता है-
(A) 1
(B) 0
(C) ∞
(D) π/2
हल:
(C) ∞

प्रश्न 2.
समीकरण x × \(\frac{1}{2}\) + y × \(\frac{\sqrt{3}}{2}\) = 5 द्वारा निरूपित सरल रेखा निम्न रूप में है-
(A) सममित रूप
(B) झुकाव रूप
(C) अंत:खण्ड रूप
(D) लम्ब रूप
हल:
(D) लम्ब रूप

प्रश्न 3.
रेखा 3x - 4y - 4 = 0 द्वारा x - अक्ष तथा y-अक्ष पर काटे गये अंतः खण्डों की लम्बाई है-
(A) \(\frac{4}{3}\) और - 1
(B) \(\frac{4}{3}\) और 1
(C) \(\frac{4}{3}\) और - 1
(D) \(\frac{4}{3}\) और 1
हल:
(A) \(\frac{4}{3}\) और - 1

प्रश्न 4.
बिन्दु (1, 0) तथा ( -2, √3) को मिलाने वाली रेखा x-अक्ष के साथ 6 कोण बनाती है तो tan 8 का मान है-
(A) √3
(B) - √3
(C) \(\frac{1}{\sqrt{3}}\)
(D) \(\frac{1}{-\sqrt{3}}\)
हल:
(D) \(\frac{1}{-\sqrt{3}}\)

प्रश्न 5.
रेखा के समीकरण 2x + √3y - 4 = 0 को झुकाव रूप में बदलने पर झुकाव रूप में प्रयुक्त अचर राशि के मान हैं-
(A) m = 2, c = 4
(B) m = \(\frac{2}{\sqrt{3}}\), c = - \(\frac{4}{\sqrt{3}}\)
(C) m = \(\frac{\sqrt{3}}{2}\), c = 2
(D) m = \(\frac{-2}{\sqrt{3}}\), c = \(\frac{4}{\sqrt{3}}\)
हल:
(D) m = \(\frac{-2}{\sqrt{3}}\), c = \(\frac{4}{\sqrt{3}}\)

प्रश्न 6.
मूल बिन्दु एवं बिन्दु (a cos θ, a sin θ) से गुजरने वाली रेखा का समीकरण है-
(A) y = x cos θ
(B) y = x tan θ
(C) y = x sin θ
(D) y = x cot θ
हल:
(B) y = x tan θ

प्रश्न 7.
सरल रेखाओं x + y - 5 = 0 और y + 2x - 1 = 0 का प्रतिच्छेद बिन्दु है-
(A) (4, 1)
(B) (1, 1)
(C) (- 4, 9)
(D) (6, 1)
हल:
(C) (- 4, 9)

प्रश्न 8.
सरल रेखाओं 3x - 4y = 7 के समान्तर और मूल बिन्दु से गुजरने वाली रेखा का समीकरण है-
(A) 3x - 4y = 1
(B) 3x - 4y = 0
(C) 4x - 3y = 1
(D) 3y - 4x = 0
हल:
(B) 3x - 4y = 0

प्रश्न 9.
मूल बिन्दु से सरल रेखा x + √3y = 1 पर डाले गये लम्ब की लम्बाई p है तो P का मान है-
(A) \(\frac{1}{4}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{\sqrt{3}}{2}\)
(D) 1
हल:
(B) \(\frac{1}{2}\)

प्रश्न 10.
यदि रेखाएँ y = mx + 5 तथा 3x + 5y तो m का मान है-
(A) \(\frac{5}{3}\)
(B) - \(\frac{5}{3}\)
(c) - \(\frac{3}{5}\)
(D) \(\frac{3}{5}\)
हल:
(A) \(\frac{5}{3}\)

प्रश्न 11.
सरल रेखा 3x - 4y + 7 = 0 पर लम्ब और बिन्दु (1, - 2) में से गुजरने वाली रेखा का समीकरण होगा-
(A) 4x + 3y – 2 = 0
(B) 4x + 3y + 2 = 0
(C) 4x - 3y + 2 = 0
(D) 4x - 3y - 2 = 0
हल:
(B) 4x + 3y + 2 = 0

प्रश्न 12.
सरल रेखाओं 4x - 3y + 8 = 0 और 3y - 4x - 6 = 0 के मध्य की दूरी है-
(A) 14
(B) 2
(C) \(\frac{14}{5}\)
(D) \(\frac{2}{5}\)
हल:
(D) \(\frac{2}{5}\)

प्रश्न 13.
रेखाओं 3y + x - 10 = 0 तथा 2x - 5y + 13 = 0 पर स्थित बिन्दु हैं- हैं-
(A) (0, 0)
(B) (6, 5)
(C) (4, 2)
(D) (1, 3)
हल:
(D) (1, 3)

प्रश्न 14.
यदि y = mx + c और x = my + c परस्पर लम्बवत् हैं तो m का मान ज्ञात कीजिये-
(A) 1
(B) 1
(C) 0
(D) नहीं ज्ञात कर सकते हैं
हल:
(B) 1

प्रश्न 15.
(1, - 1) से गुजरने वाली व 2x - 3y = 5 के समान्तर रेखा का समीकरण है-
(A) 2x + 3y = - 1
(B) 3x + 2y = 1
(C) 2x - 3y = 5
(D) 2x - 3y = 1
हल:
(C) 2x - 3y = 5

प्रश्न 16.
x = 3, y = 4 व 4x - 3y + a = 0 रेखायें संगामी हैं तो a का मान होगा-
(A) 12
(B) - 12
(C) 0
(D) - 7
हल:
(C) 0

प्रश्न 17.
सरल रेखा 3x - 4y = 7 के समान्तर और मूल बिन्दु से जाने वाली रेखा का समीकरण है-
(A) 3x - 4y = 1
(B) 3x - 4y = 0
(C) 4x - 3y = 1
(D) 3y - 4x = 0
हल:
(B) 3x - 4y = 0

प्रश्न 18.
सरल रेखाओं 4x - y - 7 = 0 और 5x + y - 11 = 0 के प्रतिच्छेद बिन्दु को मूल बिन्दु से मिलाने वाली रेखा की प्रवणता है-
(A) - 2
(B) 2
(C) \(\frac{1}{2}\)
(D) \(\frac{- 1}{2}\)
हल:
(C) \(\frac{1}{2}\)

प्रश्न 19.
रेखा y = mx + 10 रेखा 2x + 3y = 9 पर लम्ब है तो m बराबर है-
(A) \(\frac{3}{2} \)
(B) \(\frac{2}{3}\)
(C) \(\frac{-3}{2}\)
(D) \(\frac{-2}{3}\)
हल:
(A) \(\frac{3}{2}\)

प्रश्न 20.
सरल रेखा x sec θ + y cosec θ = a पर मूल बिन्दु से डाले गये लम्ब की लम्बाई है-
(A) a sin θ cos θ
(B) a cos θ cosec θ
(C) a cosec θ sec θ
(D) a
हल:
(A) a sin θ cos θ

प्रश्न 21.
यदि रेखायें a₁x - b₁y + c₁ = 0 एक-दूसरे के लम्बवत् हों
(A) a₁b₂ + a₂b₁ = 0
(B) a₁a₂ + b₁b₂ = 0
(C) a₁b₂ - a₂b₁ = 0
(D) a₁a₂ - b₁b₂ = 0
हल:
(D) a₁a₂ - b₁b₂ = 0

प्रश्न 22.
बिन्दु (3, 8) का रेखा x + 2y - 7 = 0 में प्रतिबिम्ब है-
(A) (- 1, - 4)
(B) (- 3, - 8)
(C) (1, - 4)
(D) (3, 8)
हल:
(B) (- 3, - 8)

प्रश्न 23.
बिन्दु (a, b) से गुजरने वाली तथा \(\frac{x}{a}+\frac{y}{b}\) = 1 के समान्तर रेखा का समीकरण है-
(A) \(\frac{x}{a}+\frac{y}{b}\) = 5
(B) \(\frac{x}{a}+\frac{y}{b}\) = 2
(C) \(\frac{x}{a}+\frac{y}{b}\) = 0
(D) \(\frac{x}{a}+\frac{y}{b}\) - 5 = 0
हल:
(B) \(\frac{x}{a}+\frac{y}{b}\) = 2

प्रश्न 24.
यदि (4, 3) तथा (2, k) से गुजरने लम्बवत् हो तो k बराबर है- वाली रेखा y = 2x + 3 के
(A) 2
(B) 3
(C) 4
(D) 5
हल:
(C) 4

प्रश्न 25.
रेखाओं ax + 2by + 3b = 0 तथा bx - 2ay - 3a = 0 के प्रतिच्छेद बिन्दु से जाने वाली तथा x-अक्ष के समान्तर रेखा जबकि (a, b ≠ 10, 0) निम्नवत् है-
(A) x-अक्ष के ऊपर तथा उससे \(\frac{3}{2}\) इकाई दूरी पर स्थित
(B) x- अक्ष के ऊपर तथा उससे \(\frac{3}{2}\) इकाई दूरी पर स्थित
(C) x-अक्ष के नीचे तथा इससे \(\frac{3}{2}\) इकाई दूरी पर स्थित
(D) x-अक्ष के नीचे तथा उससे \(\frac{3}{2}\) दूरी पर
हल:
(C) x-अक्ष के नीचे तथा इससे \(\frac{3}{2}\) इकाई दूरी पर स्थित

रिक्त स्थानों की पूर्ति करो-

प्रश्न 1.
बीजगणित एवं ज्यामिति के संयोजन को ................................. ज्यामिति कहते हैं।
हल:
निर्देशांक

प्रश्न 2.
रेखा l, x- अक्ष की धनात्मक दिशा के साथ जो कोण बनाती है, उसे रेखा l का ......................... कहते हैं।
हल:
झुकाव

प्रश्न 3.
यदि θ किसी रेखा l का झुकाव है, तो tan θ को रेखा l की ......................... कहते हैं।
हल:
ढाल

प्रश्न 4.
x-अक्ष की ढाल ............................. है।
हल:
शून्य

प्रश्न 5.
यदि रेखाएँ l₁ व l₂ समान्तर हैं तब उनके झुकाव .................................... है।
हल:
समान

प्रश्न 6.
दो ऊर्ध्वेतर रेखाएँ l₁ तथा l₂ परस्पर लम्ब होती हैं यदि और केवल यदि उनकी ढाल परस्पर ............................... है।
हल:
ऋणात्मक व्युत्क्रम

प्रश्न 7.
यदि एक रेखा x - अंतखण्ड a और y - अंतखण्ड b बनाती है तब रेखा का समीकरण ............................... होगा।
हल:
\(\frac{x}{a}+\frac{y}{b}\) = 1

प्रश्न 8.
मूल बिन्दु से लाम्बिक दूरी Φ और इस लम्ब तथा धन x-अक्ष के बीच ω कोण बनाने वाली रेखा का समीकरण .............................. है।
हल:
x cos ω + y sin ω = p

प्रश्न 9.
समान्तर रेखाओं Ax + By + C₁ = 0 तथा Ax + By + C₁ = 0 के बीच की दूरी .............................. है।
हल:
\(\frac{\left|c_1-c_2\right|}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}\)

प्रश्न 10.
x - अक्ष का समीकरण ....................................... होता है।
हल:
y = 0

निम्नलिखित कथनों के लिए सत्य/असत्य लिखिए-

प्रश्न 1.
दो रेखाएँ लम्ब होती हैं यदि और केवल यदि ढालों का गुणनफल - 1 है।
हल:
सत्य

प्रश्न 2.
तीन बिन्दु A, B और C संरेख होते हैं यदि और केवल यदि AB की ढाल = BC की ढाल
हल:
सत्य

प्रश्न 3.
x - अक्ष से a दूरी पर स्थित क्षैतिज रेखा का समीकरण या तो x = a या x = -a है|
हल:
असत्य

प्रश्न 4.
y- अक्ष से b दूरी पर स्थित ऊर्ध्वाधर रेखा का समीकरण या तो x = b या x = - b है।
हल:
सत्य

प्रश्न 5.
बिन्दु (x₁, y₁) से जाने वाली व m. ढाल वाली रेखा का समीकरण (x₁ - x) = m(y₁ - y)
हल:
असत्य

प्रश्न 6.
बिन्दुओं (x₁, y₁) तथा (x₂, y₂) से जाने वाली रेखा का समीकरण
y - y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x - x₁)
हल:
सत्य

प्रश्न 7.
सरल रेखा का समीकरण, जो बिन्दु (x₁, y₁) से जाती है तथा x- अक्ष की धनात्मक दिशा से 8 कोण बनाती है, होगा-
\(\frac{x-x_1}{\sin \theta}=\frac{y-y_1}{\cos \theta}\) = r, जहाँ r (x₁, y₁) तथा (x, y) के बीच की दूरी है।
हल:
असत्य

प्रश्न 8.
रेखा का समीकरण जो बिन्दु (x, y, ) से जाती है तथा रेखा y = mx + c के साथ x कोण बनाती है, होगा-
y - y₁ = \(\frac{m \pm \tan \alpha}{1 \pm m \tan \alpha}\) (x - x₁)
हल:
सत्य

प्रश्न 9.
बिन्दु (x₁, y₁) से रेखा ax + by + c = 0 की दूरी
d = \(\frac{a x_1+b y_1+c}{\sqrt{a^2+b^2}}\) है|
हल:
सत्य

प्रश्न 10.
रेखा ax + by + c = 0 के लम्बवत् रेखा bx + ay + λ = 0 होगी, जहाँ λ स्थिरांक है।
हल:
असत्य

सही मिलान कीजिए-

भाग (A)	भांग (B)
1. रेखा 2x - y + 3 = 0 एवं x + 2y + 3 = 0 के मध्य कोण	(a) (4, 7)
2. बिन्दु ( 4, -13 ) का रेखा 5x + y + 6 = 0 का प्रतिबिम्ब	(b) - \(\frac{7}{2}\)
3. रेखाओं 4x + 3y - 10 = 0, 5x - 12y + 26 = 0 और 7x + 24y – 50 = 0 के समान दूरी पर स्थित बिन्दु	(c) 3x + y – 20 = 0
4. किसी त्रिभुज का केन्द्रक (2, 7) हो तथा दो शीर्ष ( 4, 8) व (-2, 6) होने पर तीसरा शीर्ष	(d) 90°
5. बिन्दु (2, 5) व (x, 3) से जाने वाली (e) y = -5 रेखा का ढाल 2 है तो x का मान	(e) y = - 5
6. बिन्दु (3, - 5) व (1, 2) से जाने वाली रेखा का ढाल	(f) x = 2
7. रेखा का समीकरण जो x-अक्ष के समान्तर हो तथा बिन्दु (3, 5) से गुजरे	(g) (- 1, - 14)
8. रेखाओं x = - 2 और x = 6 से बराबर दूरी पर स्थित रेखा का समीकरण	(h) y = 2x + 3
9. रेखा का समीकरण जिसका ढाल 2 और y - अन्त: खण्ड 3 हो	(i) (0,0)
10. रेखा का समीकरण जो बिन्दु (6, 2) से गुजरती है तथा जिसकी ढाल -3 है	(j) 1

उत्तरमाला
1. (d)
2. (g)
3. (i)
4. (a)
5. (j)
6. (b)
7. (e)
8. (f)
9. (h)
10. (c)