RBSE Class 11 Maths Important Questions Chapter 1 समुच्चय

Rajasthan Board RBSE Class 11 Maths Important Questions Chapter 1 समुच्चय Important Questions and Answers.

RBSE Class 11 Maths Chapter 1 Important Questions समुच्चय

अतिलघूतरात्मक प्रश्न- 

प्रश्न 1.
यदि U = {a, e, i, o, u} तथा A' = {e, i, u} है, तो A को सारणीबद्ध रूप में लिखिए।
हल:
A = {a, o}

प्रश्न 2.
यदि P = { 1, 3, 5, 7, 9} तथा P = {2, 4, 6, 8} है, तो इनका सार्वत्रिक समुच्चय लिखिए ।
हल:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}

प्रश्न 3.
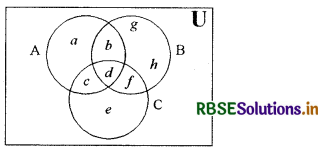
दिए गए वेन आरेख को देखकर (A ∩ B) ∪ C का मान लिखिए।
हल:
{b, c, d, e, f}

प्रश्न 4.
यदि n(P) = 20, n(Q) = 12 तथा n(P ∩ Q) = 4 हो, तो n (P - Q) का मान लिखिए।
हल:
n(P - Q) = n(P) - n(P ∩ Q)
= 20 - 4 = 16

प्रश्न 5.
यदि A तथा B में क्रमशः 4 तथा 7 अवयव हैं तो A ∪ B में न्यूनतम अवयवों की संख्या बताइए।
हल:
यहाँ n(A) = 4 और n (B) = 7
अब A ∪ B में अवयवों की संख्या न्यूनतम होगी, यदि A ⊆ B,
तब A ∪ B = B
तब A ∪ B में न्यूनतम अवयवों की संख्या = n(B) = 7

प्रश्न 6.
दो समुच्चयों के संघ का क्रम विनिमेय नियम लिखिए।
हल:
समुच्चय के संघ का क्रम विनिमेय नियम
A ∪ B = B ∪ A

प्रश्न 7.
कोई ऐसे दो सार्वत्रिक समुच्चय ∪ लिखिए जिसके समुच्चय A = {a, b, d}, B = {x/x Udaipur शब्द के अक्षर हैं} तथा C = {a, i, u} उपसमुच्चय हैं|
हल:
U = {a, b, d, i, u, p, r} तथा
U = {x x अंग्रेजी वर्णमाला का अक्षर }

प्रश्न 8.
'द मार्गन नियम' लिखिए ।
हल:
(i) (A ∪ B)'= A' ∩ B'
(ii) (A ∩ B)'= A' ∪ B'

प्रश्न 9.
दिए गए वेन आरेख से A - B लिखिए ।
हल:
A - B = {1, 2, 3, 4} - {1, 3, 5, 7}
= {2, 4}

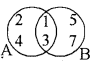
प्रश्न 10.
‘MORADABAD' शब्द में स्वरों का समुच्चय लिखिए ।
हल:
{A, O}

प्रश्न 11.
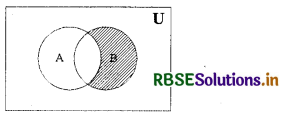
B - A को वेन आरेख से प्रदर्शित कीजिए ।
हल:

प्रश्न 12.
समुच्चय निर्माण विधि का प्रयोग करके निम्न को प्रदर्शित करें-
A = \(\left\{1, \frac{1}{4}, \frac{1}{9}, \frac{1}{16}, \frac{1}{25}, \ldots .\right\}\)
हल:
A = {\(\frac{1}{n^2}\), n ∈ N}

प्रश्न 13.
समुच्चय निर्माण विधि का प्रयोग करके निम्न को प्रदर्शित करें-
B = {1, 5, 10, 15, .....}
हल:
B = {x:x एक प्राकृत संख्या है जो 5 का गुणज है और x > 1}

प्रश्न 14.
किन्हीं तीन समुच्चयों A, B और C के लिए साहचर्य नियम लिखिए ।
हल:
(i) A ∪ (B ∪ C) = (A ∪ B) ∪ C
(ii) A ∩ (B ∩ C) = (A ∩ B) ∩ C

प्रश्न 15.
किन्हीं तीन समुच्चयों A, B और C के लिए वितरण नियम लिखिए ।
हल:
(i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

प्रश्न 16.
परीक्षण कीजिए कि क्या निम्न कथन सत्य है या असत्य है ?
(i) Φ ∈ Φ
(ii) 0 ∈ Φ
(iii) Φ = {0}
हल:
(i) असत्य, क्योंकि Φ में कोई अवयव नहीं होता है ।
(ii) असत्य, क्योंकि Φ में कोई अवयव नहीं होता है ।
(iii) असत्य, चूँकि इसमें कोई अवयव नहीं होता है।

लघूत्तरात्मक प्रश्न-

प्रश्न 1.
निम्नलिखित में से कौन-कौनसे संग्रह एक समुच्चय निरूपित नहीं करते हैं? कारण सहित बताइए ।
(a) A = {x : x कक्षा XI का लम्बा छात्र है}
(b) B = {x:x कक्षा XII का छात्र है जिसकी लम्बाई 5 फुट से अधिक है}
(c) C = {x : x क्रिकेट का अच्छा खिलाड़ी है}
(d) D = {xx क्रिकेट का खिलाड़ी है, जिसने टेस्ट क्रिकेट में पाँच हजार से अधिक रन बनाए हैं}
हल:
(a) A {x : x कक्षा XI का लम्बा छात्र है }
∵ लम्बा होने का कोई स्पष्ट संकेत नहीं है जिसके आधार पर यह बताया जा सके कि कोई छात्र संग्रह A में सम्मिलित होगा या नहीं। अतः A एक संग्रह निरूपित करता है समुच्चय नहीं।

(b) B = {x : x कक्षा XII का छात्र है जिसकी लम्बाई 5 फुट से अधिक है }
यहाँ हम किसी भी छात्र की लम्बाई नापकर हम स्पष्ट रूप से बता सकते हैं कि वह समूह B में सम्मिलित होगा या नहीं, अर्थात् यहाँ B छात्रों का सुपरिभाषित समूह है, अतः B एक समुच्चय निरूपित करता है।

(c) C = {x : x क्रिकेट का अच्छा खिलाड़ी है}
क्रिकेट का अच्छा खिलाड़ी होने की कोई स्पष्ट परिभाषा नहीं है, अत: संग्रह C एक समुच्चय को निरूपित नहीं करता है.|

(d) D {x:x क्रिकेट का खिलाड़ी है, जिसने टेस्ट क्रिकेट में पाँच हजार से अधिक रन बनाए हैं}
यहाँ किसी खिलाड़ी द्वारा बनाए गए रनों के ज्ञात होने पर स्पष्ट रूप से बताया जा सकता है कि वह समूह D में सम्मिलित होगा या नहीं। अतः D एक समुच्चय निरूपित करता है।

प्रश्न 2.
वास्तविक संख्याओं के निम्नलिखित समुच्चयों को तालिका/ सारणीबद्ध रूप में लिखिए-
(a) (x : x² - 9x + 20 = 0}
(b) {x : x³ + 1 = 0}
(c) {x : x² - 2 = 10}
(d) {x : x अभाज्य संख्या है, x ≤ 11}
हल:
(a) {x : x² - 9x + 20 = 0}
दिया गया समुच्चय समीकरण x² - 9x + 20 = 0 के मूलों का समुच्चय है । अतः
x² - 9x + 20 = 0
⇒ x² - 5x - 4x + 20 = 0
⇒ x (x - 5) - 4 (x - 5 ) = 0
⇒ (x - 5 ) (x - 4 ) = 0
⇒ x = 5, 4
∴ अभीष्ट समुच्चय = {4, 5}

(b) {x : x³ + 1 = 0}
समीकरण x³ + 1 = 0 को हल करने पर
(x + 1) (x² - x + 1) = 0
या x = -1, \(\frac{1 \pm i \sqrt{3}}{2}\)
परन्तु \(\frac{1 \pm i \sqrt{3}}{2}\) वास्तविक संख्याएँ नहीं हैं
∴ अभीष्ट समुच्चय = {- 1}

(c) {x : x² - 2 = 10}
समीकरण x² - 2 = 10 को हल करने पर
या x² = 12
∴ x = √12
या x = ± 2 √3
∴ दिया गया समुच्चय = {2 √3, – 2 √3 }

(d) {x:x अभाज्य संख्या है, x ≤ 11}
11 तक की अभाज्य संख्याएँ क्रमश: 2, 3, 5, 7, 11 होंगी ।
अतः अभीष्ट समुच्चय = {2, 3, 5, 7, 11}

प्रश्न 3.
यदि A = {x : x ∈ N, 1 ≤ x ≤ 3} तथा B = {y : 3y = 9 या 2y = 2 या y - 1 = 1} तो क्या A = B सत्यं है?
हल:
A = { x : x ∈ N, 1 ≤ x ≤ 3}
तथा B = {y : 3y = 9 या 2y = 2 या y - 1 = 1}
अब 1 ≤ x < 3 ⇒ x = 1, 2, 3 [∵ x ∈ N]
∴ A = {1, 2, 3}
पुन: 3y = 9 ⇒ y = 3,
2y = 2 ⇒ y = 1
तथा y - 1 = 1 ⇒ y = 2
∴ B = {3, 1, 2} = {1, 2, 3}
स्पष्ट है कि A और B के अवयव समान हैं । अतः कथन A = B सत्य है।

प्रश्न 4.
यदि A = {1, 2, 6, 9}, B = {2, 4, 6, 8} तथा C = {3, 4, 9} तो A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) को सत्यापित कीजिए ।
हल:
B ∩ C = B और C के उभयनिष्ठ अवयवों का समुच्चय = {4}
∴ A ∪ (B ∩ C) = A व (B ∩ C) के सभी अवयवों का समुच्चय
= {1, 2, 4, 6, 9}
पुनः A ∪ B = A व B के सभी अवयवों का समुच्चय
= {1, 2, 4, 6, 8, 9}
इसी प्रकार A ∪ C = {1, 2, 3, 4, 6, 9}
∴ (A ∪ B) ∩ (A ∪ C) = (A ∪ B) व (A ∪ C)
के उभयनिष्ठ अवयवों का समुच्चय
= {1, 2, 4, 6, 9}
∴ A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) उत्तर

प्रश्न 5.
यदि A = {x : x = 2n, n धन पूर्णांक है} तथा B = {x: x 3n, n धन पूर्णांक है }, तो A ∩ B का मान ज्ञात कीजिए ।
हल:
∵ n धन पूर्णांक है ∴ n = 1, 2, 3, 4, ...................... रखने पर
x = 2n = 2, 4, 6, 8, 10, 12 .........................
तब A = {2, 4, 6, 8, 10, 12 .......................}
तथा x = 3n = 3, 6, 9, 12, 15, 18 .............................
तब B = {3, 6, 9, 12, 15, 18 ......................}
अत: A ∩ B = A और B के उभयनिष्ठ अवयवों का समुच्चय
= {6, 12, 18, 24...............}
= {x : x = 6n, n धन पूर्णांक है}

प्रश्न 6.
यदि A = {1, 2, 3}, B = {2, 3, 4}, तथा C = {3, 4, 5, 6} हो, तो (A ∩ B) - C ज्ञात कीजिए।
हल:
A = {1, 2, 3}, B = {1, 2, 3}, C = {3, 4, 5, 6)
∴ (A ∩ B) = {2, 3, 4} ∩ {2, 3, 4}
= {2, 3}
अब (A ∩ B) - C = {2, 3} - {3, 4, 5, 6}
= {2}

प्रश्न 7.
रिक्त समुच्चय A के लिए सिद्ध कीजिए कि (A)' = A
हल:
यहाँ
A = { }
माना x सार्वत्रिक समुच्चय है, तब
A' = x के उन सभी अवयवों का समुच्चय जो A में नहीं है।
= x (∵ x का कोई अवयव A में नहीं है )
अब (A') = x
= x के उन अवयवों का समुच्चय जो x में नहीं है।
= { } (∵ x का कोई अवयव x में नहीं है )
= A
∴ (A') ' = A

प्रश्न 8.
तर्क द्वारा सिद्ध कीजिए कि समुच्चय A और B के लिए A - B B' - A' सत्य है।
हल:
यहाँ हमें सिद्ध करना होगा कि-
(A - B) ⊆ (B' - A') तथा (B' - A') ⊆ (A - B )
माना x ∈ (A - B) ⇒ x ∈ A तथा x ∉ B
⇒ x ≠ A' तथा x ∉ B'
⇒ x ∈ B' तथा x ∉ A
⇒ x ∈ (B' - A')
∴ (A - B) ⊆ (B′ - A') ................ (i)
पुनः
x ∈ (B' - A') ⇒ x ∈ B' तथा x ∉ A'
⇒ x ≠ B तथा x ∈ A
⇒ x ∈ A तथा x ∉ B
⇒ x ∈ (A - B)
∴ (B′ – A′) ⊆ (A - B) .................. (ii)
समीकरण (i) तथा (ii) से, A - B = B' - A' सत्य है।

प्रश्न 9.
एक कक्षा के वार्षिक समारोह में प्रत्येक छात्र ने संगीत तथा नाटक में से कम से कम एक में भाग लिया। यदि कक्षा में कुल 40 छात्र हों तथा संगीत में भाग लेने वालों की संख्या 20 और नाटक में भाग लेने वालों की संख्या 35 हो, तो ज्ञात कीजिए कि कितने छात्रों ने संगीत तथा नाटक दोनों में भाग लिया?
हल:
माना कि संगीत में भाग लेने वालों का समुच्चय A व नाटक में भाग लेने वालों का समुच्चय B है ।
∴ संगीत तथा नाटक दोनों में भाग लेने वालों की संख्या
= n(A ∩ B)
∵ n(A ∪ B) = n(A) + n (B) - n (A ∩ B)
यहाँ n(A ∪ B) = 40, n (A) = 20, n (B) = 35
∴ n(A ∩ B) = n(A) + n(B) - n(A ∪ B)
= 20 + 35 - 40
= 15

प्रश्न 10.
किसी परीक्षा में गणित अथवा अंग्रेजी में प्रथम श्रेणी अंक प्राप्त करने वाले 80 छात्रों में से 50 छात्रों ने गणित में तथा 10 छात्रों ने अंग्रेजी और गणित में प्रथम श्रेणी में अंक प्राप्त किए। बताइए कि कितने छात्रों ने अंग्रेजी में प्रथम श्रेणी अंक प्राप्त किए?
हल:
माना M = गणित में प्रथम श्रेणी अंक प्राप्त करने वाले छात्रों का समुच्चय
E = अंग्रेजी में प्रथम श्रेणी अंक प्राप्त करने वाले छात्रों का समुच्चय
तब M ∪ E = गणित अथवा अंग्रेजी में प्रथम श्रेणी अंक प्राप्त करने वाले छात्रों का समुच्चय
तथा M ∩ E = गणित और अंग्रेजी में प्रथम श्रेणी अंक प्राप्त
करने वाले छात्रों का समुच्चय
प्रश्नानुसार, n(M) = 50, n (M ∪ E) = 80, n(M ∩ E) = 10
∴ सूत्र n (M ∪ E) = n(M) + n(E) - n (M ∩ E) से
80 = 50 + n(E) - 10
या n (E) = 80 - 50 + 10 = 40
अतः अंग्रेजी में प्रथम श्रेणी अंक प्राप्त करने वाले छात्रों की संख्या
= n(E) = 40

प्रश्न 11.
20 लोगों के एक समूह में 8 लोग चाय पीते हैं, परन्तु कॉफ नहीं पीते हैं और 13 लोग चाय पीते हैं। बताइए कि कितने लोग कॉफी पीते हैं, परन्तु चाय नहीं पीते हैं?
हल:
माना T = चाय पीने वालों का समुच्चय
तथा C = कॉफी पीने वालों का समुच्चय
प्रश्नानुसार n(T) = 13
n(T ∪ C') = चाय या कॉफी पीने वालों का समुच्चय = 20
तथा n(T ∩ C) = चाय पीने वाले परन्तु कॉफी न पीने वालों का समुच्चय = 8
अब ∵ n(T ∩ C') = n(T) - n(T ∩ C) से
8 = 13 - n(T ∩ C)
या n(T ∩ C) = 13 - 8 = 5
पुनःसूत्र n(T ∩ C) = n(T ∪ C) - n(T ∩ C) - n (C ∩ T') से
5 = 20 - 8 - n(C ∩ T)
या n(C ∩ T') = 20 - 8 - 5 = 7
अतः उन लोगों की संख्या जो कॉफी पीते हैं, परन्तु चाय नहीं पीते हैं
= n(C ∩ T') = 7

निबन्धात्मक प्रश्न-

प्रश्न 1.
यदि x = {4ⁿ - 3n - 1 : n ∈ N} और y = {9 (n - 1) :n ∈ N} तो सिद्ध कीजिए कि x ⊂ y
हल:
समुच्चय x के अवयव, (4ⁿ - 3n - 1 ) के वे सभी मान हैं जो
इसमें n = 1, 2, 3, 4, ...................... रखने पर प्राप्त होते हैं। [∵ n ∈ N]
∴ जब n = 1, तो 4ⁿ - 3n - 1 = 4 - 3 - 1 = 0
जब n = 2, तो 4ⁿ - 3n - 1 = 4² - 3(2) - 1 = 16 - 6 - 1 = 9
जब n = 3, तो 4ⁿ - 3n - 1 = 4³ - 3(3) - 1 = 64 - 9 - 1 = 54
जब n = 4, तो 4ⁿ - 3n - 1 = 4⁴ - 3(4) - 1 = 256 - 12 - 1 = 243
............................................................................................................
∴ x = {0, 9, 54, 243 ............................}
पुनः समुच्चय y के अवयव 9 (n - 1 ) के वे सभी मान हैं जो
इसमें n = 1, 2, 3, 4 ........................ रखने पर प्राप्त होते हैं। [∵ n∈ N]
∴ जब n = 1, तो 9 (n - 1) = 9 (1 - 1) = 9 (0) = 0
जब n = 2, तो 9 (n - 1 ) = 9 (2 - 1) = 9 (1) = 9
जब n = 3, तो 9 (n - 1 ) = 9 (3 - 1) = 9 (2) = 18
जब n = 4, तो 9 (n - 1) = 9 (4 - 1) = 9 (3) = 27
..........................................................................
∴ y = {0, 9, 18, 27, 36............................}.
स्पष्ट है कि समुच्चय x के सभी अवयव समुच्चय y में हैं तथा x ≠ y ∴ x ⊂ y

प्रश्न 2.
यदि A = {p, q, r, s}, B = {q, s, u} तथा C = {r, s, t, u} हो, तो निम्न का सत्यापन कीजिए-
(i) (A - B) Ɑ (A - C) = A - (B n C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(iii) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
हल:
(i) A - B = {p, q, r, s} - {q, s, u}
= {p, r}
तथा A - C = {p, q, r, s} - {r, s, t, u}
= {p, q}
∴ (A - B) ∪ (A - C) = {p, r} ∪ {p, q}
= {q, r, p} .................... (i)
तथा B ∩ C = {q, s, u} ∩ {r, s, t, u}
= {s, u}
∴ A - (B ∩ C) = {p, q, r, s} - {s, u}
= {p, q, r} .................... (ii)
अतः समीकरण (i) व (ii) से-
(A - B) ∪ (A - C) = A - (B ∩ C)

(ii) B ∪ C = {q, s, u} ∪ {r, s, t, u}
= {q, r, s, t, u}
A ∩ (B ∪ C) = {p, q, r, s} ∩ {q, r, s, t, u}
= {q, r, s} .......... (i)
A ∩ B = {p, q, r, s} ∩ {q, s, u}
= {q, s}
A ∩ C = {p, q, r, s} ∩ {r, s, t, u}
= {r, s}
∴ (A ∩ B) ∪ (A ∩ C)= {q, s} ∪ {r, s}
= {q, r, s} ................... (ii)
समीकरण (i) व (ii) से-
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

(iii) B ∩ C = {q, s, u} ∩ {r, s, t, u}
= {s, u}
A ∪ (B ∩ C)= {p, q, r, s} ∪ {s, u}
= {p, q, r, s, u} ........ (i)
(A ∪ B) = {p, q, r, s} ∪ {q, s, u}
= {p, q, r, s, u}
A ∪ C = {p, q, r, s} ∪ {r, s, t, u}
= {p, q, r, s, t, u}
∴ (A ∪ B) ∩ (A ∪ C) = {p, q, r, s, u} ∩ {p, q, r, s, t, u}
= {p, q, r, s, u} ............ (ii)
समीकरण (i) व (ii) से-
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

प्रश्न 3.
1,000 व्यक्तियों के समूह में 750 व्यक्ति हिन्दी बोलते हैं और 400 व्यक्ति बंगाली बोलते हैं। कितने व्यक्ति केवल हिन्दी बोल सकते हैं? कितने व्यक्ति केवल बंगाली बोल सकते हैं? कितने व्यक्ति हिन्दी और बंगाली दोनों बोल सकते हैं?
हल:
माना A = {x : x हिंन्दी बोलते हैं}
B = {x : x बंगाली बोलते हैं }
तब A - B = {x : x हिन्दी बोलते हैं और बंगाली नहीं बोल सकते}
B - A = {x : x बंगाली बोलते हैं और हिन्दी नहीं बोल सकते }
A ∩ B = {x : x हिन्दी और बंगाली दोनों बोलते हैं}
दिया है- n(A) = 750, n(B) = 400, n (A ∪ B) = 1,000
सूत्र से- n(A ∩ B) = n(A) + n(B) - n(A ∪ B)
= 750 + 400 - 1,000 = 150
∴ हिन्दी और बंगाली दोनों बोलने वालों की संख्या 150 है।
n(A) = n(A - B ) + n (A ∩ B)
n(A - B) = n(A) - n(A ∩ B )
= 750 - 150 600
n(B - A) = n(B) - n (AB) = 400 - 150 = 250
इस प्रकार, केवल हिन्दी बोलने वालों की संख्या = 600
और केवल अंग्रेजी बोलने वालों की संख्या = 250

प्रश्न 4.
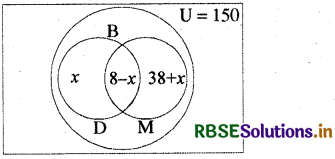
150 व्यक्तियों की किसी कार्यशाला में 58 भारतीय महिलाओं तथा 46 पुरुषों ने भाग लिया। इन भारतीयों में 8 डॉक्टर हैं तथा 48 या तो पुरुष हैं अथवा डॉक्टर हैं । गोष्ठी में कोई विदेशी डॉक्टर नहीं है । बताइए कि कितनी महिला डॉक्टर भाग ले रही हैं ?

हल:
माना सभी व्यक्तियों का समुच्चय U है ।
सभी भारतीयों का समुच्चय = B
सभी पुरुषों का समुच्चय = M
तथा सभी डॉक्टरों का समुच्चय = D
माना कि महिला डॉक्टरों की संख्या = x है ।
अतः शेष महिलाओं की संख्या = 58 - x
शेष पुरुष डॉक्टरों की संख्या = 8 - x
अत: पुरुषों की संख्या = 46 - (8 - x)
= 38 + x

वेन आरेख से -
x + (8 - x) + (38 + x) = 48
x + 8 - x + 38 + x = 48
46 + x = 48
⇒ x = 48 - 46 = 2
अर्थात् महिला डॉक्टरों की संख्या = 2

बहुचयनात्मक प्रश्न-

प्रश्न 1.
समुच्चय {x:x ∈ N, x अभाज्य, 3 < x < 5} है—
(A) {4}
(B) {3, 5}
(C) रिक्त
(D) अरिक्त
हल:
(C) रिक्त

प्रश्न 2.
यदि समुच्चय A = {x : x = 2n, n प्राकृत संख्या} है, तो सत्य है-
(A) 1 ∈ A
(B) 0 ∈ A
(C) 4 ∈ A
(D) Φ ∈ A
हल:
(C) 4 ∈ A

प्रश्न 3.
A = {a, e, i, o, u} तथा B = {i, o} हों, तब सत्य है-.
(A) A ⊂ B
(B) B ⊂ A
(C) A = B
(D) A तुल्य B
हल:
(B) B ⊂ A

प्रश्न 4.
A ∩ (A ∪ A)' बराबर है-
(A) A
(B) A'
(C) Φ
(D) U
हल:
(C) Φ

प्रश्न 5.
यदि U = {1, 2, 3, 4, 5, 6} तथा A = {1, 2, 3, 4, 5, 6} हों एवं C ∩ A = {2} हो, तो समुच्चय C है-
(A) {2}
(B) {2, 3}
(C) U
(D) A
हल:
(A) {2}

प्रश्न 6.
यदि A = {x/x² = 4} तथा B = {x/x² - 5x + 6 = 0} हो, तो A ∪ B है -
(A) {2, 3}
(B) {- 2, 3}
(C) {2, -3}
(D) {- 2, 2, 3}
हल:
(D) {- 2, 2, 3}

प्रश्न 7.
सम अभाज्य संख्याओं (प्राकृत) की संख्या है-
(A) एक
(C) दो
(B) तीन
(D) शून्य
हल:
(A) एक

प्रश्न 8.
A = {x : x, attract शब्द के अक्षर हैं},
B = {y : y, cataract शब्द अक्षर हैं}, तो—
(A) A ≠ B
(B) B ⊂ A
(C) A ⊂ B
(D) A = B
हल:
(D) A = B

प्रश्न 9.
यदि A = {2, 0, - 2 } तथा B = {x : x ∈ z पूर्णांक), x⁴ - 4x² = 0} हो, तो-
(A) A ≠ B
(B) A ⊂ B
(C) A = B
(D) B ⊂ A
हल:
(C) A = B

प्रश्न 10.
n अवयवों वाले समुच्चय के उपसमुच्चय की संख्या होती है—
(A) 2ⁿ
(B) 2 × n
(C) n²
(D) \(\frac{2}{n}\)
हल:
(A) 2ⁿ

प्रश्न 11.
‘ALLAHABAD' शब्द में आए स्वरों का समुच्चय है-
(A) {A, A, A, A}
(B) {A}
(C) {L, L, H, B, D}
(D) {A, L, H, B, D}
हल:
(B) {A}

प्रश्न 12.
यदि x = {a, e, i, o, u} तथा y = {a, o, u} हो, तो x - y का मान होगा
(A) {a, e, i}
(B) {0, u}
(C) {e, i}
(D) {e, i, 0}
हल:
(C) {e, i}

प्रश्न 13.
यदि ∪ सार्वत्रिक समुच्चय हो तथा A एक अरिक्त समुच्चय हो, तो निम्नलिखित में से कौनसा कथन सत्य है-
(A) A ∪ A′ = ∪
(C) A ∩ A = 0
(B) A ∪ Φ = Φ
(D) A ∪ A' = Φ
हल:
(A) A ∪ A′ = ∪

प्रश्न 14.
यदि A और B दो समुच्चय हैं तो A ∩ (A ∪ B) का मान होगा-
(A) A
(B) Φ
(C) B
(D) कोई नहीं
हल:
(A) A

प्रश्न 15.
निम्नलिखित में से परिमित समुच्चय है-
(A) {x : x ∈ N}
(B) {x : x > 10 x ∈ N}
(C) {x : x < 10, x ∈ N}
(D) {x : x = 2n, n ∈ N}
हल:
(C) {x : x < 10, x ∈ N}

प्रश्न 16.
यदि U = {1, 2, 3, 4, 5, 6} तथा A = {1, 2, 3, 4, 5, 6} हो, तो A' बराबर होगा-
(A) {0}
(B) {1, 2, 3}
(C) Φ
(D) {4, 5, 6}
हल:
(C) Φ

प्रश्न 17.
निम्नलिखित में से कौनसा अपरिमित समुच्चय है-
(A) {x : x ∈ N तथा x ≥ 10}
(B) {x x ∈N और x < 10}
(C) {x : x ∈ N और 10 ≤ x ≤ 100}
(D) {x : x ∈ N तथा x < 1000}
हल:
(A) {x : x ∈ N तथा x ≥ 10}

प्रश्न 18.
यदि A, B दो समुच्चय हैं, तब (A ∪ B)' बराबर है --
(A) A ∩ B
(B) A ∪ B
(C) A' ∩ B'
(D) A' ∪ B’
हल:
(C) A' ∩ B'

प्रश्न 19.
यदि समुच्चय A में m अवयव हो, A के घात समुच्चय में अवयवों की संख्या है-
(A) m²
(B) 2^m
(C) 2^2m
(D) 2^m+1
हल:
(B) 2^m

प्रश्न 20.
एक महाविद्यालय के 300 छात्रों में से प्रत्येक छात्र 5 समाचार - पत्र पढ़ते हैं तथा प्रत्येक समाचार-पत्र 60 छात्रों द्वारा पढ़ा जाता है तब समाचार-पत्रों की संख्या होगी—
(A) कम से कम 30
(B) अधिक से अधिक 20
(C) 25
(D) इनमें से कोई नहीं
हल:
(A) कम से कम 30

रिक्त स्थानों की पूर्ति करो—

प्रश्न 1.
वस्तुओं के ...................................... संग्रह को समुच्चय कहते हैं।
हल:
सुपरिभाषित

प्रश्न 2.
यदि a, समुच्चय A का अवयव है तो इसे a ..................... A लिखते हैं।
हल:
∈

प्रश्न 3.
किसी समुच्चय को निरूपित करने की .................................. विधियाँ हैं|
हल:
दो

प्रश्न 4.
पूर्ण संख्याओं के समुच्चय को ................................... से व्यक्त करते हैं
हल:
W

प्रश्न 5.
अपरिमेय संख्याओं के समुच्चय को ............................. से व्यक्त करते हैं।
हल:
T

प्रश्न 6.
एक समुच्चय जिसमें एक भी अवयव नहीं होता, ..................................... समुच्चय कहलाता है
हल:
रिक्त

प्रश्न 7.
यदि समुच्चय A का प्रत्येक अवयव, समुच्चय B का भी एक अवयव है, तो A, B का ............................... कहलाता है।
हल:
उपसमुच्चय

प्रश्न 8.
यदि समुच्चय A में केवल एक अवयव हो, तो इसे .............................. समुच्चय कहते हैं।
हल:
एकल

प्रश्न 9.
A ⊂ B तथा A ≠ B तो A, B का उचित ........................... कहलाता हैं।
हल:
उपसमुच्चय

प्रश्न 10.
समुच्चय A के उपसमुच्चयों के संग्रह को A का ............................ समुच्चय कहलाता है।
हल:
उत्तरमाला
घात।

निम्नलिखित कथनों के लिए सत्य / असत्य लिखिए-

प्रश्न 1.
समुच्चय A तथा B के लिए A - B ≠ B – A
हल:
सत्य

प्रश्न 2.
A ∪ B ≠ B ∪ A
हल:
असत्य

प्रश्न 3.
A ∪ (B ∪ C) = (A ∪ B) ∪ c
हल:
सत्य

प्रश्न 4.
यदि A सार्वत्रिक समुच्चय ∪ का एक उपसमुच्चय है, तो इसका पूरक A ́ भी ∪ का एक उपसमुच्चय होता है
हल:
सत्य

प्रश्न 5.
De Morgan का नियम है– (A ∪ B) = A ́ ∪ B ́
हल:
असत्य

प्रश्न 6.
यदि A और B ऐसे परिमित समुच्चय हैं कि A ∩ B = Φ तो n(A ∪ B) = n(A) + n(B)
हल:
सत्य

प्रश्न 7.
यदि A = Φ तब P(A) = {Φ} = n(A) + n(B)
हल:
सत्य

प्रश्न 8.
यदि A और B दो समुच्चय हैं, तब (A ∪ B)' ∩(A′ ∪ B)′ = {0}
हल:
असत्य

प्रश्न 9.
यदि [a, b] = a ≤ x ≤ b, x ∈ R
हल:
सत्य

प्रश्न 10.
वास्तविक संख्याओं के समुच्चय को V से व्यक्त करते हैं।
हल:
असत्य

सही मिलान कीजिए-

भाग (A)	भांग (B)
1. 3 अवयवों वाले समुच्चय के उपसमुच्चयों की संख्या	(a) वर्गसम नियम
2. तीन समुच्चयों A, B व C के लिए A ∪ (B ∪ C) बराबर है।	(b) R
3. A ∪ Φ = A	(c) 23
4. अन्तराल (-∞, ∞) के समान समुच्चय	(d) क्रमविनिमेयता
5. A ∩ B = B ∩ A	(e) np' (A) = 2n
6. यदि n (A) = n तब.	(f) बंटन नियम
7. A ∩Φ	(g) (A ∪ B) ∪ (A ∪ C)
8. A ∪ A = A	(h) समुच्चयों का अन्तर
9. A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)	(i) तत्समक नियम
10. A -  B = {xlx ← A और x ∉  Φ}	(j) Φ

हल: 
1. (c)
2. (g)
3. (i)
4. (b)
5. (d)
6. (e)
7. (j)
8. (a)
9. (i)
10. (h)