RBSE 11th Geography Practical Book Solutions Chapter 4 Map Projections

Rajasthan Board RBSE Solutions for Class 11 Geography Practical Book Chapter 4 Map Projections

RBSE 11th Geography Practical Book Solutions Chapter 4 Map Projections

RBSE Class 11 Geography Map Projections Textbook Questions and Answers

Multiple Choice Questions

1. Choose the right answer from the four alternatives given below:
(i) A map projection least suitable for the world map:
(a) Mercator 
(b) Simple Cylindrical
(c) Conical 
(d) All the above
Answer: 
(c) Conical.

 

(ii) A map projection that is neither the equal area nor the correct shape and even the directions are also incorrect.
(a) Simple Conical 
(b) Polar zenithal
(c) Mercator 
(d) Cylindrical
Answer: 
(d) Cylindrical.

(iii) A map projection having correct direction and correct shape but area greatly exaggerated polewards is
(a) Cylindrical Equal Area 
(b) Mercator
(c) Conical
(d) All the above
Answer: 
(b) Mercator.

(iv) When the source of light is placed at the centre of the globe, the resultant projection is called.
(a) Orthographic 
(b) Stereographic
(c) Gnomonic 
(d) All the above
Answer: 
(c) Gnomonic.

2. Answer the following questions in about 30 words:

I. Describe the elements of map projection.
Answer: 
The elements of map projection are as following:

1. Reduced earth: The earth’s model is represented with the help of a reduced scale on a flat sheet of paper on this model the network of graticule can be translated.
2. Parallels of latitude: These are the circles round the globe parallel to the equator and maintaining uniform distance from the poles. They are demarcated as 0° to 90° North and South.
3. Meridians of longitudes: Longitues are the elements of map projections. There are also drawn north to south direction from one pole to another and two opposite meridians make a complete circle.
4. Global property: Distance between any given points of a region shape of the region, size or area of the region in accuracy are given in it.

II. What do you mean by global property?
Answer: 
The global property means the

1. Correctners of the area
2. Direction
3. Distance
4. and shape of the area.

III. Not a single map projection represents the globe truly. Why?
Answer: 
Map projection project the network of latitudes and longitudes on a plain surface by using the geometrical and mathematical methods. The globe is the true representation of earth. The projections given a shadowed picture of the globe which is distorted in those parts which are further away from the point where the paper touches the globe.

IV. How is the area kept equal in cylindrical equal-area projection?
Answer: 
The area is kept equal in cylindrical equal area projection because the parallels and meridians are projected as straight lines intersecting one another at right angles.

3. Differentiate between:

I. Developed and non-developed surface.
Answer: 
Developed Surface: A developed surface is a surface which can be unrolled into a plane surface. For e.g. a plane, a cylinder and a cone are developable surfaces. Undeveloped surface: An undeveloped surface can not unroll into a place just as a globe.

II. Homolographic and Orthographic projections.
Answer: 
Homolographic projection: These are the projections which are graticule of latitudes and longitudes on the map its equal in area. Orthographic Projection: On these projections the correct shape of the area of a country is shown.

III. Normal and Oblique projections. Ans

Normal Projections	Oblique Project ion
In these projections the longitudes are drawn prependicular on latitudes on right angles.	In these projections in inner surface of the cone touches some parallel known as standered parallel.
These are known as cylinderical projections.	These are known as conical projections.

IV. Parallels of latitudes and meridians of longitues.
Answer:

Parallel of Latitude	Meridians of Longitude
1. Latitudes is the angular distance of a place North or South of the equator.	1. Longitudes is the angular distance of a place. Easter west of Prime Meridian.
2. The latitude value increases in North South direction from the equator.	2. The longitude value increases in East- West Directions from the Meridian.
3. Its value ranges between 0° to 90° N, 0° to 90° S.	3. Its value ranges between 0° to 180° E, 0° to 180° W.

4. Answer the following questions in not more than 125 words.

I. Discuss the criteria used for classifying map projection and state the major characteristics of each type of projection.
Answer: 
Map Projections: Globe is the best and accurate model of the earth. There are many problems in representing the spherical globe on a flat sheet of paper. Map projections are the means of transferring the lines of latitude and lines of longitude of the globe on to a flat sheet of paper. The expansion of a photograph on a screen in a cinema hall is an example of Projection. By this method, the lines of latitude and lines of longitude are projected on a flat sheet of paper. Classification of map projections: Different types of map projections are used.

These are classified on the following bases:

1. On the basis of source of light:
On this basis, the projections are of two types:
(a) Perspective projections
(b) Non-Perspective projections. 

(a) Perspective projections are prepared on the basis of Geometry. In these projections, shadow of lines of latitude and longitude are drawn on the basis of the location of source of light. Source of light can be placed at different positions.

(b) Non-perspective projections:
are called mathematical projections. In these projections, source of light is not used. Principles of mathematics are used to draw these projections.

2. On the basis of purpose:
(a) Equal-area Projection: 
With the help of these projections, the equal-area property of a map is preserved. These are called Homolographic projections also. These are used for preparing distribution maps.

(b) Orthomorphic Projections: 
On these projections, the correct shape of an area or a country is shown.

(c) Azimuthal Projections: 
These map projections help to preserve the property of correct direction on a map. These are used for preparing maps for sailors and for air-navigators.

3. On the basis of construction:
(a) Cylindrical Projections: 
In these projections, it is imagined that a hollow cylinder circumscribes the globe. The equator of the globe touches the cylinder so that the length of the equator remains correct. In this group, the following non-perspective projections are included:

• Simple cylindrical projection
• Cylindrical equal area projection
• Mercator’s projection

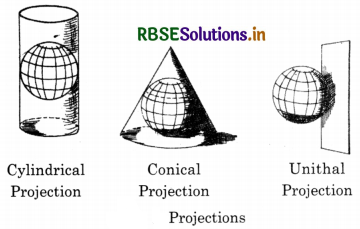
In these projections, lines of latitude are parallel to the equator and are straight lines. The meridians are vertical straight-lines. These lines intersect each other at right angles.
(b) Conical Projections: 
In this projection, the cone is used as a surface. It is imagined that the cone is placed on the globe so that its vertex is above the pole. The axis of the cone coincides with that of the globe. The parallel along which the cone touches the globe is called the standard parallel. It keeps correct length. The parallels are shown by concentric arcs of circles. Meridians are straight lines drawn at equal angular distance. In this group, the following map projections are included:

• Simple Conical Projection with one standard parallel.
• Conical Projection with two standard parallels
• Bonne’s Projection
• Polyconic Projection.

(c) Zenithal Projections: 
In these projections, it is assumed that a plane surface is placed tangentially at the pole of the globe. These are azimuthal projections showing correct bearing. These are used for polar areas. According to the position of the source of light, these projections are perspective projections.

• Polar Zenithal Gnomonic Projection.
• Polar Zenithal stereographic Projection.
• Polar Zenithal orthographic Projection.

In this group, two non-perspective zenithal projections of zenithal equidistant projection and zenithal equal area projection are also included.
(d) Conventional Projection: 
These projections are mathematical projections. These are called conventional projections, because no surface is used in these. These are drawn for specific purpose of drawing world maps. These include the Sinusoidal projection and Mollweide’s projections.

Importance of Map Projections:

• Map projections are useful for drawing maps on a flat sheet of paper.
• These provide knowledge about the true shape of the earth.
• Atlas maps and wall maps are prepared on the basis of map projections.
• Different types of maps are prepared with the help of map projections.
• These help us to know the location of lines of latitude and lines of longitude.
• Map projections are used to draw distribution maps, political maps, and maps of ocean routes, air routes and ocean currents.

II. Which map projection is very useful for navigational pruposers? Explain the main properties and limitations of this projection?
Answer: 
The Mercater projection is an orthomorphic projection and very useful for the navigational purposes. The properties and limitations are as under:
Properties of Mercator’s Projection:

1. It is a cylindrical projection which was developed by a Dutch Cartographer Mercator in 1569.
2. It is a non-perspective projection.
3. The parallels are straight lines parallel and equal to Equator.
4. Meridians are perpendiculars drawn at equal distances.
5. Meridians and parallels intersect at right-angles.
6. Scale along equator is correct. But it increases along other parallels as we move towards poles. Pole is a point but it is drawn equal to equator. So, it is exaggerated infinite.
7. Scale along meridians is also exaggerated. 

Limitations: 

1. Poles can not be shown on this projection. 
2. The scale in polar area is exaggerated many times. So the area is increased in polar areas.

III. Discuss the main properties of conical projection with one standard parallel and discribe its major limitations.
Answer: 
Properties: 

1. The Pole and all the lines of latitude are concentric arcs of circles.
2. Meridians are straight lines radiating from the vertex.
3. Parallels intersect Meridians at right angles.

Merits: 
Scale along the standard parallel is correct. Projection is satisfactory for areas in the neighbourhood of standard parallel.

Demerits:
This projection is neither equal in area nor in orthomorphic. It is not azimuthal. Uses: This projection is useful for small areas with small north-south extent, but not for a large east-west extent such as Trans-Siberian Railway. 

RBSE Class 11 Geography Map Projections Important Questions and Answers

Essay Type Questions

Question 1. 
Define the term map projection, classify map projections. Explain their importance.
Answer: 
Map Projections : Globe is the best and accurate model of the earth. There are many problems in representing the spherical globe on a flat sheet of paper. Map projections are the means of transferring the lines of latitude and lines of longitude of the globe on to a flat sheet of paper. The expansion of a photograph on a screen in a cinema hall is an example of Projection. By this method, the lines of latitude and lines of longitude are projected on a flat sheet of paper.

Classification of map projections : 
Different types of map projections are used. These are classified on the following bases :
1. On the basis of source of light: 
On this basis, the projections are of two types :
(a) Perspective projections
(b) Non-Perspective projections. 

(a) Perspective projections:
are prepared on the basis of Geometry. In these projections, shadow of lines of latitude and longitude are drawn on the basis of the location of source of light. Source of light can be placed at different positions. 

(b) Non-perspective projections:
are called mathematical projections. In these projections, source of light is not used. Principles of mathematics are used to draw these projections.

2. On the basis of purpose :
(a) Equal-area Projection: With the help of these projections, the equal-area property of a map is preserved. These are called Homolographic projections also. These are used for preparing distribution maps.
(b) Orthomorphic Projections: On these projections, the correct shape of an area or a country is shown.
(c) Azimuthal Projections: These map projections help to preserve the property of correct direction on a map. These are used for preparing maps for sailors and for air-navigators.

3. On the basis of construction :
(a) Cylindrical Projections: In these projections, it is imagined that a hollow cylinder circumscribes the globe. The equator of the globe touches the cylinder so that the length of the equator remains correct. In this group, the following non-perspective projections are included :

• Simple cylindrical projection
• Cylindrical equal area projection
• Mercator’s projection.

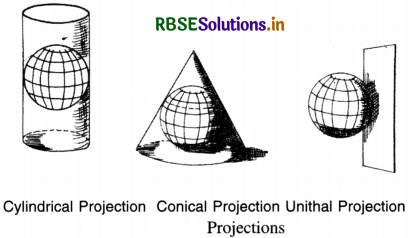
In these projections, lines of latitude are parallel to the equator and are straight lines. The meridians are vertical straight-lines. These lines intersect each other at right angles.

(b) Conical Projections : 
In this projection, the cone is used as a surface. It is imagined that the cone is placed on the globe so that its vertex is above the pole. The axis of the cone coincides with that of the 
globe. The parallel along which the cone touches the globe is called the standard parallel. It keeps correct length. The parallels are shown by concentric arcs of circles. Meridians are straight lines drawn at equal angular distance.
In this group, the following map projections are included :

• Simple Conical Projection with one standard parallel.
• Conical Projection with two standard parallels
• Bonne’s Projection
• Polyconic Projection.

(c) Zenithal Projections : 
In these projections, it is assumed that a plane surface is placed tangentially at the pole of the globe. These are azimuthal projections showing correct bearing. These are used for polar areas. According to the position of the source of light, these projections are perspective projections.

1. Polar Zenithal Gnomonic Projection.
2. Polar Zenithal stereographic Projection.
3. Polar Zenithal orthographic Projection.

In this group, two non-perspective zenithal projections of zenithal equidistant projection and zenithal equal area projection are also included.

(d) Conventional Projection : 
These projections are mathematical projections. These are called conventional projections, because no surface is used in these. These are drawn for specific purpose of drawing world maps. These include the Sinusoidal projection and Mollweide’s projections.

Importance of Map Projections:

1. Map projections are useful for drawing maps on a flat sheet of paper.
2. These provide knowledge about the true shape of the earth.
3. Atlas maps and wall maps are prepared on the basis of map projections.
4. Different types of maps are prepared with the help of map projections.
5. These help us to know the location of lines of latitude and lines of longitude.
6. Map projections are used to draw distribution maps, political maps, and maps of ocean routes, air routes and ocean currents.

Question 2. 
What is the necessity of map projection? State the qualities of a good projection.
Answer: 
Globe is an undevelopable surface. It is not possible to show it on a plane surface. If it is traced on a flat sheet of paper, many folds and creases will be formed. If a tracing paper is covered around a globe, it does not fit exactly when it is opened. The areas near the poles will be shown very apart. Therefore the shape, area, distance, direction of an area cannot be shown correctly on a map. Therefore some methods are used to get the maximum accuracy. These methods are called map projections. If the globe were a developable surface, there would have been no necessity of map projection

Question 3. 
Write short notes on :
(i) Developable surfaces
(ii) Undevelopable surfaces
(iii) Map and Globe
(iv) Grid, Gore and Zone.
Answer: 
(i) Developable surface : 
A developed surface is a surface which can be unrolled into a plane surface. For example a plane, a cylinder and a cone are developable surfaces. If a cylinder is cut open from one end to the other vertically, it is a developable surface. If a cone is cut open from apex to bas, it becomes a plane.

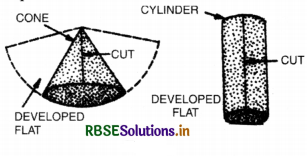
(ii) Undeveloped surface : An undeveloped surface can not unroll into a place just as a globe.

(iii) Comparison between a map and globe : 
Globe is a true model of the earth. But it can not be used conveniently in practice. There are many problems :
(a) A globe is not portable, while a map can be rolled.
(b) Only one hemisphere of globe is visible at one time.
(c) It is not easy to measure the distance on curved surface of the globe.
(d) It is difficult to make a globe on a large scale,
(e) Data cannot be shown on a globe.
(f) It is not possible to trace any part of globe.

(iv) Grid, Gore and Zone : 
The network formed by lines of latitude and longitude on a map is called Grid. The vertical area covered by two adjacent lines of longitude is called a gore, the area covered by two adjaceent lines of latitude is called a zone.

Question 4. 
Explain why no projection represents the globe truly?
Answer: 
Globe being a sphere is three demensional surface. It cannot be transferred truly on a two dimensional map. Therefore no projection is perfect. To achieve different purposes, different map projections are used. On one map it is not possible to have correct-shape, equal area and correctdirection at the same time.

Question 5. 
What points are to be considered while; drawing Map Projections? 
Answer: 
Drawing of Map-Projections For drawing of map projections, the following basic points be considered :
(1) Radius of the globe : The actual radius of the earth is 3960 miles or 250,000,000 inches. On this scale the radius of globe is calculated on

Radius \(=\frac{\text { Actual radius of earth }}{\text { R.F. of Map }}\)

If R.F. is \(\frac{1}{250,000,000}\) 

Then Radius of globe \(=\frac{250,000,000}{125,000,000}=\frac{250 \mathrm{M}}{125 \mathrm{M}}=2^{\prime \prime}\)

In Centimetres: Radius of the earth is 6366 kms.
= 636,600,000 cms.
For convenience it is rounded as 625 M

If scale is \(\frac{1}{125 \mathrm{M}}\) then Radius = R = \(\frac{625,000,000}{125,000,000}\)

= 5 cms.

(2) Interval: The difference between two adjacent lines of latitude is called parallel interval. The difference between two adjacent lines of longitude is called Meridian interval.

(3) Extent of the area : It is important to know the East-West and North-South extent of an area.

(4) Basic Parallels and Meridians : Some projections are drawn with equator as the base such as cylindrical projection. But in conical projections a standard parallel is the basic parallel. In Zenithal projections 90°N and 90° South are the centre of projection.

CONICAL PROJECTION WITH ONE STANDARD PARALLEL

Question 1. 
Draw a Conical projection with one standard parallel on a scale of 1:125,000,000 when parallel interval is 15°; meridian interval 30° and standard parallel is 45°.
Answer: 
Construction :
Radius of the earth =img 
Select a standard parallel of 45° because it is in the middle of the area. Draw a circle with a radius of 2". Draw an angle of 45° within this circle. Draw a tangent at angle of 45° and make it to meet the polar axis. Draw an angle of 15° arc draw a semicircle at the centre of the circle it will intersect the standard parallel at T. Draw a perpendicular to polar axis. This line will be equal to the Meridian interval of 15°. Now draw a perpendicular line (W) apart for drawing network on this projections. Draw the Standard parallel as an arc by taking radius of tangent already drawn. Mark off at equal distances the distance between parallels (arc of 15°). Draw concentric areas of circles from V as the centre. These will represent lines of latitude. Draw meridians as straight lines by joining the V and the points marked on standard parallel with 15° arc distance.

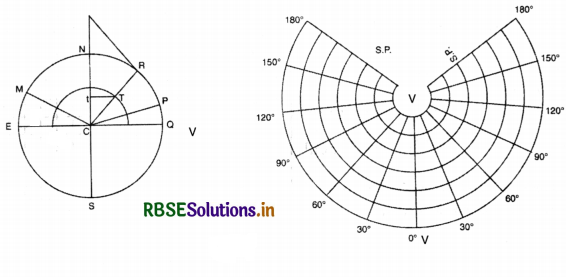
Properties: 

• The Pole and all the lines of latitude are concentric arcs of circles.
• Meridians are straight lines radiating from the vertex.
• Parallels intersect Meridians at right angles.

Merits :
The scale along the standard parallel is correct.
Projection is satisfactory for areas in the neighbourhood of standard parallel. 

Demerits:
This projection is neither equal in area nor in orthomorphic. It is not azimuthal.
Uses: This projection is useful for small areas with small north-south extent, but not for a large east-west extent such as Trans-Siberian Railway.

Question 2. 
Draw a Mercator’s projection on a scale; of 1:125,000,000 when the parallel and meridian j interval is 20°. Describe the properties of! Mercator’s projection.
Answer: 
The radius of the reduced earth
\(=\frac{125,000,000}{250,000,000}=2^{\prime \prime}\)

Length of the equator = l = 2πR = \(2 \times \frac{22}{7} \times 2^{\prime \prime}\) 

\(=\frac{88}{7}{ }^{\prime \prime}=12.6^{\prime \prime}\)

The number of meridians = \(\frac{360}{20}=18\) 

The distance for 20 - meridian Interval 

\(=\frac{12.6}{18}=0.7^{\prime \prime}\)

Drawing of Meridians:
Draw a line 12.6” long. It shows the equator. Divide the equator into 18 equal parts by geometrical method (or by taking 0.7” as distance between 2 meridians). Draw perpendiculars through these points. These represent meridians were:

Drawing of parallels:
The distance of any parallel from the equator r can be calculated with the help of the following table 

Distance of parallels from the Equator
(r = radius of the reduced earth)

Latitude	Distance from the Equato	r=radius of  the globe 2”
20°	0.356 × r	0.356 × 2” = 0.712”
40°	0.763 × r	0.763 × 2” = L526”
60°	1.317 × r	1.317 × 2” 2.634”
80°	2.437 × r	2.437 × 2” = 4.874”
90°	∞	∞

Draw a line 1 = 12.6” long to represent the Equator. Mark a distance of 0.712” from the equator towards north and south. Draw a line parallel through these to show 20° latitude. Mark off distances 1.526”, 2.634”, 4.874” to draw the parallels of 40°, 60°, 80°. Number the parallels and meridians (180° East to 180° West) and (80° N to 80°S).

Properties of Mercator’s Projection:

1. It is a cylindrical projection which was developed by a Dutch Cartographer Mercator in 1569.
2. It is a non-perspective projection.
3. The parallels are straight lines parallel and equal to Equator.
4. Meridians are perpendiculars drawn at equal distances.
5. Meridians and parallels intersect at right-angles.
6. Scale along equator is correct. But it increases along other parallels as we move towards poles. Pole is a point but it is drawn equal to equator. So, it is exaggerated infinite.
7. Scale along meridians is also exaggerated.

 Merits : 
(1) The scale along the equator is true.

(2) The parallels and meridians intersect at right angles. So at any point, the parallel scale is equal to meridian scale. So the shape of small areas is correct. It is an orthomorphic projections.

(3) It is an Azimuthal projection. Any straight line drawn in this network intersects the parallels and meridians at the same angle. It is called a Loxodrome or Rhumb line. Loxodrome is a line of constant and true bearing.

Demerits : 

1. Poles can not be shown on this projection.
2. The scale in polar area is exaggerated many times. So the area is increased in polar areas.

Merits :

1. It is used for navigation and aviation due to correct bearing.
2. Mercator charts, due to correct bearing, are used to show ocean currents, winds.
3. World maps on Atlases and wall maps are drawn on this projection.
4. Due to correct shape, the political map of any country can be shown on this projection.

Question 3. 
Why Mercator Projection is very useful for navigational purposes?
Answer: 
Mercator is an orthomorphic (correct shape) projection-Any straight line drawn on this projection intersects all the lines of latitude and longitude at same and constant angles. This line is called a line of constant bearing or Roxodrome or Rhumb line as it is shown in the figure. 

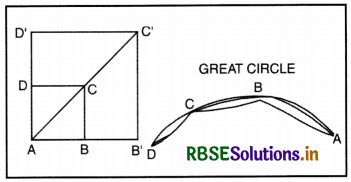
AB is a part of equator and CD is a part of any other parallel. The diagonal AC shows the direction. Both the paralled scale and meridian scale are increased in the same ratio to get correct direction. The new direction AC' is same as AC direction. On Mercator projection, straight line shows constant and correct bearings. The sailors sail their ships in a constant direction. They reach their destination without changing their direction. They follow great circles (shortest route). These are curved. The great circle is sub-divided into sections. In each section, a constant direction is followed. So this projection is useful for navigation.

Question 4. 
On what factors does the choice of projections depend?
Answer: 
Choice of Projection
Different types of projections are prepared on the basis of purpose. The choice of projection depends upon:

1. Purpose of the map, 
2. Extent of the map and 
3. Ease of Drawing.

1. On the basis of purpose of the map : 

• For distribution of maps, equal area projections are used. For this cylindrical equal area and Mollweide’s projections are used.
• Mercator projection is used for showing correct shape of an area.
• For showing ocean routes, air routes, correct bearing is necessary. For this, Mercator projection is used 
• Zenithal projections are used for Polar areas.

2. On the basis of extent of map.

• For world maps. Mollweide, Mercator Projections.
• For continents: Bonne’s Projection
• For a large country: Conical Projection with two S.P.
• For a small area: Conical with one S.P. Projection.
• For equatorial areas: Cylindrical Projections.
• For areas with large North-South extent: Conical Projections. 

QUESTIONS FOR VIVA-VOCE  

Question 1. 
What is the shape of the globe?
Answer: 
Three-dimensional sphere.

Question 2. 
What is the shape of a map?
Answer: 
Two dimensional.

Question 3. 
Give two examples of developable surface. 
Answer: 
Cylinder and cone.

Question 4. 
Which Projection is suitable to show areas around equator?
Answer: 
Mercator Projection. 

Question 5. 
Why can’t the globe be developed on a flat surface?
Answer: 
Due to curvature.

Question 6. 
Name the qualities of a perfect map. 
Answer: 
Correct area, correct shape, correct direction and distance.

Question 7. 
What is the total number of parallels?
Answer:
90° N and 90° S.

Question 8. 
What is the total number of meridians T?
Answer: 
180° E and 180° W. 

Question 9. 
Which is the longest line of latitude?
Answer: 
Equator.

Question 10. 
Give two examples of Great circles.
Answer:
Equator and meridians were:

Question 11. 
What do you mean by zenith?
Answer: 
The highest point in the sky.

Question 12.
What is the radius of the earth?
Answer: 
250,000,000 inches.

Question 13. 
State the rule for finding out the length; of the equator. 
Answer: 
I = 2πR.

Question 14. 
Name an equal area projection.
Answer: 
Cylindrical equal area projection.

Question 15. 
Name an orthomorphic projection.
Answer: 
Mercator’s projection.  

Question 16. 
Which projections are used for polar areas?
Answer: 
Zenithal projections.

Question 17. 
What is the demerit of Cylindrical Projections?
Answer: 
The scale along parallels is increased.

Question 18. 
What is the Standard Parallel?
Answer: 
A parallel which keeps its correct length.

Question 19. 
Which surfaces are used for preparing Projections?
Answer: 
Cylinder, Cone, a Plane.

Question 20. 
Which projection is used for showing distribution of crop maps?
Answer: 
Cylindrical equal area projection.

Question 21. 
Which projection is used for showing Trans-Siberian Railway?
Answer: 
Conical projection with one Standard Parallel.