RBSE 11th Geography Practical Book Solutions Chapter 2 Map Scale

Rajasthan Board RBSE Solutions for Class 11 Geography Practical Book Chapter 2 Map Scale Textbook Exercise Questions and Answers.

RBSE 11th Geography Practical Book Solutions Chapter 2 Map Scale

RBSE Class 11 Geography Map Scale Textbook Questions and Answers

Multiple Choice Questions

1. Choose the right Answer out of the four alternatives given :
(i) Which one of the following methods of scale is a universal method?
(a) Simple Statement
(b) Representative Fraction
(c) Graphical Scale
(d) None of the above
Answer: 
(a) Representative Fraction.

 

(ii) Map distance in a scale is also known as :
(a) Numerator
(b) Denominator
(c) Statement of Scale
(d) Representative Fraction.
Answer: 
(a) Numerator.

(iii) ‘Numerator’ in scale represents:
(a) Ground distance 
(b) Map distance 
(c) Both the distance 
(d) None of the above 
Answer: 
(b) Map distance.

Short Answer Type Questions

2. Answer the following questions in about 30 words :
(i) What are the two different systems of measurement?
Answer: 
Metric and British.

(ii) Give one example each of statement of scale in Metric and English system.
Answer: 
1 metre : 100 cms, 1" : 6 inch.

(iii) Why is the Representative Fraction method called a Universal method?
Answer: 
It can be used in any measurement system.

(iv) What are the major advantages of the graphical method?
Answer: 
It can be used is measure distance on a scale.

3. Convert the given statement of scale into representative fraction (RF) :
(i) 5 cm represents 10 km.Answer: 
1 kilometre = 1,00,000 cm.
10 km = 10,00,000 cm
So, 5 cm = 10,00,000 cm (10 km = 10,00,000 cm)
\(1 \mathrm{~cm}=\frac{10,00,000}{5}=2,00,000 \mathrm{~cm}\)
So, 1 cm 2,00.000 cm
R.f = 1:2,00,000
(ii) 2 inch represents I mile
Answer: 
1 mile = 63,360 inch
∴ 4 mile = 63,360 X 4 = 2,53,440 inch
So, 2 inch = 2,53,440 inch
\(1 \text { inch }=\frac{2,53,440}{2}=1,26,720 \text { inch }\)

Ref = 1:1,26,720
(iii) 1 inch represents 1 yard
Answer:
1 yard = 36 inch R.F = 1:36

(iv) 1 cm represents loo metres
Answer:
1 cm = 10,000 cm
1 metre = 10,000 cm
R: F= 1:10,000

4. Convert the given R.F into the statement of scale in the system of measurements shown in parentheses :
(i) 1:100,000 (into km)

(i) 1:100,000 (into km)
Answer:
1 cm, represents 1 km.
Because, 1 km = 1,00,000 cm

(ii) 1:31,680 (into furlongs)
Answer:
1 inch represents 4 furlongs
Because, 1 furlong-7, 920 inch
So 31,680 inch 4 furlong.

(iii) 1:126,720 (into miles)
Answer:
1 inch represents 2 mile
Because, 1 mile = 63,360 inch
So, 1,26,726 inch = 2 mile

(iv) 1:50,000 (into metres).
Answer:
1 cm represents 500 metre
Because 1 mitre = lOO cm
So, 50,000 cm = 500 metre
Because = 1 km = 1,00,000 cm.

5. Construct a graphical scale when the given R.F is 1:50,000 and react the distances in kilometre and metre.
Answer: 
Following steps may be followed to get the length of line for a graphical scale. Meaning of 1:50,000 is 1 unit of the may represents 50,0 ground units meAnswer:1 cm represents 50,000 cm. or 15 cm = 50,000 x 15/100,000 km. or 15 cm = 7.5 km.

Because 7.5 km is not a round number, so we can choose 5 or 10 (km) as a round number. In this question we choose 5 as the round number For the length determination of the line to show 5 km following calculations to be carried our.
7.5 km represented by a line of 15 cm
5 km represented by a line of 15 x 5/7.5
Construction some steps are:

1. Firestly grow a line of 10 cm (straight line) and divide this into sequal parts and assign a value of 1 km each for 4 right side divisions from 0 mark.

2. Now divide the left side division as 10 equal parts and mark every division by a value of 100 metres, start from 0.

each of the sub-division from 0. when the given statement of scale is 1 inch representing 1 mile construct a graphical scale & read the distances in miles or furlongs. 

RBSE Class 11 Geography Map Scale Important Questions and Answers

Short Answer Type Questions 

Question 1. 
Define the term ‘Scale’.
Answer: 
Scale is the map-land ratio. Map distance and Ground distance always bear a ratio. Scale is a ratio which a distance between two points on a map bears to the actual distance between the corresponding (same) points on the ground. Example. If a map has a scale of 1 cm : 5 kms. it means we that one centimetre on the map represents a (stance of five kilometres on the ground)

Question 2. 
What is the necessity of ‘Scale’? 
Answer:

1. 'Scale's 'the' most important essential of a map. Without scale, we have only a sketch or a diagram and not a geographic map.
2. It is necessary to draw a scale to show the relative position of different places on the map.
3. Every map has a definite ratio to the earth. It is not possible to make the map of the same size because 25000 miles or 40000 kms of paper will be required to draw the equator.
4. Maps are generally reduced in size. They are said to be drawn to scale. Thus, scale is a necessity in drawing of a map.

Question 3. 
Distinguish between small scales and large scales.
Answer:

1. Small scales are scales of miles to the inch. The larger the number of miles, the smaller is the scale.	1. Large scales are scales of inches to the mile. The smaller the number of miles, the larger is the scale.
2. For example, 1 cm: 10 km 1 inch : 60 miles.	2. For example, 10cm: 1 km  6 inches :1 mile
3. In this, one cm shows a distance more than 1 km.	3. In this, one km. is shown by a length more than 1cm.
4. Atlas maps, wall maps are on small scales.	4. Cadastral maps are on large scales.
5. These maps do not show details of an area.	5. These maps show details of an area.
6. These are called small scales due to smaller size of the map.	6. These are called large scale, due to larger size of the map.
7. If R.F. given, the small scales have a larger denominator.	7. If R.F. is given, the large scale have the smaller denominator.

Question 4. 
Explain the importance of scale.
Answer: 
Scale is the most important item in the study of cartography.

1. With the help of scale, we can represent large areas in a reduced shape and size.
2. Without a scale, a map is simply a diagram or sketch. A map is meaningless without scale.
3. We can measure the distance between two points on the map without actually going to the field.
4. With the help of a scale, the area can be calculated.
5. A certain length can be measured from the linear scale.

Question 5. 
Explain the different methods of showing 
(i) scale on a map. Examine their merits and demerits.   
Answer: 
Scale. Scale is a ratio between map distance and ground distance. The scale may be defined as the ratio which a distance on the map bears to the actual distance on the ground between the same two points.
There are three methods of expressing a scale on map :

1. The statement of the scale.
2. The Representative Fraction (R.F.).
3. The Plain scale or Linear scale or Graphic scale.

All the three types of scales are shown together on a good map.

1. The Statement of the scale. This is the most simple, direct and convenient method of expressing the scale. In this method, the scale is expressed in words. It is stated directly that one inch represents so many miles or one cm represents so many kilometres on the ground. It is written on the map as such :
1 inch: 6 miles
1 cm: 5 km [Note: Use (:) for writing the
5 cms: 1 km Statement. Avoid Writing (=)]

Merits: 

1.  is the brief form of scale.
2. Every layman can understand it.
3. There is no need of calculation. It is clearly known that a unit length on the map represents so much distance on the ground.
4. One can quickly become familiar with this type of scale.

Demerits:

1. This method can be used for only one type of units of measurement.
2. It can be understood by those who are familiar with the unit of measurement used.
3. When a map is reduced or enlarged, the scale will not be the same and the given statement becomes meaningless.
4. Distances cannot be measured from it.

2. The Representative Fraction. When the scale is shown by a fraction, it is known as Representative Fraction. It is usually abbreviated as R.F. R.F. is a fraction whose numerator is always one and shows map distance, while the denominator shows the actual distance on the ground. It is expressed as :

\(\text { R.F. }=\frac{\text { Mapdistance }}{\text { Ground distance }}\)

it can be written as \(\frac{1}{50,000}\) or 1:50,000 or 1/50,000

Example: If a map has a R.F. of 1/50,000, it me answer:one unit on the map represents 50,000 of the same units on the ground. We can say 1 cm on the map represents 50,000 cms on the ground.
Rule :

1. The numerator is always taken as one.
2. Map distance and ground distance should have the same unit of measurement.
3. Because R.F. is a ratio, no unit is written along with it.

Merits :
(i) This scale is independent of any particular unit of measurement. Any unit of measurement whether inches or cms can be used.

(ii) As one unit represents many units, it is known as Representative Fraction.

(iii) It is called a Numerical Scale. It is also known as Natural Scale.

(iv) It is known as international scale as it can be used by any country of the world if a map has a scale of 1" = 1 mile, a Frenchman may not understand it as he is not familiar with the British units. But if this scale is written in the form of R.F. (R. F. = 1/63,360), he will at once understand it. It would mean to him that one cm on the map represents 63,360 cms. on the ground.
(i) R.F. can be converted into statement of scale and vice-versa.

Demerits :

1. Distances cannot be measured on this scale.
2. It needs mathematical calculations and a layman cannot understand it.
3. If a map is photographically enlarged or reduced, the R.F. will not remain true. Plain Scale.

It is also known as a linear scale or graphic scale. In this method, distance is represented graphically along a line. It consists of a straight line drawn at the bottom of the map. It is divided into Primary divisions. The left hand division is sub-divided into Secondary divisions. It has a normal length of 15 cm or 6 inches so that longest measurements can be made on it. It should be geometrically divided and sub¬divided. The units should be shown in round number which is generally a multiple of ten. 

Merits :

1. Direct distances can be measured on this scale. 
2. The distance can be easily measured as there is no need of any calculations.
3. The scale remains true even after the reduction or enlargement of the map by photographic method.
4. It is the basis of scale and it gives a visual impression Conversion of Scale

QUESTION TYPE-I
(To change Statement of Scale into R. F.)

Question 1. 
If the Statement of Scale is 1 cm : 3 km, find out the R.F.
Answer: 
Statement of Scale is 1 cm : 3 km

R.F = \(\frac{\text { Map distance }}{\text { Ground distance }}=\frac{1 \mathrm{~cm}}{3 \mathrm{~km}}\)

= \(\frac{1 \mathrm{~cm}}{3 \times 1,00,000 \mathrm{cms}}\)

[∵ 1 km = 1,00,000cms]
= (Change kms into cms as the unit of measurement should be same on both sides) or 1: 3,00,000.
Note: R.F. is a fraction. No unit of measurement (inch or cm) is written with it.

Question 2. 
If the Statement of Scale is 2 cm : 5 km, find out the R.F.
Answer: 
Statement of Scale is 2 cm : 5 km Map 

\(\text { R.F. }=\frac{\text { Map distance }}{\text { Ground distance }}=\frac{2 \mathrm{~cm}}{5 \mathrm{~km}}\)

 \(=\frac{2 \mathrm{~cm}}{5 \times 1,00,000 \mathrm{cms} .}=\frac{1}{2,50,000}\)

[In R.F., the Numerator (map distance) is always 1], 

Question 3. 
If the Statement of Scale is 1 cm: 50 metres, find out the R.F.
Answer: 
RF = \(\frac{\text { Map distance }}{\text { Ground distance }}=\frac{1 \mathrm{~cm}}{50 \times 1,00 \mathrm{~cm}}\)

[∵ 1 metre = 100 cms]
= \(\frac{1}{5,000}\)or 1:5,000

Question 4. 
If the Statement of Scale is 1 inch: 2 miles, find out the R.F.
Answer: 
Statement of Scale is 1 inch: 2 miles
RF = \(\frac{1 \text { inch }}{2 \text { miles }}=\frac{1 \text { inch }}{2 \times 63,360 \text { inch }}\)
[∵1 mile 63,360 Inches]
[Change miles into Inches]
RF = \(\frac{1}{1,26,720}\) or 1: 1,26,720.

Question 5. 
If the Statement of Scale is 6 inches: 1 mile, find out the R.F.
Answer: 
Statement of Scale is 6": 1 mile
\(\text { R.F. }=\frac{\text { Map distance }}{\text { Ground distance }}\)

\(=\frac{6 \text { inch }}{1 \times 63,360 \text { inches }}\)

\(=\frac{1}{10,560}\) or 1:10,560

Question 6. 
If the Statement of Scale is 1 inch: 500 yards, find out the R.F.
Answer:

\(\text { R.F. }=\frac{\text { Map distance }}{\text { Ground distance }}=\frac{1 \text { inch }}{500 \text { yards }}\)

\(=\frac{1 \text { inch }}{500 \times 36 \text { inches }}\)

[∵ 1 yard = 36 inches]
\(\frac{1}{18,000}\)or 1:18,000
 

QUESTION TYPE-II

(To Change R.F. into Statement of Scale)

Question 7
If R.F of a map is \(\frac{1}{5,00,000}\) find out the statement of scale in kilometers.
Answer:
\(\text { R.F. }=\frac{\text { Map distance }}{\text { Ground distance }}=\frac{1}{5,00,000}\)
∴ 1 cm : 5,00,000 cms
[∵ the basic unit of kms is cm]
1 cm: \(\frac{5,00,000}{1,00,000}\)kms
[∴ 1km = 1,00,000cm]
= 5 kms
So the Statement of Scale is 1 cm: 5 km.

Question 8. 
Answer:
R.F  \(=\frac{\text { Map distance }}{\text { Ground distance }}\)
1 inch : 1,90,080 inches
[∵ the basic unit of miles is inch]
\(1 \text { inch }: \frac{1,90,080}{63,360} \text { miles }\)

[∵ 1 mile = 63,360 inches]
= 3 miles
so the statement of scale is 1 inch : 3 miles

Question 9. 
If R.F. of a map is 1/7200, find out the Statement of Scale in yards.
Answer:
RF = \(\frac{\text { Map distance }}{\text { Ground distance }}=\frac{1}{7200}\)

1 inch : 7200 inch 
:\(\frac{7200}{36}\)yards 
[∴ 1 yard = 36 inches]
200 yards
so the statement of scale is 1 inch : 200 yards.

Question 10. 
If R.F. of a map is 1/1,000,000 find out the Statement of Scale both in miles and kilometres. 
Answer: 
(i) In miles-
\(\text { R.F. }=\frac{\text { Map distance }}{\text { Ground distance }}=\frac{1}{1,000,000}\)

1 inch : 1,00,000 inches

\(: \frac{1,000,000}{63,360} \text { miles }\)

∴1 mile = 63,360 inchesj
: 15.78 miles approximately
So the Statement of Scale is 1 inch : 15.78 miles.

(ii) In kilometres-
R.F = \(\frac{1}{1,00,000}\)(1 km : 1,00,000 cms)
1 cm : \(\frac{1,000,000}{1,00,000}\)kms = 10 kms
so the statement of scale is 1cm : 10 kms

QUESTION TYPE-III

(To Find out Actual distance and R.F.)

Question 11. 
The actual distance between two places is 40 kms. It is shown by a distance of 5 cms on the map. Find out the R.F. of the map.
Answer:
5 cms on the map represents on the ground = 40 km. 1 cm on the map represents on the ground

\(=\frac{40 \times 1,00,000}{5} \mathrm{cms}\)

= 8,00,000 cms

\(\therefore \quad \text { R.F. }=\frac{1}{8,000,00}\)

or on other way:

\(\text { R.F. }=\frac{\text { Map distance }}{\text { Ground distance }}\)

\(=\frac{5 \mathrm{cms}}{40,00,000 \mathrm{cms}}=\frac{1}{8,000,00}\)

Rules :

1. In R.F., the numerator is always 1.
2. The unit of measurement for the numerator and the Denominator must be the same.

Question 12. 
The distance between two places is 5 cms on the map. The R.F. of the map is 1/200,000. Find out the actual distance between the two places on the ground.

\(\text { R.F. }=\frac{1}{2,00,000}\)

One cm. on the map represents on the ground
= 2,00,000 cms.
5 cms. on the map represents on the ground

\(=\frac{2,00,000 \times 5}{1,00,000} \mathrm{kms}=10 \mathrm{kms}\)

QUESTION TYPE-IV

(Drawing of a Linear Scale or Plain Scale) In this method, map distance is shown by a straight line drawn at the bottom of the map. This straight line is divided into a number of equal primary divisions. Each primary division is subdivided into equal secondary divisions. To divide a line into equal parts. First Method. Suppose we have to divide a straight line AB into five equal parts. Draw another line OA making a convenient acute angle L OAB. On line

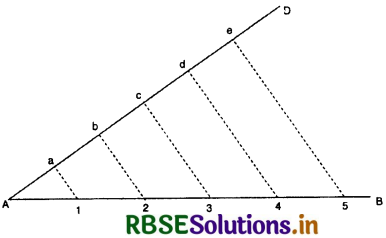
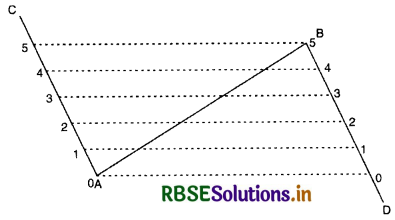
AO mark off five equal divisions (a, b, c, d, and e). Join the last point e and B. From points a , b, c, d draw lines parallel to eB with the help of a set square. These parallel lines cut AB into five equal divisions. Second Method. Suppose we have to divide a line AB into five equal parts. Draw angle of 90° (in opposite directions) at both ends A and B of the straight line AB. Mark off five equal divisions (1, 2, 3, 4, 5) from A towards AC. Similarly, mark off five equal divisions (1, 2, 3, 4, 5) from B towards BD. As shown in the diagram, join these divisions to draw parallel lines. These parallel lines will cut AB into five equal parts.

Precautions :
1. Length of the Scale. The normal length of the plain scale should be about 6 inch or 15 cm. It is a convenient and useful length which can be divided and subdivided into Primary and Secondary divisions.

2. Round Number. The plain scale should show the distance in round number in kms or miles. It should
be in multiples of ten (10, 20, 30, 40  ), So that secondary divisions are possible

3. Primary and Secondary Divisions. The plain scale should be divided into primary divisions and sub-divided into secondary divisions.

4. Statement of Scale and R.F. The Statement of Scale should be written above the plain scale while R.F. should be written below the plain scale.

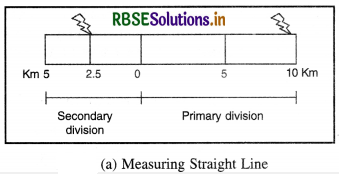
5. Zero of the Scale. Zero should be marked after one division from the left of the scale. The divisions to the right of the zero show primary divisions while the divisions to the left of the zero are shown as secondary divisions.

6. Unit of Measurement. The distance should be written in numbers and the units of measurement should be written in letters like “KILOMETRES” or “MILES”.

7. Shading. Each plain scale should be subdivided into two equal parts and it should be shaded alternately.
 
QUESTION TYPE-V

(To draw a plain scale when the Statement of Scale is given)

Question 13. 
Draw a plain scale for a map whose scale is 1 cm: 10 km.
Answer: 
1 cm on the map represents on the ground
= 10 km
15 cm on the map represents on the ground
= 10 x 15 = 150 km.
(The Normal length of scale should be 15 cm)
150 km is a round number Therefore, we need not select any other number.

Construction. Draw a line 15 cm. long. Divide it into 15 primary divisions. Each division represents 10 km. Sub-divide the left hand division into five secondary divisions, each showing a distance of 2 kms. 

Question 14. 
Draw a plain scale for a map whose scale- is 1 cm: 7 km
Answer:
Scale is 1 cm: 7 km.
1 cm on the map represents on the ground
=7km
15 cm on the map represents on the ground
= 7 X 15 = 105 km.
Let us take a convenient round number of loo kilometres.
Find out the map distance for a distance of 100 kms.
7 kms are shown on the map = 1 cm
1 km = is shown on the map = \(\frac{1}{7}\)cm
100 kms are shoen on the map = \(\frac{100}{7}\)cm =14.3 cm



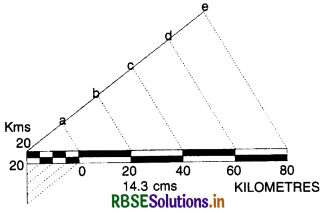
Construction. Draw a line 14.3 cm long. Divide it into five equal parts. Each part will show 20 kms. Sub-divide the left hand division into four equal parts, each part will show a distance of 5 kms.

Question 15. 
Draw a plain scale for a map whose scale is 1 inch: 7 miles.
Answer: 
1 inch represents a distance = 7 miles
6 inch represents a distance = 7 x 6 = 42 miles
But 42 miles is not a round number. Select a round number of 45 miles. Find out the map distance for a distance of 45 miles.
7 miles are represented by= 1 inch
1 mile is represented by = \(\frac{1}{7}\) inch 45 miles are represented by = \(\frac{1}{7}\) x 45 = 6.4 inch approximately



Construction. Draw a line 6.4 inches long. Divide it into nine equal parts, each part showing 5 miles. Sub-divide the left-hand part into 5 divisions, each will show a distance of 1 mile.

QUESTION TYPE-VI

To draw a plain scale when R. F. is given)

Question 16. 
Draw a plain scale to show kilometres for a map whose RF is \(\frac{1}{100,000}\)
Answer: 
 RF = \(\frac{1}{100,000}\)
1 cm on the map shows on the ground
= 100,000 cms.
= 1 km.
15 cm on the map shows on the ground = 15 km.

 

Construction. Draw a line 15 cm. long. Divide it into 5 equal parts each showing 3 kms. Sub-divide the left-hand part into 3 divisions. Each will show 1 km.

Question 17. 
Draw a plain scale to show kilometres and metres for a map whose R.F. is 1/50,000. Show a distance of 4 kms. and 600 metres on the scale
Answer: 

\(\text { R.F. }=\frac{1}{50,000}\)

1 cm on the map shows = 50,000 cms.

\(=\frac{50,000}{1,00,000} \mathrm{kms.}=\frac{1}{2} \mathrm{~km}\)

16 cm on the map shows \(\frac{16}{2}\)= 8 km 

Construction. Draw a line 16 cm long. Divide it into 8 equal parts, each part will show 1 km. Sub-divide the left hand part into 5 equal divisions each showing 200 metres. The distance of 4 km and 600 metres on the scale
= 4 km + 600 metres
=4 primary divisions +3 Secondary divisions
This distance can be shown on the scale by marking arrows.

Question 18. 
The actual distance between Amritsar and Jalandhar is 78 km. It is shown by a distance of 5.2 cm on the map. Find out the scale of map.
Answer: 
\(\frac{52}{10}\)cms on the map show a distance = 78 kms
1 cm on the map shows a distance = \(\frac{78 \times 10}{52}\)

= 15 kms.
So the statement of scale is 1 cm: 15 kms.

Question 19.
Draw a plain scale to show miles for a map whose R.F. is \(\frac{1}{1,000,000}\)
Answer: 
R.F. = 1: 1,000,000
∴ one inch on the map represents = 1,000,000
inches = \(\frac{1,000,000}{63,360}\)miles
6 inches on the map represents
 \(=\frac{1,000,000}{63,360}\)x 6 miles
\(=\frac{1,000,000}{1056}=\frac{12500}{132} \text { miles }=\frac{3125}{33} \text { miles }\)
= 94.69 miles approximately 
But \(\frac{3125}{33}\)or 94.69 miles is not a round number.
Select a Round number of 100 miles.
\(\frac{1,000,000}{63,360}\)miles are shown by = 1 inch
1 mile is shown by = \(\frac{1 \times 63360}{1,000,000}\)inches
100 miles are shown by = \(\frac{100 \times 63360}{1,000,000}\) inches
= \(\frac{6336}{1000}\)inches = 6.336 inches
= 6.3 inches approximately.

Construction. Draw a line 6.3 inches long. Divide it into 10 equal parts each showing 10 miles. Subdivide the left hand part into 5 divisions; each will show 2 miles.

Question 20.
Describe the different methods of. measuring distances on a map. :
Answer: 
Linear distances on maps are of two types:
(1) Straight lines: like roads, railway lines, and canals.

(2) Curved or zigzag line: like streams, Coastlines etc.

(A) Straight lines distance. When the line is straight the distance can be measured with the help of a divider. Place the divider on calibrated bar scale to get the distance on the ground.

(B) Curved Lines: When the route is zigzag, place one end of a thread at the starting point and carry the thread along the line. After completing the distance stretch the thread and measure the length. It will give approximate distance as depicted O (b).

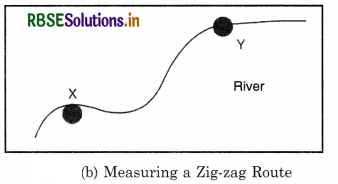
It can also be measured with the help of a plain divider, as explained earlier, but the measurement will be less accurate. It can also be done with the help of a strip of paper.

(e) Rotameter is an instrument having a route measuring wheel. Distance between two points is measured by allowing the wheel of the rotameter to move along the route.

QUESTIONS FOR VIVA-VOCE 

Question 1. 
How many inches are there in one mile? 
Answer: 
63,360.

Question 2. 
How many centimetres are there in one km?
Answer: 
One lakh (1,00,000).

Question 3. 
Name the methods of showing scale. 
Answer: 

1. Statement of scale 
2. R.F. (i) Plain scale, (g) 

Question 4. 
Name the different types of Plain Scale.- 
Answer: 

1. Linear scale 
2. Comparative scale 
3. Scale of paces 
4. Time scale. (g) 

Question 5. 
State the rule to find out R.F.
Answer: 
R.F. = Map distance / Ground distance.

Question 6. 
What is the standard length of a scale? 
Answer: 
15 centimetres or 6 inches.

Question 7. 
If the statement of scale is 1:1 yard, find out R.F.
Answer: 
R.F. = 1/36 (1 yard = 3 x 12 = 36 inches).
 
Question 8. 
If the R.F. of a map is 1/1,00,000, state the ;
statement of scale (in kms).
Answer: 
1 cm: 1 kilometre.

Question 9. 
If the statement of scale is 1:1 mile, state the R.F.
Answer: 
R.F. = 1/63,360.

Question 10. 
Where does zero start on a plain scale?
Answer: 
After leaving the left-hand primary division. 

Question 11. 
What is meant by 1 and 100 in an R.F. of 1/100? 
Answer: 
1 is the numerator and is map distance while 100 is the denominator and is ground distance.

Question 12. 
What other names are given to R.F.?
Answer: 
Numerical scale and international scale.

Question 13. 
Why is R.F. called Representative Fraction?
Answer: 
Because one unit of the numerator represents other units of the denominator.

Question 14. 
What is the abbreviation of Representative Fraction?
Answer: 
R.F.