RBSE Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Exercise 9.4

Question 1.
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Answer:
Given: A ||gm ABCD and a rectangle ABEF with same base AB and equal areas.
To show: Perimeter of ||gm ABCD > Perimeter of rectangle ABEF.

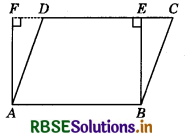
Since, opposite sides of a ||gm and rectangle are equal, therefore
AB = DC (∵ ABCD is a ||gm)
and, AB = EF (∵ABEF is a rectangle)
∴ DC = EF .......... (1)
∴ AB + DC = AB + EF ............ (2)
Since, all the segments that can be drawn to a given line from a point not lying on it, the perpendicular segment is the shortest, therefore
BE < BC and AF < AD
So, BC > BE and AD > AF
∴ BC + AD > BE + AF
Adding (2) and (3), we get ............. (3)
AB + DC + BC + AD > AB + EF + BE + AF
or AB + BC + CD + DA > AB + BE + EF + FA
Hence, perimeter of ||gm ABCD > perimeter of rectangle ABEF.
Hence proved.

Question 2.
In the figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (ABC).
(Remark : Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC you can divide AABC into n triangles of equal areas.)

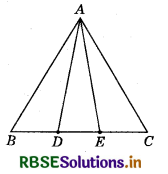
Answer:
Given : BD = DE
∴ AD is the median of ∆ABE
∴ ar∆ABD = ar∆ADB .............. (1)
(Median divides the triangle in two triangles of equal area.)
Since, DE = EC in ∆ADC
ar∆ADB = ar∆AEC .......... (2)
(Median divides the triangle in two triangles of equal area.)
from (1) and (2) we get
ar∆ABD = ar∆AEC
(Two things equal to the same thing are equal to each other.)
Hence, ar ∆ABD = ar ∆AEC = ar ∆ADE
Hence proved.

Question 3.
In the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

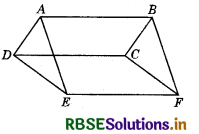
Answer:
Since, opposite sides of a ||gm are equal.
AD = BC (∵ ABCD is a ||gm)
DE = CF (∵ DCFE is a ||gm)
and AB = BF (∵ ABFE is a ||gm)
Consider ∆s ADE and BCF, in which AB = BF, AD = BC and DE = CF
∴ By SSS criterion of congruence, we have:
∆ADE ≅ ABCF
So, ar (ADE) = ar (BCF).
Hence Proved

Question 4.
In the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
(Hint : Join AC.)

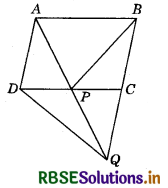
Answer:
Join AC.
Since, As APC and BPC are on the same base PC and between the same parallels PC and AB, therefore
ar (APO = ar (BPC) .......... (1)
Now, AD = CQ
and AD || CQ (Given)

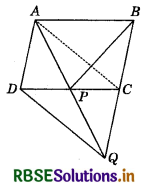
∴ In the quadrilateral ADQC, one pair of opposite sides is equal and parallel.
∴ ADQC is a parallelogram.
So, AP = PQ and CP = DP
(∵ Diagonals of a ||gm bisect each other)
In ∆s APC and DPQ, we have :
AP = PQ
∠APC = ∠DPQ
and PC = PD
∴ By SAS criterion of congruence,
∆APC ≅ ∆DPQ
∴ ar (APC) = ar (DPQ) ........... (2) [∵ Congruent ∆s have equal area]
∴ ar (BPQ = ar (DPQ) [From (1) and (2)]
Hence Proved.

Question 5.
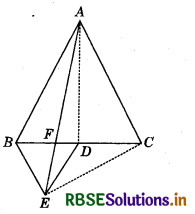
In the figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:

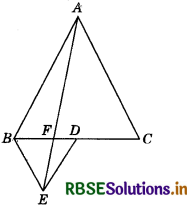
(i) ar (BDE) = \(\frac{1}{4}\) ar (ABC)
(ii) ar (BDE) = \(\frac{1}{2}\)ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = \(\frac{1}{8}\)ar (AFC).
[Hint s Join EC and AD. Show that BE || AC and DE || AB, etc.]
Answer:
Join EC and AD. Let a be the side of ∆ ABC.
Then, ar (ABC) = \(\frac{\sqrt{3}}{4}\) a² = ∆ (say)

(i) ar(ABC) = \(\frac{\sqrt{3}}{4}\left(\frac{a}{2}\right)^{2}\) [∵ BD = \(\frac{1}{2}\)BC = \(\frac{a}{2}\)
= \(\frac{\sqrt{3}}{16} a^{2}=\frac{\Delta}{4}\)
or ar(BDE) = \(\frac{1}{4}\)ar (ABC)

(ii) We have: ar (BDE) = \(\frac{1}{2}\)ar (BEC) ......... (1)

(∵ DE is a median of ∆ BEC and each median divides a triangle into two ∆ s of equal area.)
Now, ∠EBC = 60°
and ∠BCA = 60°
So, ∠EBC = ∠BCA.
But these are alternate angles with respect to the line-segments BE and CA and their transversal BC.
Hence, BE || AC
Now, ∆s BEC and BAE stand on the same base BE and lie between the same parallels BE and AC.
∴ ar (BEC) = ar (BAE)
∴ From (1), ar (∆BDE) = \(\frac{1}{2}\)ar (BAE).

(iii) Since ED is a median of ∆BEC and we know that each median divides a ∆s of equal area, therefore
ar (BDE) = \(\frac{1}{2}\)ar (BEC)
From part (i) ar (BDE) = \(\frac{1}{4}\)ar (ABC)
Combining these results, we get:
\(\frac{1}{4}\)ar (ABC) = \(\frac{1}{2}\)ar (BEC)
⇒ ar (ABC) = 2ar (BEC)

(iv) Now, ∠ABD = ∠BDE = 60° (given)
But ∠ABD and ∠BDE are alternate angles with respect to the line-segment BA and DE and their transversal BD.
Hence BA || ED:
Now, ∆s BDE and AED stand on the same base ED and lie between the same parallels BA and DE.
∴ ar (BDE) = ar (AED)
So, ar (BDE) - ar (FED) = ar (AED) - ar (FED)
∴ ar (BEF) = ar (AFD)

(v)


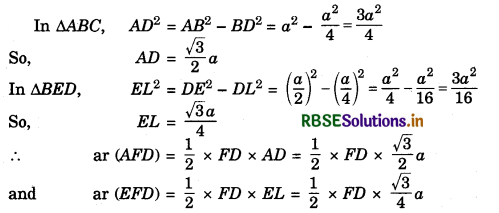
From (1) and (2), we have ar (AFD) = 2 ar (EFD)
Combining this result with part (iv),
we have : ar (BFE) = ar (AFD) = 2ar (EFD)

(vi) From part (i), ar (BDE) = \(\frac{1}{4}\) ar (ABC)
So, ar (BEF) + ar (FED) = \(\frac{1}{2}\) × 2ar (ADC)
or 2ar (FED) + ar (FED) = \(\frac{1}{2}\) [ar (AFC) - ar (AFD)] [Using part (v)]
So, 3ar (FED) = \(\frac{1}{2}\) ar (AFC) - \(\frac{1}{2}\) × 2 ar (FED)
or 4ar (FED) = \(\frac{1}{2}\)ar (AFC)
⇒ ar (FFD) = \(\frac{1}{8}\)ar (AFC).

Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[Hint: From A and C, draw perpendiculars to BD.]
Answer:

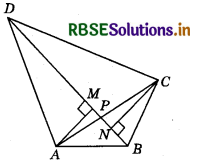
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P.
Draw AM ⊥ BD and CN ⊥ BD.
Now, ar (APB) × ar (CPD) = (\(\frac{1}{2}\) × BP × AM) × (\(\frac{1}{2}\) × DP × CN)
= \(\frac{1}{4}\) × BP × DP × AM × CN ............ (1)
and, ar (APD) × ar (BPC) = (\(\frac{1}{2}\) × DP × AM) × (\(\frac{1}{2}\) × BP × CN)
= \(\frac{1}{4}\) × BP × DP × AM × CN ............. (2)
From (1) and (2), we have :
ar (APB) × ar (CPD) = ar (APD) × ar (BPC).

Question 7.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP. Show that:
(i) ar (PRQ) = \(\frac{1}{2}\)ar (ARC)
(ii) ar (RQC) = \(\frac{3}{8}\)ar (ABC)
(iii) ar (PBQ) = ar (ARC).
Answer:

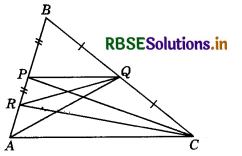
P and Q are respectively the mid-points of sides AB and BC of ∆ABC and R is the mid-point of AP.
Join AQ and PC.

(i) We have : ar (PQR) = \(\frac{1}{2}\)ar (APQ)
(∵ QR is a median of ∆APQ and it divides the ∆ into two ∆s of equal area.)
= \(\frac{1}{2}\) × \(\frac{1}{2}\) ar (ABQ) (∵ QP is a median of ∆ABQ)
= \(\frac{1}{4}\)ar (ABQ) = \(\frac{1}{4}\)× \(\frac{1}{2}\)ar (ABC) (∵ AQ is a median of ∆ABQ) ......... (1)
= \(\frac{1}{8}\)ar (ABC)  .............. (1)
Again, ar(ARC) = \(\frac{1}{2}\)ar (APC) (∵ CR is a median of ∆APC)
= \(\frac{1}{2}\) × \(\frac{1}{2}\)ar (ABC) (∵ CP is a median of ∆ABC.) ................ (2)
=  \(\frac{1}{4}\)ar (ABC)
From (1) and (2), we get:
ar (PQR) = \(\frac{1}{8}\)ar (ABC) = \(\frac{1}{2}\) × \(\frac{1}{4}\)ar (ABC) = \(\frac{1}{2}\)ar (ARC)

(ii) We have: ar (RQA) + ar(AQC) - ar (ARC) .................. (3)

Question 8.
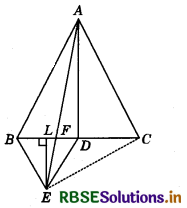
In the figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:

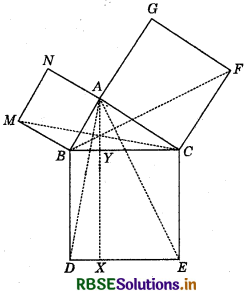
(i) ∆MBC ≅ ∆ABD 
(ii) ar (BYXD) = 2 ar (MBC)
(iii)    ar (BYXD) = ar (ABMN)
(iv)    ∆FCB ≅ ∆ACE
(v)    ar (CYXE) = 2 ar (FCB)
(vi)    ar (CYXE) = ar (ACFG)
(vii)    ar (BCED) = ar (ABMN) + ar (ACFG)
Note: Result (vii) is the famous Theorem pf Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Answer:
(i) In As MBC and ABD, we have:
BC = BD (Sides of the square BCED)