RBSE Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.3

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.3 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 9 Areas of Parallelograms and Triangles Exercise 9.3

Question 1.
In the figure, E is any point on median AD of a ∆ABC. Show that ar (ABE) = ar (ACE).

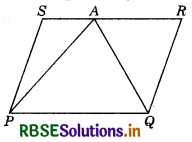
Answer:
Given: AD is a median of ∆ABC and E is any point on AD.
To show: ar (ABE) = ar (ACE).
∵ AD is the median of ∆ABC
∴ ar (ABD) = ar (ACD) ............ (1)
Also, ED is the median of ∆EBC
ar (BED) = ar (CED)
Subtracting (2) from (1), we get ........... (2)
ar (ABD) - ar (BED) = ar (ACD) - ar (CED)
or ar (ABE) = ar (ACE).
Hence proved.

Question 2.
In a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = \(\frac{1}{4}\) ar (ABC).
Answer:
Given: In ∆ABC, E is the mid-point of the median AD.
To show: ar(BED) = \(\frac{1}{2}\) ar (ABC).
Since AD is a median of ∆ABC and median divides a triangle into two triangles of equal area, therefore
ar (ABD) = \(\frac{1}{2}\)ar (ADC)
or ar (ABD) = \(\frac{1}{2}\)ar (ABC) ....... (1)
In ∆ABD, BE is the median.
∴ ar (BED) = ar (BAE) ............ (2)
or ar (BED) = ∴ ar (ABD)
So, ar (BED) = \(\frac{1}{2}\) × \(\frac{1}{2}\)ar (ABC) [Using (1)]
ar (BED) = \(\frac{1}{4}\)ar (ABC).
Hence proved.

Question 3.
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer:

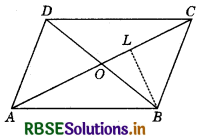
Given A parallelogram ABCD.
To show: The diagonals AC and BD divide the ||gm ABCD into four triangles of equal area.
Construction : Draw BL ⊥ AC.
Since, ABCD is a ||gm and so its diagonals AC and BD bisect each other at O.
∴ AO = OC and BO = OD
Now, ar (AOB) = \(\frac{1}{2}\) × AO × BL
and ar (OBC) = \(\frac{1}{2}\) × OC × BL
But AO = OC.
∴ ar (AOB) = ar (OBC)
Similarly, we can show that
ar (OBC) = ar (OCD); ar (OCD) = ar (ODA).
ar (ODA) = ar (OAB); ar (OAB) = ar (OBC)
and ar (OCD) = ar (ODA)
Thus, ar (OAB) = ar (OBC)
= ar (OCD) = ar (OAD)
Hence Proved.

Question 4.
In the figure, ABC and ABD are two triangles on the same hase AB. If line segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).

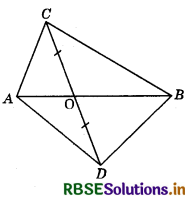
Answer:
Given : ABC and ABD are two triangles on the same base AB. The line segment CD is bisected by AB at O i.e., OC = OD.
To show : ar (ABC) = ar (ABD).
In AACD, we have :
OC = OD (Given)
∴ AO is the median.
∴ ar (AOQ = ar (AOD) ........... (1)
(∵ Median divides a ∆ in two ∆s of equal area)
Similarly, in ABCD, BO is the median.
∴ ar (BOC) = ar (BOD) ............ (2)
Adding (1) and (2), we get
ar (AOO + ar (BOO = ar (AOD) + ar (BOD)
⇒ ar (ABC) = ar (ABD).
Hence Proved.

Question 5.
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ∆ABC. Show that:
(i) BDEF is a parallelogram
(ii) ar (DEF) = \(\frac{1}{4}\)ar (ABC)
(iii) ar (BDEF) = \(\frac{1}{2}\) ar (ABC).
Answer:

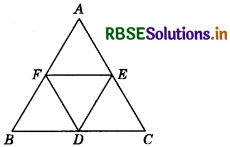
Given: D, E and F are the mid-points of the sides BC, CA and AB respectively of ∆ABC.
To show:
(i) BDEF is a ||gm
(ii) ar (DEF) = \(\frac{1}{4}\)ar (ABC)
(iii) ar (BDEF) = \(\frac{1}{2}\)ar (ABC)

(i) We have in ∆ABC,
EF || BC
(By mid-point theorem, since E and F are the mid-points of AC and AB respectively)
∴ EF || BD ........ (1)
Also, ED || AB
(By mid-point theorem, since E and D are the mid-points of AC and BC respectively)
∴ ED || AF ......... (2)
From (1) and (2), BDEF is a ||gm.

(ii) Similarly, FDCE and AFDE are also ||gms.
∴ ar (FBD) = ar (DEF) (∵FD is a diagonal of ||gm BDEF)
ar (DEC) = ar (DEF) (∵ ED is a diagonal of ||gm FDCE)
and ar (AFE) = ar (DEF) (∵ FE is a diagonal of ||gm AFDE)
∴ ar (FBD) = ar (DEC) = ar (AFE) = ar (DEF)
⇒ ar (DEF) = \(\frac{1}{4}\)ar (ABC).

(iii) Also, ar (BDEF) = 2 ar (DEF)
= 2 × \(\frac{1}{4}\)ar (ABC) = \(\frac{1}{2}\)ar (ABC).
Hence Proved.

Question 6.
In the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB or ABCD is a parallelogram.
(Hint: From D and B, draw perpendiculars to AC.)

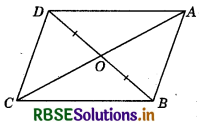
Answer:

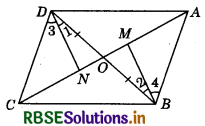
(i) Draw DN ⊥ AC and BM ⊥ AC.
In ∆s DON and BOM, we have :
∠DNO = ∠BMO (Each = 90°)
∠DON = ∠BOM (Vert. opp. ∠s)
OD = OB (Given)
By AAS criterion of congruence,
∆DON = ∆BOM
In ∆s DCN and BAM,
∠DNC = ∠BMA
DC = AB
DN = BM (∵ ∆DON ≅ ∆BOM ⇒ DN = BM)
∴ By RHS criterion of congruence,
∆DCN ≅ ∆BAM
From (1) and (2), we get
ar (DON) + ar (DCN) = ar (BOM) + ar (BAM)
So, ar (DOC) = ar (AOB)

(ii) Since ar (DOC) = ar (AOB)
therefore ar (DOC) + ar (BOC) = ar (AOB) + ar (BOC)
or ar (DCB) = ar (ACE)

(iii) ∆s DCB and ACB have equal areas and have the same base. So, these As must lie between the same parallels.
So, DA || CB.
Now, from (1), ∠1 = ∠2 (CPCT) (3)
and from (2), ∠3 = ∠4 (CPCT) (4)
So, ∠1 + ∠3 = ∠2 + ∠4 [From (3) and (4)]
So, ∠CDB = ∠ADB
∴ CD||AB (Alternate angles)
∴ ABCD is a parallelogram. (Opposite sides are parallel.)
Hence proved.

Question 7.
D and E are points on sides AB and AC respectively of ∆ABC such that ar (DBC) = ar (EBC). Prove that DE || BC.
Answer:

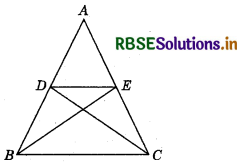
Since ∆s DBC and EBC are equal in area and have a same base BC, therefore.
Altitude from D of ∆DBC = altitude from E of ∆EBC.
So, ∆s DBC and EBC are between the same parallels. i.e. DE || BC.
Hence proved.

Question 8.
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar (ABE) = ar (ACF).
Answer:

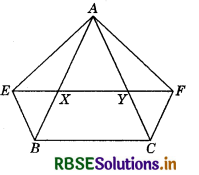
Here, XY || BC and BE || CY.
∵ BCYE is a ]|gm.
Since ∆ABE and ||gm BCYE are on the same base BE and between the same parallels BE and AC, therefore
(ABE) = \(\frac{1}{2}\)ar (BCYE)
Now, CF || AB and XY || BC
So, CF || AB and XF || BC
∴ BCFX is a ||gm.
Since ∆ACF and ||gm BCFX are on the same base CF and between the same parallels AB and FC, therefore
ar (ACF) = \(\frac{1}{2}\)ar (BCFX ......... (2)
But ||gm BCFX and ||gm BCYE are on the same base BC and between the same parallels BC and EF
∴ ar (BCFX) = ar (BCYE) ........... (3)
From (1), (2) and (3), we get :
ar (∆ABE) = ar (∆ACF).
Hence Proved.

Question 9.
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see figure). Show that ar (ABCD) = ar (PBQR).
[Hint : Join AC and PQ. Now compare ar (ACQ) and ar (APQ).]

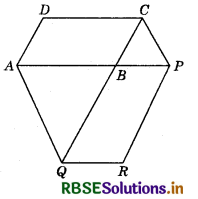
Answer:
Join AC and PQ. Since AC and PQ are diagonals of ||gm ABCD and ||gm PBQR respectively.
Therefore,
ar (ABC) = \(\frac{1}{2}\)ar (ABCD) ............. (1)
and ar(PBQ) = \(\frac{1}{2}\)ar(PBQR) .............. (2)
Now, ∆s ACQ and AQP are on the same base AQ and the same parallels AQ and CP.

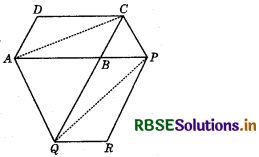
∴ ar (ACQ) = ar (AQP)
So, ar (ACQ) - ar (ABQ) = ar (AQP) - ar (ABQ) [Subtracting ar (ABQ) from both sides]
⇒ ar (ABC) = ar (BPQ)
⇒ \(\frac{1}{2}\)ar (ABCD) = \(\frac{1}{2}\)ar (PBQR) [Using (1) and (2)]
⇒ ar (ABCD) = ar (PBQR).
Hence Proved.

Question 10.
Diagonals AC and BD of a trapezium ABCD with AB other at O. Prove that ar (AOD) = ar (BOC).
Answer:

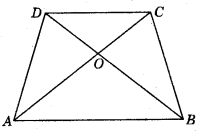
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O.
∴ ∆s ABC and ABD are on the same base and between the same parallels.
∴ ar (ABD) = ar (ABC)
So, ar (ABD) - ar (AOB) = ar (ABC) - ar (AOB)
[Subtracting ar (AOB) from both sides]
∴ ar (AOD) = ar (BOC).
Hence Proved.

Question 11.
In the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE).
Answer:

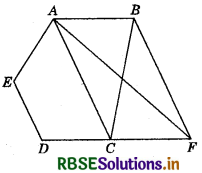
(i) Since, As ACB and ACF are on the same base AC and between the same parallels AC and BF, therefore
ar (ACB) = ar (ACF).

(ii) Adding ar (ACDE) on both sides, we get
ar (ACF) + ar (ACDE) = ar (ACB) + ar (ACDE)
i.e. ar (AEDF) = ar (ABCDE).
Hence proved.

Question 12.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Answer:

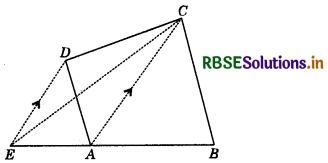
Let ABCD be the quadrilateral plot. Produce BA to meet DE drawn parallel to CA at E. Join EC.
Then, ∆s EAC and ADC lie on the same base AC and same parallels DE and CA
ar (EAC) = ar (ADO
Now ar (ABCD) = ar (ABO + ar (ACD)
= ar (ABC) + ar (EAC) = ar (EBC)
i.e. ar (ABCD) = ar (EDC)
which is the required explanation to the suggested proposal.

Question 13.
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACT).
[Hint: Join CX]
Answer:

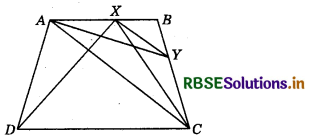
ABCD is a trapezium with AB || DC and XY. || AC is drawn. Join XC and XD.
ar (ACX) = ar (ACY) .......... (1)
(∵ ∆s ACX and ACY have same base AC and are between same parallels AC and XY.)
But ar (ACX) = ar (ADX) .......... (2)
(∵ ∆s ACX and ADX have same base AX and are between same parallels AB and DC.)
From (1) and (2), we have ar (ADX) = ar (ACY).

Question 14.
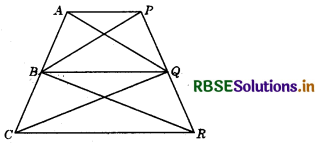
In the figure, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).

Answer:
From the figure, we have :
ar (AQC) = ar (AQB) + ar (BQC) ......... (1)
and, ar (PBR) = ar (PBQ) + ar (QBR) .......... (2)
But ar (AQB) = ar (PBQ) ........ (3)
(∵ These ∆s are on the same base BQ and between same parallel lines AP and BQ.)
Also, ar (BQQ = ar (QBR) ............ (4)
(∵ These As are on the same base BQ and between same parallel lines BQ and CR)
Using (3) and (4) in (1) and (2), we get:
ar (AQC) = ar (PBR).
Hence proved.

Question 15.
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOO. Prove that ABCD is a trapezium.
Answer:

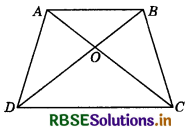
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that
ar (AOD) = ar (BOC) ............ (1)
Adding ar (ODC) on both sides, we get
ar (AOD) + ar (ODO = ar (BOO + ar (ODO D
or ar (ADC) = ar (BDC)
As ∆ADC and ∆BDC are on the same base DC and having the same areas, therefore they must lie between the same parallels.
So, AB || DC.
Hence, ABCD is a trapezium.
Hence Proved.

Question 16.
In the figure, ar (DRC) = ar (DPO and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

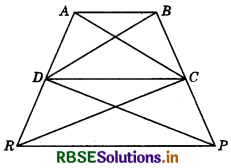
Answer:
From the figure,
ar (BDP) = ar (ARC) (Given)
and ar (DPC) = ar (DRC) (Given)
On subtracting, we get
ar (BDP) - ar (DPC) = ar (ARC) - ar (DRC)
So ar (BDC) = ar (ADC)
These two triangles are on the same base DC.
∴ DC || AB
(The two triangles must lie between the same parallels)
Hence, ABCD is a trapezium.
Also ar (DRC) = ar (DPC) (Given)
These two triangles have the same base DC.
So RP || DC
(They must lie between the same parallels)
Hence, DCPR is a trapezium.
Hence proved.