RBSE Solutions for Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Ex 9.2

प्रश्न 1.
आकृति में, ABCD एक समान्तर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।

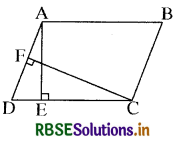
हल:
प्रश्नानुसार दिए गए समान्तर चतुर्भुज में आमने-सामने की भुजाएँ बराबर होती हैं अतः
AB = DC = 16 cm
तथा AE ⊥ DC (दिया है)

समान्तर चतुर्भुज ABCD का क्षेत्रफल
= DC × AE
या ar (∥ gm) = आधार × संगत ऊँचाई
= 16 cm. × 8 cm.
= 128 cm²

अब आधार AD तथा ऊँचाई CF के अनुसार समान्तर चतुर्भुज का क्षेत्रफल
= AD × CF

या 128 cm = AD × 10 cm.
या AD × 10 cm² = 128 cm²
या AD = \(\frac{1.28}{10}\) cm.
AD = 12.8 cm.

प्रश्न 2.
यदि E, F, G और H क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं के मध्य-बिन्दु हैं, तो दर्शाइए कि ar (EFGH) = \frac{1}{2}ar (ABCD) है।
हल:
दिया है-एक समान्तर चतुर्भुज ABCD है जिसमें भुजाओं AB, BC, CD और DA के मध्य
बिन्दु क्रमशः E, F, G और H हैं।

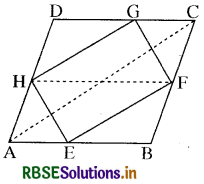
सिद्ध करना है
ar (EFGH) = \(\frac{1}{2}\)ar (ABCD)

रचना - समान्तर चतुर्भुज के बिन्दु A व C तथा H व F को मिलाया।
उपपत्ति - चित्रानुसार ∆ABC में भुजा AB का मध्य-बिन्दु E तथा भुजा BC का मध्य-बिन्दु F है।
∴ EF = \(\frac{1}{2}\)AC
तथा EF ∥ AC .....(i)

इसी प्रकार ∆ADC में भुजा DC तथा AD के मध्य बिन्दु क्रमशः G व H हैं।
∴ GH = \(\frac{1}{2}\)AC
तथा GH ∥ AC .....(ii)

समीकरण (i) व (ii) से
GH = EF तथा GH ∥ EF
अतः चतुर्भुज EFGH एक समान्तर चतुर्भुज है क्योंकि यदि चतुर्भुज की सम्मुख भुजाओं का एक युग्म समान एवं समान्तर हो तो यह समान्तर चतुर्भुज होता है। अब समान्तर चतुर्भुज ABCD में
AD = BC

तथा AD ∥ BC (क्योंकि ये समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं)
∴ \(\frac{1}{2}\)AD = \(\frac{1}{2}\)BC
तथा AD ∥ BC
या HD = FC
तथा HD ∥ FC
अत: HDFC एक समान्तर चतुर्भुज है।

हम जानते हैं कि ∆HGF और समान्तर चतुर्भुज HDFC एक ही आधार HF तथा एक ही समान्तर रेखाओं के बीच स्थित हैं।
अतः ar (∆HGF) = \(\frac{1}{2}\)ar(समान्तर चतुर्भुज HDFC) .....(iii)

इसी प्रकार हम सिद्ध कर सकते हैं कि
ar (∆HEF) = \(\frac{1}{2}\)ar(समान्तर चतुर्भुज HABF) ...(iv)

समीकरण (iii) व (iv) को जोड़ने पर
ar (∆HGF) + ar (∆HEF) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज HDFC) + \(\frac{1}{2}\)ar (समान्तर चतुर्भुज HABF) = \(\frac{1}{2}\)[ar (समान्तर चतुर्भुज HDFC + ar (समान्तर चतुर्भुज HABF)]
या ar (समान्तर चतुर्भुज EFGH) = \(\frac{1}{2}\)ar(समान्तर चतुर्भुज ABCD) (इति सिद्धम्)

प्रश्न 3.
P और Q क्रमशः समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिन्दु हैं। दर्शाइए कि ar (APB) = ar (BQC) है।
हल:
दिया है-एक समान्तर चतुर्भुज ABCD है, जिसकी भुजाओं DC और AD पर दो बिन्दु P तथा Q स्थित हैं।

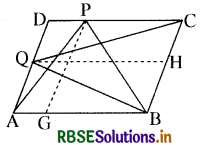
सिद्ध करना हैar (∆APB) = ar (∆BQC)
रचना - अब हमने P बिन्दु से BC के समान्तर PG तथा Q बिन्दु से DC के समान्तर QH रेखा खींची।
उपपत्ति - चित्रानुसार क्योंकि QC, समान्तर चतुर्भुज QHCD का विकर्ण है ।

अतः ar (∆QHC) = Tar (समान्तर चतुर्भुजQHCD).....(i)
पुनः क्योंकि BQ, समान्तर चतुर्भुज ABHQ का विकर्ण है 
अतः ar (∆BQH) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ABHQ) .....(ii)

समीकरण (i) व (ii) को जोड़ने पर ar (∆QHC) + ar (∆BQH) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज QHCD) + \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ABHQ)
या ar (∆BQC) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ABCD)....(iii)
पुनः क्योंकि AP, समान्तर चतुर्भुज़ AGPD का विकर्ण है अतः

ar (∆APG) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज AGPD) .....(iv)
तथा क्योंकि PB, समान्तर चतुर्भुज PCBG का विकर्ण है
अतः ar (∆PBG) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज PCBG) .....(v)
समीकरण (iv) व (v) को जोड़ने पर ar (∆APG) + ar (∆PBG) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ∆GPD) + \(\frac{1}{2}\)ar (समान्तर चतुर्भुज PCBG)

या ar (∆APB) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ABCD).....(vi)
अब समीकरण (iii) व (vi) के आधार पर यह प्राप्त किया जा सकता है कि
ar (∆BQC) = ar (∆APB)(इति सिद्धम् )

प्रश्न 4.
आकृति में, P समान्तर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिन्दु है। दर्शाइए कि
(i) ar (APB) + ar (PCD) = \(\frac{1}{2}\)ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[संकेत : P से होकर AB से समान्तर एक रेखा खींचिए।]

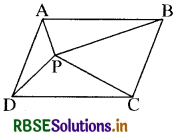
हल:
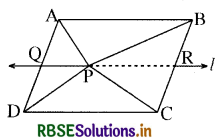
(i) सबसे पहले P बिन्दु से होकर भुजा AB के समान्तर एक रेखा । खींची जो AD को Q बिन्दु पर तथा BC को R बिन्दु पर प्रतिच्छेदित करती है। अब चूँकि ∆APB और समान्तर चतुर्भुज ABRQ एक ही आधार तथा एक ही समान्तर रेखाओं AB और QR के बीच स्थित हैं।
अतः ar (∆APB) = Tar (समान्तर चतुर्भुज ABRO) ....(i)
तथा चूँकि ∆PCD और समान्तर चतुर्भुज DCRQ एक ही आधार DC तथा एक ही समान्तर रेखाओं DC तथा OR के बीच स्थित हैं

अतः ar (∆PCD) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज DCRQ) .....(ii)

समीकरण (i) व (ii) को जोड़ने पर ar (∆APB + ar (∆PCD) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ABRQ) + \(\frac{1}{2}\)ar (समान्तर चतुर्भुज DCRQ) 
या ar (∆APB) + ar (∆PCD) = Tar (समान्तर चतुर्भुज ABCD).....(iii) 

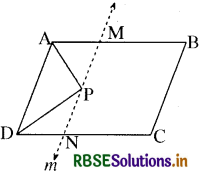
(ii) बिन्दु P से होकर भुजा AD के समान्तर एक रेखा m खींची जो AB को M पर तथा DC को N पर प्रतिच्छेदित करती है। अब चूँकि ∆APD और समान्तर चतुर्भुज ∆MND एक ही आधार AD तथा एक ही समान्तर रेखाओं AD तथा MN के बीच स्थित हैं अतः
ar (∆APD) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज AMND).....(iv)

तथा चूँकि ∆PBC और समान्तर चतुर्भुज MNCB एक ही आधार BC तथा एक ही समान्तर रेखाओं BC और MN के बीच स्थित हैं।
अतः ar (∆PBC) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज MNCB) .....(v)

समीकरण (iv) व (v) को जोड़ने पर। ar (∆APD) + ar (∆PBC) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज AMND) + \(\frac{1}{2}\)ar (समान्तर चतुर्भुज MNCB)
या ar (∆APD) + ar (∆PBC) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ABCD) .....(vi)

अब समीकरण (iii) व (vi) से ar (∆APB) + ar (∆PCD) = ar (∆APD) + ar (∆PBC)
या ar (∆APD) + ar (∆PBC) = ar (∆APB) + ar (∆PCD) (इति सिद्धम्)

प्रश्न 5.
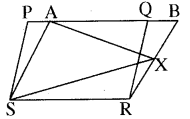
आकृति में, PQRS और ABRS समान्तर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिन्दु है। दर्शाइए कि ।
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = \(\frac{1}{2}\)ar (PQRS)

हल:
(i) प्रश्नानुसार समान्तर चतुर्भुज PORS और समान्तर चतुर्भुज ABRS एक ही आधार SR तथा एक ही समान्तर रेखाओं SR और PB के बीच स्थित हैं
अतः ar (समान्तर चतुभुज PQRS) = ar (समान्तर चतुर्भुज ABRS) .....(i)
क्योंकि हम जानते हैं कि एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित समान्तर चतुर्भुज क्षेत्रफलं में आपस में समान होते हैं।

(ii) प्रश्नानुसार ∆AXS और समान्तर चतुर्भुज ABRS एक ही आधार तथा एक ही समान्तर रेखाओं AS और BR के बीच स्थित हैं।
अतः ar (∆AXS) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज ABRS) ......(ii)
समीकरण (i) व (ii) से ar (∆AXS) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज PQRS) (इति सिद्धम् )

प्रश्न 6.
एक किसान के पास समान्तर चतर्भज PORS के रूप का एक खेत था। उसने RS पर स्थित कोई बिन्दु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है ? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करे? ।
हल:
प्रश्नानुसार PQRS खेत जो कि समान्तर चतुर्भुज के आकार का है, एक किसान के पास था। SR भुजा पर एक A बिन्दु लिया तथा A को बिन्दु P तथा Q से मिला दिया। A बिन्दु को मिलाने पर यह खेत तीन

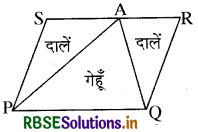
भागों क्रमश: ∆PAS, ∆APQ तथा ∆AQR में विभाजित हो गया। ये तीनों भाग त्रिभुजाकार हैं। अब हम जानते हैं कि ∆APQ और समान्तर चतुर्भुज PQRS एक ही आधार तथा एक ही समान्तर रेखाओं PQ और SR के बीच स्थित हैं। अतः
ar (∆APQ) = \(\frac{1}{2}\)ar (समान्तर चतुर्भुज PQRS)
अर्थात् त्रिभुजाकार भाग APQ, समान्तर चतुर्भुज PQRS के रूप के खेत का आधा भाग है। अतः वह किसान यदि त्रिभुजाकार खेत APQ में गेहूँ बोता है तो दूसरे दो त्रिभुजाकार खेतों क्रमश: PAS तथा AQR में उसे

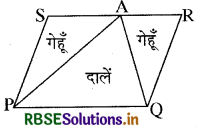
दालें बोनी पड़ेंगी। या यदि वह त्रिभुजाकार खेत APQ में दालें बोता है तो दूसरे दो त्रिभुजाकार खेतों क्रमश: PAS तथा AQR में उसे निश्चित ही गेहूँ बोना पड़ेगा।