RBSE Solutions for Class 9 Maths Chapter 8 चतुर्भुज Ex 8.1

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 8 चतुर्भुज Ex 8.1 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 8 चतुर्भुज Ex 8.1

प्रश्न 1.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल:
माना कि किसी चतुर्भुज ABCD के चारों कोण क्रमशः ∠A, ∠B, ∠C तथा ∠D का अनुपात 3x, 5x, 9x तथा 13x है, जहाँ x एक धनात्मक अचर है।
∴ ∠A + ∠B + ∠C + ∠D = 360°
[क्योंकि चतुर्भुज के चारों कोणों का योग 360° होता है।]
या 3x + 5x + 9x + 13x = 360°
या 30x = 360
या x = \(\frac{360}{30}\) = 12°

अब ∠A = 3x = 3 × 12° = 36°
∠B = 5x = 5 ×12° = 60°
∠C = 9x = 9 × 12° = 108°
∠D = 13x = 13 × 12° = 156°
अतः दिये गये चतुर्भुज के चारों कोण दिए गए अनुपात के आधार पर क्रमशः 36°, 60°, 108° तथा 156° हैं।

प्रश्न 2.
यदि एक समान्तर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है।
हल:
दिया है- प्रश्नानुसार ABCD एक समान्तर चतुर्भुज है जिसमें
विकर्ण AC = विकर्ण BD

सिद्ध करना है - ABCD एक आयत है।
उपपत्ति - विकर्णों के आधार पर ∆ABC और ∆ABD में
AB = AB (उभयनिष्ठ भुजाएँ)
AC = BD (दिया है)
BC = AD (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
∴ ∆ABC = ∆ABD (सर्वांगसमता के नियम SSS के अनुसार)
⇒ ∠DAB = ∠CBA .....(i) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग है)
परन्तु ∠DAB + ∠CBA = 180° .....(ii)
[∵ AD ∥ BC और AB एक तिर्यक रेखा इन्हें काटती है। तिर्यक रेखा के एक ही ओर के अन्त:कोणों का योगफल 180° होता है।] समीकरण (i) व (ii) से
∠DAB = ∠CBA = एक समकोण
अत: ABCD एक आयत है क्योंकि यदि समान्तर चतुर्भुज का एक कोण 90° हो, तो वह आयत होता है। (इति सिद्धम्)

प्रश्न 3.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
हल:
माना कि एक चतुर्भुज ABCD है। इसके विकर्ण AC तथा BD परस्पर एक-दूसरे को बिन्दु ) पर समद्विभाजित करते हैं।
∴ OA = OC, OB = OD
और ∠AOB = ∠BOC = ∠COD
= ∠AOD = 90°
अब हमें यह सिद्ध करना है कि ABCD एक समचतुर्भुज है।

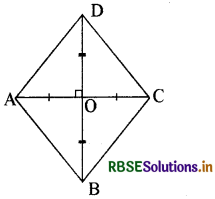
(i) ∆AOD और ∆BOC में
OA = OC (दिया है)
∠AOD = ∠BOC = 90° (दिया है)
तथा OD = OB (दिया है)
अतः ∆AOD = ∆BOC (सर्वांगसमता के नियम SAS के अनुसार)
अतः AD = CB .....(i) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)

(ii) पुन: ∆AOB और ∆COD से
OA = OC (दिया है)
∠AOB = ∠COD = 90° (दिया है)
तथा OB = OD (दिया है)
अत: ∆AOB ≅ ∆COD
(सर्वांगसमता के नियम SAS के अनुसार)
अतः AB = CD (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)

(iii) पुन: ∆AOB और ∆BOC से
AO = OC (दिया है)
∠AOB = ∠BOC = 90° (दिया है) .....(ii)
तथा OB = OB (उभयनिष्ठ भुजा)
अतः ∆AOB ≅ ∆BOC (सर्वांगसमता के नियम SAS के अनुसार)
∴ AB = BC .....(iii) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)

समीकरण (i), (ii) व (iii) से AD = BC = CD = AB इस प्रकार हमने सिद्ध किया कि चतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं तथा इसकी सभी चारों भुजाएँ समान हैं। अतः दिया गया चतुर्भुज उन सभी प्रतिबन्धों को सन्तुष्ट करता है जो एक समचतुर्भुज के लिए आवश्यक हैं। अतः दिया गया चतुर्भुज एक समचतुर्भुज है।

प्रश्न 4.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
हल:
दिया है-एक वर्ग ABCD है जिसमें इसके विकर्ण क्रमश: AC तथा BD हैं।

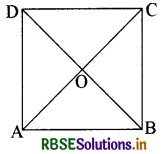
सिद्ध करना है- (i) AC = BD तथा
(ii) AC ⊥ BD

उपपत्ति - (i) विकर्णों के कारण वर्ग में बने ∆ABC और ∆BAD में
AB = AB (उभयनिष्ठ भुजा)
∠ABC = ∠BAD (प्रत्येक 90°) 
तथा BC = AD (वर्ग की भुजाएँ)
अतः ∆ABC ≅ ∆BAD (सर्वांगसमता के नियम SAS के अनुसार)
अर्थात् AC = BD (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं) (इति सिद्धम्)

(ii) पुनः ∆AOB और ∆AOD में
AO = AO (उभयनिष्ठ भुजाएँ)
AB = AD (वर्ग की भुजाएँ)
OB = OD (क्योंकि वर्ग के विकर्ण परस्पर समद्विभाजित करते हैं) 
अतः ∆AOB ≅ ∆AOD
(सर्वांगसमता के नियम SSS के अनुसार)

∠AOB = ∠AOD (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)
लेकिन ∠AOB + ∠AOD = 180° (रैखिक युग्म अभिगृहीत से)
∠AOB = ∠AOD = 90°
अर्थात् AO ⊥ BD
या AC ⊥ BD (इति सिद्धम्)

प्रश्न 5.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर लंबवत् समद्विभाजित करें, तो वह एक वर्ग होता है।
हल:
माना कि एक चतुर्भुज ABCD है जिसके बराबर विकर्ण क्रमश: AC और BD हैं जो एक-दूसरे को O बिन्दु पर समद्विभाजित करते हैं।
अब AC = BD
OA = OC  .....(i)

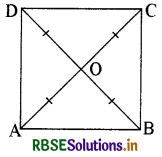
तथा OB = OD .....(ii)
AC = BD
समीकरण (i) व (ii) से
OA + OC = OB + OD
या OC + OC = OB + OB
या 2 OC = 2 OB
या OC = OB .....(iii)

इस प्रकार समीकरण (i), (ii) व (iii) से
OA = OB = OC = OD .....(iv) 

अब ∆AOB और ∆COD से
∠AOB = ∠COD (शीर्षाभिमुख कोण)
OA = OD [(iv) के अनुसार]
तथा OB = OC [(iv) के अनुसार]

अतः ∆AOB ≅ ∆COD
(सर्वांगसमता के नियम SAS के अनुसार)

AB = DC .....(v)
(क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।) इसी प्रकार हम सिद्ध कर सकते हैं कि
∆BOC ≅ ∆AOD

BC = AD .....(vi)
समीकरण (v) व (vi) के आधार पर यह सिद्ध | होता है कि चतुर्भुज ABCD की सम्मुख भुजाएँ बराबर हैं।
अत: ABCD एक समान्तर चतुर्भुज है।
अब ∆ABC और ∆BAD में
AB = AB (उभयनिष्ठ भुजाएँ)

BC = AD [समीकरण (iv) के अनुसार]

तथा AC = BD
अत: ∆ABC ≅ ∆BAD
(सर्वांगसमता के नियम SSS के अनुसार)

∠ABC = ∠BAD .....(vii) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।) परन्तु ZABC + ZBAD = 180° .....(viii)
(∵ ABCD एक समान्तर चतुर्भुज ऊपर प्रमाणित किया है।)

अत: AD ∥ BC तथा AC एक तिर्यक रेखा इनको प्रतिच्छेदित करती है।
अत: ∠ABC + ∠ABC = 180°
[समीकरण (vii) व (viii) के अनुसार]

या 2 ∠ABC = 180°
या ∠ABC = 90°
∴ ∠ABC = ∠BAD = 90° .....(ix)

अर्थात् समान्तर चतुर्भुज के सम्मुख कोण बराबर हैं।
परन्तु ∠ABC = 90° और ∠BAD = 90°
∴ ∠ABC = ∠ADC = 90° .....(x)

तथा ∠BAD = ∠BCD = 90° .....(xi)

इस प्रकार यह कहा जा सकता है कि ∠ABC = ∠ADC = ∠BAD
= ∠BCD = 90° .....(xii)

अब पुनः ∆AOB और ∆BOC में ∠AOB = ∠BOC = 90° (दिया है)
OA = OC (दिया है)

तथा OB = OB (उभयनिष्ठ भुजा)

अर्थात् ∆AOB = ∆COB (सर्वांगसमता के नियम SAS के अनुसार)
अतः AB = BC .....(xiii)

अब समीकरण (v), (vi) तथा (xiii) के अनुसार
AB = BC = CD = AD ....(xiv)

समीकरण (xiii) व (xiv) के आधार पर यह कहा जा सकता है कि हमें ऐसा चतुर्भुज प्राप्त है जिसके बराबर विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं
तथा बराबर भुजाएँ परस्पर 90° का कोण बनाती हैं। अतः दिया गया चतुर्भुज वर्ग के समस्त प्रतिबन्धों को सन्तुष्ट करता है।

प्रश्न 6.
समान्तर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है। ( देखिए आकृति)। दर्शाइए कि

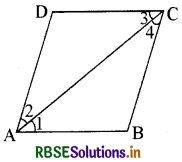
(i) यह ∠C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
हल:
(i) दिया है-एक समान्तर चतुर्भुज ABCD है जिसमें विकर्ण AC, ∠A को समद्विभाजित करता है।
सिद्ध करना है-दिया गया विकर्ण AC, ∠C को भी समद्विभाजित करता है।

उपपत्ति - चित्रानुसार AB ∥ DC तथा AC एक तिर्यक रेखा इन्हें प्रतिच्छेदित करती है।
∴ ∠1 = ∠3 (एकान्तर कोण) .....(i)
∠2 = ∠4 (एकान्तर कोण) .....(ii)

परन्तु ∠1 = ∠2 .....(iii) [क्योंकि AC, CA को समद्विभाजित करती है।]
अतः 73 = 24 अत: AC, ∠C को भी समद्विभाजित करती है।

(ii) सिद्ध करना है-ABCD एक समचतुर्भुज है
भाग (i) से-समीकरण (i), (ii) और (iii) से ∠1 = ∠2 = ∠3 = ∠4

अब ∆ABC में, ∠1 = ∠4 .....(iv) → AB = BC
[त्रिभुज में समान कोणों के सामने की भुजायें समान होती हैं।]

इसी प्रकार ∆ADC में, AD = DC .....(iv) और ABCD एक समान्तर चतुर्भुज है।
∴ AB= CD 
AD = BC .....(vi)

समीकरण (iv), (v) व (vi) से
AB = BC = CD = DA अत: ABCD एक समचतुर्भुज है। (इतिसिद्धम्)

प्रश्न 7.
ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B और D दोनों को समद्विभाजित करता है।
हल:
प्रश्नानुसार ABCD एक समचतुर्भुज है। अतः AB = BC = CD = AD

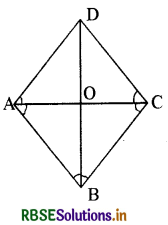
माना कि विकर्ण BD का समद्विभाजक बिन्दु 0 है
अत: OB = OD होगा।
अब ∆AOB तथा ∆AOD से
OA = OA (उभयनिष्ठ भुजाएँ)
AB = AD (समचतुर्भुज की भुजाएँ)

तथा OB = OD
क्योंकि समचतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं।
अत: ∆AOB ≅ ∆AOD
(सर्वांगसमता के SSS नियम के अनुसार)

∴ ∠OAD = ∠OAB (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।)
अर्थात् OA, ∠A को समद्विभाजित करता है। .....(i)

इसी प्रकार ∆BOC ≅ ∆DOC
तथा ∠OCB = ∠OCD = OC, ∠C को समद्विभाजित करता है। .....(ii)
अतः समीकरण (i) व (ii) के आधार पर यह कहा जा सकता है कि विकर्ण AC, ∠A और ∠C को समद्विभाजित करता है।

अब पुनः ∆AOB और ∆BOC में
OB = OB (उभयनिष्ठ भुजाएँ)
AB = BC (समचतुर्भुज की भुजाएँ)

तथा OA = OC
क्योंकि समचतुर्भुज के विकर्ण परस्पर समद्विभाजित करते हैं अतः
∆AOB ≅ ∆COB
(सर्वांगसमता के नियम SSS के अनुसार)

∠OBA = ∠OBC (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।)
अतः OB, ∠B को समद्विभाजित करता है। .....(iii)
इसी प्रकार ∆AOD ≅ ∆COD

तथा ∠ODA = ∠ODC = OD, ∠D को समद्विभाजित करता है। .....(iv)
समीकरण (iii) व (iv) के आधार पर यह कहा जा सकता है कि विकर्ण BD दोनों कोणों B तथा D को समद्विभाजित करता है।

प्रश्न 8.
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है। दर्शाइए कि
(i) ABCD एक वर्ग है
(ii) विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
हल:
प्रश्नानुसार एक आयत ABCD है जिसमें
AB = DC .....(i)
तथा BC = AD

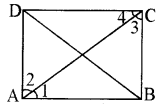
साथ ही प्रत्येक कोण अर्थात ∠A = ∠B = ∠C = ∠D = 90°
(i) बने त्रिभुज ABC और ∆ADC में
∠1 = ∠2 तथा ∠3 = ∠4
क्योंकि विकर्ण AC दोनों कोणों को समद्विभाजित करता है।

तथा AC = AC (उभयनिष्ठ भुजाएँ)
∴ ∆ABC ≅ ∆ADC
(सर्वांगसमता के नियम ASA के अनुसार)

अतः AB = AD .....(ii) समीकरण (i) तथा (ii) से
AB = BC = AD = DC अर्थात् आयत की सभी भुजाएँ समान हैं।
अतः यह एक वर्ग है।

(ii) संलग्न चित्रानुसार

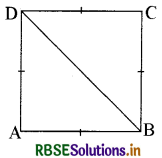
∆ABD तथा ∆BDC में
AB = BC [क्योंकि आयत ABCD एक वर्ग है।]
AD = DC [क्योंकि आयत ABCD एक वर्ग है।]

तथा BD = BD (उभयनिष्ठ भुजाएँ)
अतः ∆ABD ≅ ∆BDC
(सर्वांगसमता के नियम SSS के अनुसार)

∴ ∠ABD = ∠CBD .....(iii) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।)
और ∠ADB = ∠CDB .....(iv) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।)
अतः समीकरण (iii) व (iv) के आधार पर यह कहा जा सकता है कि विकर्ण BD दोनों कोणों B तथा D को समद्विभाजित करता है।

प्रश्न 9.
समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ है ( देखिए आकृति)।

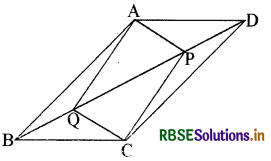
दर्शाइए कि
(i) ∆APD ≅ ∆CQB
(ii) AP = CQ
(iii) ∆AQB ≅ ∆CPD
(iv) AQ = CP
(v) ∆PCQ एक समान्तर चतुर्भुज है।
हल:
(i) प्रश्न में दिए चित्र के ∆APD तथा ∆CQB से
DP = BQ (दिया है)

∠ADP = ∠QBC क्योंकि समान्तर चतुर्भुज ABCD में AD ∥ BC तथा BD एक तिर्यक रेखा उन्हें काटती है।
∴ ∠ADB = ∠DBC (एकान्तर कोण)
∴ ∠ADP = ∠QBC
AD = CB क्योंकि समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।
∴ ∆APD ≅ ∆CQB
(सर्वांगसमता के नियम SAS के अनुसार)

(ii) ∴ AP = CQ (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)

(iii) अब पुनः ∆AQB तथा ∆CPD से BQ = DP (दिया है)
∠ABQ = ∠PDC क्योंकि समान्तर चतुर्भुज ABCD में AB ∥ CD तथा BD एक तिर्यक रेखा इनको काटती है।
∴ ∠ABD = ∠BDC (एकान्तर कोण)
∴ ∠ABQ = ∠PDC
AB = CD क्योंकि समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।

∴ ∆AQB = ∆CPD (सर्वांगसमता के नियम SAS के अनुसार)

(iv) AQ = CP (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं ।)

(v) अब चतुर्भुज ∆PCQ से
AP = CQ (भाग ii से)
तथा AQ = CP (भाग iv से)
अर्थात् चतुर्भुज ∆PCQ की सम्मुख भुजाएँ बराबर हैं। हम जानते हैं कि एक समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।
अतः ∆PCQ एक समान्तर चतुर्भुज है।

प्रश्न 10.
ABCD एक समान्तर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं ( देखिए आकृति)। दर्शाइए कि 

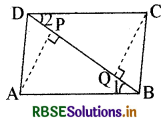
(i) ∆APB ≅ ∆CQD
(ii) AP = CQ.
हल:
प्रश्नानुसार ABCD एक समान्तर चतुर्भुज है जिसमें AB ∥ DC तथा BD एक तिर्यक रेखा है।
∴ ∠1 = ∠2(एकान्तर कोण) .....(i)
(i) अब आकृति में बनने वाले ∆APB और ∆CQD में
∠APB = ∠CQD = 90° (दिया है)
∠1 = ∠2 [समीकरण (i) के अनुसार]
तथा AB = CD [क्योंकि समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं।]
∴ ∆APB ≅ ∆CQD
(सर्वांगसमता के नियम AAS के अनुसार)

(ii) ∴ AP = CQ (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)

प्रश्न 11.
∆ABC और ∆DEF में, AB = DE, AB ∥ DE, BC = EF और BC ∥ EF है। शीर्षों A, B और C को क्रमशः शीर्षों D, E और F से जोड़ा जाता है ( देखिए आकृति) दर्शाइए कि

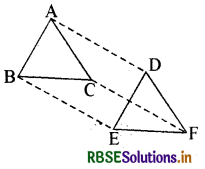
(i) चतुर्भुज ABED एक समान्तर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
(iii) AD ∥ CF और AD = CF है।
(iv) चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
(v) AC = DF है।
(vi) ∆ABC ≅ ∆DEF है।
हल:
प्रश्नानुसार एवं चित्रानुसार दो त्रिभुज ABC और DEF हैं जिसमें AB = DE और AB ∥ DE, साथ ही त्रिभुजों में BC = EF और BC ∥ EF है।

(i) चतुर्भुज ABED में सम्मुख भुजाओं AB और DE का एक युग्म इस प्रकार है कि AB = DE और AB ∥ DE है। अत: ABED एक समान्तर चतुर्भुज है।
∴ AD = BE और AD ∥ BE
क्योंकि समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।  .....(1)

(ii) पुनः चतुर्भुज BEFC में
BE = CF और BE ∥ CF
∴ BEFC एक समान्तर चतुर्भुज है।
CE = BE और CF ∥ BE .....(2)

(iii) समीकरण (1) व (2) से
AD = CF और AD ∥ CF

(iv) ∴ ACFD एक समान्तर चतुर्भुज है क्योंकि यदि चतुर्भुज की सम्मुख भुजाओं का एक युग्म समान और समान्तर हो, तो यह समान्तर चतुर्भुज होता है।

(v) अतः AC = DF क्योंकि ये समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं।

(vi) अब ∆ABC और ∆DEF में AB = DE (दिया है)
BC = EF (दिया है)

तथा AC = DF (भाग v के अनुसार)
∴ ∆ABC = ∆DEF
(सर्वांगसमता के नियम SSS के अनुसार)

प्रश्न 12.
ABCD एक समलम्ब है, जिसमें AB ∥ DC और AD = BC है ( देखिए आकृति)। दर्शाइए कि

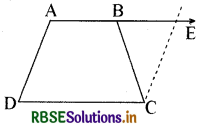
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) विकर्ण AC = विकर्ण BD है।
[संकेत-AB को बढ़ाइए और C से होकर DA के समान्तर एक रेखा खींचिए जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।]
हल:
(i) प्रश्नानुसार दी गई आकृति में AB रेखा को आगे बढ़ाया तथा रेखा CE ∥ AD खींच दी। अब क्योंकि AD ∥ CE और तिर्यक रेखा AE उनको क्रमशः A और E बिन्दुओं पर काटती है।
∴ ∠A + ∠E = 180°
∠A = 180° - ∠E .....(1)
क्योंकि AB ∥ CD तथा AD ∥ CE है

अतः ∆ECD एक समान्तर चतुर्भुज है। अर्थात्
AD = CE
BC = CE [क्योंकि AD = BC (दिया है)]

अत: ∆BCE में
BC = CE
⇒ ∠CBE = ∠CEB
क्योंकि बराबर भुजाओं के सम्मुख कोण भी बराबर होते हैं।
∴180° - ∠B = ∠E
[∵ ∠CBE + ∠ABC = 180° (रैखिक युग्म अभिगृहीत से)]
∴ ∠CBE = 180° - ∠ABC
⇒ 180° - ∠E = ∠B .....(2)

समीकरण (1) व (2) से ∠A = ∠B
(ii) ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC
∴ ∠A+ ∠D = 180°
तथा ∠B + ∠C = 180° ......(4)
क्योंकि दो समान्तर रेखाओं के लिए तिर्यक रेखा के एक ही ओर के दो अन्त:कोणों का योगफल 180° होता है।

समीकरण (3) व (4) से 
∠A + ∠D = ∠B + ∠C
परन्तु ∠A = ∠B (सिद्ध कर चुके हैं)

∠A + ∠D = ∠A + ∠C
⇒ ∠D = ∠C
या ∠C = ∠D (इति सिद्धम् )

(iii) दिए गए ∆ABC और ∆BAD में ।
AB = AB (उभयनिष्ठ भुजाएँ)
∠A = ∠B (सिद्ध कर चुके हैं)
तथा BC = AD (दिया है)

∴ ∆ABC ≅ ∆BAD
(सर्वांगसमता के नियम SAS के अनुसार)

(iv) अत: AC = BD (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)
अतः यह कहा जा सकता है कि समलम्ब चतुर्भुज ABCD में विकर्ण AC = विकर्णBD.