RBSE Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 7 त्रिभुज Ex 7.5 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 7 त्रिभुज Ex 7.5

प्रश्न 1.
ABC एक त्रिभुज है। इसके अभ्यंतर में एक ऐसा बिन्दु ज्ञात कीजिए जो ∆ABC के तीनों शीर्षों से समदूरस्थ है।
हल:
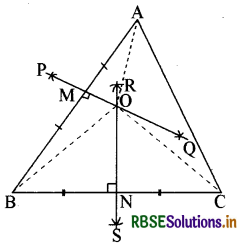
माना कि ABC एक त्रिभुज है। इसकी भुजाओं AB और BC के लंब समद्विभाजक क्रमशः PQ और RS खींचिए। माना कि PQ, AB को M पर समद्विभाजित करता है और RS, BC को बिन्दु N पर समद्विभाजित करता है।
मान लीजिए PQ और RS बिन्दु 0 पर प्रतिच्छेद करते हैं। OA, OB और OC को मिलाइए। अब, ∆AOM और BOM में
AM = MB . (रचना से)
∠AMO = ∠BMO
[प्रत्येक 90° (रचना से)]

OM = OM (उभयनिष्ठ भुजाएँ)
∴ ∆AOM = ∆BOM
(सर्वांगसमता के नियम SAS के अनुसार)

इसलिए, OA = OB (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग).....(i)
इसी तरह, ∆BON = ∆CON
⇒ OB = OC (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग).....(ii)

(i) और (ii) के आधार पर
OA = OB = OC
अतः ∆ABC की किन्हीं दो भुजाओं के लंब समद्विभाजकों का प्रतिच्छेद बिन्दु O, इसके तीनों शीर्षों से समदूरस्थ है।

प्रश्न 2.
किसी त्रिभुज के अभ्यंतर में एक ऐसा बिन्दु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समदूरस्थ हो।
हल:
माना कि ABC एक त्रिभुज है। अब ∠B और ∠C के समद्विभाजक खींचिए।
माना कि ये कोण समद्विभाजक परस्पर बिन्दु I पर प्रतिच्छेद करते हैं। अब IK ⊥ BC खींचिए।

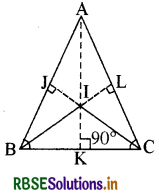
साथ ही, IJ ⊥ AB
और IL ⊥ AC खींचिए।
AI को मिलाइए।

∆BIK और ∆BIJ के अनुसार,
∠IKB = ∠IJB . (प्रत्येक 90°) (रचना से)
∠IBK = ∠IBJ [क्योंकि BI ∠B का समद्विभाजक है] (रचना से)
BI = BI (उभयनिष्ठ भुजाएँ)

∴ ∆BIK = ∆BIJ
(सर्वांगसमता के नियम AAS के अनुसार)
IK = IJ (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग).....(i)

इसी प्रकार,
∆CIK ≅ ∆CIL
इसलिए, IK = IL (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग).....(ii)

(i) और (ii) के आधार पर
IJ = IK = IL;
अंतः ∆ABC के किन्हीं दो कोणों को समद्विभाजकों का प्रतिच्छेद बिन्दु I इसकी भुजाओं से समदूरस्थ है।

प्रश्न 3.
एक बड़े पार्क में लोग तीन बिन्दुओं (स्थानों) पर केन्द्रित हैं ( देखिए आकृति)।

स्थल और बाहर निकलने के रास्ते के निकट है। एक आइसक्रीम का स्टाल कहाँ लगाना चाहिए ताकि वहाँ लोगों की अधिकतम संख्या पहुँच सके ?
हल:
स्टाल A, B और C से समदूरस्थ होना चाहिए। इसके लिए हम बिन्दुओं B और C को मिलाने वाली रेखा का लम्ब समद्विभाजक l और बिन्दुओंA और C को मिलाने वाली रेखा का लंब समद्विभाजक m खींचते हैं।

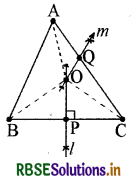
अब माना कि l और m परस्पर बिन्दु O पर

प्रतिच्छेद करते हैं। अब बिन्दु O बिन्दुओं A, B और C से समदूरस्थ हैं।
OA, OB और OC को मिलाइए।

उपपत्ति - ∆BOP और ∆COP में,
OP = OP (उभयनिष्ठ भुजाएँ)

∠OPB = ∠OPC (प्रत्येक = 90°) (रचना से)
BP = PC [क्योंकि P, BC का मध्य-बिन्दु है]

∆BOP ≅ ∆COP [सर्वांगसमता के नियम SAS के अनुसार]
इसलिए, OB = OC (क्योंकि ये
सर्वांगसम त्रिभुजों के संगत भाग) .....(i)
इसी तरह, ∆AOQ ≅ ∆COQ
⇒ OA = OC (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग.).....(ii)

(i) और (ii) के अनुसार
OA = OB = OC हम देखते हैं कि इन बिन्दुओं को मिलाने से प्राप्त तीन भुजाओं में से किन्हीं दो भुजाओं के लम्ब समद्विभाजकों का प्रतिच्छेद बिन्दु 0 ही वह बिन्दु है जहाँ पर आइसक्रीम स्टाल लगाना चाहिए।

प्रश्न 4.
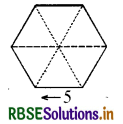
षड्भुजीय और तारे के आकार की रंगोलियों [ देखिए आकृति (i) और (ii)] को 1 cm भुजा वाले समबाहु त्रिभुजों से भरकर पूरा कीजिए। प्रत्येक स्थिति में, त्रिभुजों की संख्या गिनिए। किसमें अधिक त्रिभुज हैं ?

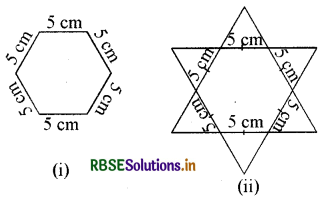
हल:
षड्भुजीय रंगोली में--प्रत्येक 5 cm भुजा वाली समबाहु त्रिभुजों की संख्या 5 cm भुजा वाली समबाहु त्रिभुज का क्षेत्रफल

\(\frac{\sqrt{3}}{4}\) (भुजा)
= (5) = 9525
षड्भुजीय रंगोली का क्षेत्रफल = 6 × एक
समबाहु त्रिभुज का क्षेत्रफल = 6 × \(\frac{\sqrt{3}}{4}\) × 25
= 150 × \(\frac{\sqrt{3}}{4}\)cm² .....(i)

1 cm भुजा वाली समबाहु त्रिभुज का क्षेत्रफल
= \(\frac{\sqrt{3}}{4}\)(1)²
= \(\frac{\sqrt{3}}{4}\)cm .....(ii)
षड्भुजीय रंगोली में 1 cm भुजा वाले समबाहु त्रिभुजों की संख्या
= 150\(\frac{\sqrt{3}}{4} \div \frac{\sqrt{3}}{4}\)
= 150\(\frac{\sqrt{3}}{4} \times \frac{4}{\sqrt{3}}\)
= 150 .....(iii)

अब तारे के आकार की रंगोली में
प्रत्येक 5 cm भुजा वाली समबाहु त्रिभुजों की संख्या = 12

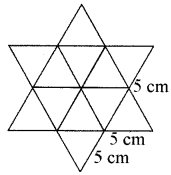
इसलिए तारे के आकार वाली रंगोली का कुल क्षेत्रफल = 12 × 5 cm भुजा वाली एक समबाहु त्रिभुज का क्षेत्रफल .
=125(\(\frac{\sqrt{3}}{4}\) × (5)²)
= 12 × \(\frac{\sqrt{3}}{4}\) × 25
= 300\(\frac{\sqrt{3}}{4}\) cm² ....iv)

तारे के आकार वाली रंगोली में 1 cm. भुजा वाली त्रिभुजों की संख्या जा रहा है या मा गोपाल
= 3000\(\frac{\sqrt{3}}{4} \div \frac{\sqrt{3}}{4}\)
[समीकरण (iv) में (ii) से भाग देने पर]
= 3000\(\frac{\sqrt{3}}{4} \times \frac{4}{\sqrt{3}}\)
= 300 समीकरण (iii) और (v) से हम देखते हैं कि तारे के आकार वाली रंगोली में 1 cm भुजा वाली समबाहु त्रिभुजों की संख्या अधिक है।