RBSE Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.5

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.5 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 7 Triangles Exercise 7.5

Question 1.
∆BC is a triangle. Locate a point in the interior of ∆ABC which is equidistant from all the vertices of ∆ABQ,
Answer:

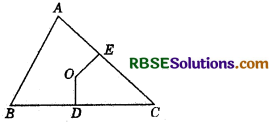
Let OD and OE be the perpendicular bisectors of sides BC and CA of ∆ABC.
∴ O is equidistant from two end points B and C of line-segment BC as O lies on the perpendicular bisector of BC.
Similarly, O is equidistant from C and A.
Thus, the point of intersection O of the perpendicular bisectors of sides BC and CA (or AB) is the required point.

Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Answer:

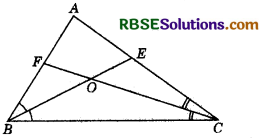
Let BE and CF be the bisectors of ∠ABC and ∠ACB respectively intersecting AC and AB at E and F respectively.
Since, O lies on the bisector BE of ∠ABC, hence, O will be equidistant from BA and BC. Again, O lies on the bisector CF of ∠ACB. Hence, O will be equidistant from CB and CA. Thus, O will be equidistant from AB, BC and CA.

Question 3.
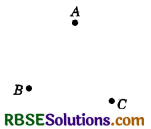
In a huge park, people are concentrated at three points (see figure) :
A : where there are different slides and swings for children,
B : near which a man-made lake is situated,
C : which is near to a large parking and exit.
Where should an icecream parlour be set up so that maximum number of persons can approach it?
(Hint: The parlour should be equidistant from A, B, and C)

Answer:

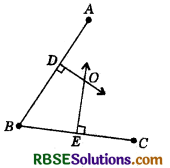
The parlour should be equidistant from A, B and C, for which the point of intersection of perpendicular bisectors of AB, BC and CA should be located.
Thus, O is the required point which is equidistant from A, B and C.

Question 4.
Complete the hexagonal and star shaped Rangolies [see figure (i) and (ii)] by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?

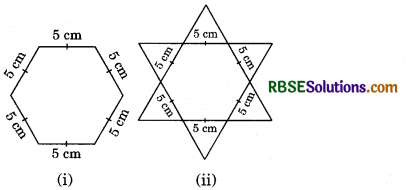
Answer:

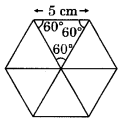
Let us first divide the given hexagon into six
equilateral triangles of side 5 cm as shown alongside.
Now take one such triangle and make as many equilateral
triangles of 1 side 1 cm as we can as shown in the figure:
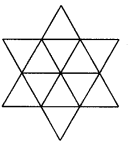
Number of equilateral triangles of side 1 cm
= 9 + 7 + 5 + 3 + 1 = 25
∴ Total number of triangles in the hexagon = 6 × 25 = 150.
Similarly, we can find the number of triangles in the figure (ii) = 12 × 25 = 300.