RBSE Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.4

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.4 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 7 Triangles Exercise 7.4

Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.

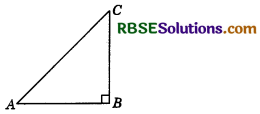
Answer:
Let ABC be a right-angled triangle, in which ∠ABC = 90°.
But ∠ABC + ∠BCA + ∠CAB = 180°
⇒ 90° + ∠BCA + ∠CAB = 180°
⇒ ∠BCA + ∠CAB = 90°
⇒ ∠BCA and ∠CAB are acute angles.
⇒ ∠BCA < 90° and ∠CAB < 90°
⇒ ∠BCA < ∠ABC and ∠CAB < ∠ABC ⇒ AC > AB and AC > BC (∵ Side opp. to greater angle is larger.)
⇒ In a right triangle, the hypotenuse is the longest side.

Question 2.
In the figure, sides AB and AC of ∆ ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

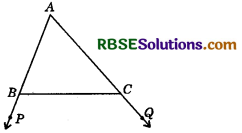
Solution :
Since ∠PBC < ∠QCB, therefore - ∠PBC > - ∠QCB
or 180° - ∠PBC > 180° - ∠QCB
or ∠ABC > ∠ACB
So, AC > AB (∵ Side opp. to greater angle is larger.)
Hence proved.

Question 3.
In the figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

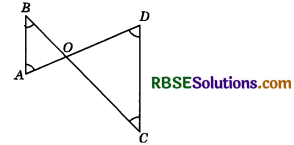
Answer:
Since ∠B < ∠A and ∠C < ∠D
∴ AO < BO
and OD < OC
(∵ Side opp. to greater angle is larger.)
Adding these results, we have :
AO + OD < BO+ OC
So, AD < BC. Hence proved. Question 4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A > ∠C and ∠B > ∠D.

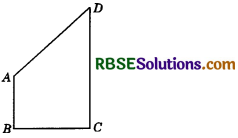
Answer:
ABCD is a quadrilateral such that AB is its smallest side and CD is its longest side.
Join AC and BD.

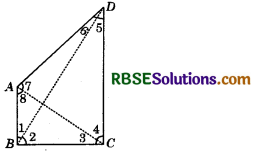
Since AB is the smallest side of quadrilateral ABCD, therefore in ∆ABC, we have :
BC > AB
So, ∠8 > ∠3 ......... (1)
(∵ Angle opp. to longer side is greater.)
Since CD is the longest side of quadrilateral ABCD, therefore in ∆ACD, we have:
CD > AD
So, ∠7 > ∠4 ......... (2) (∵ Angle opp. to longer side is greater.)
Adding (1) and (2), we get:
∠8 + ∠7 > ∠3 +∠4
∴ ∠A > ∠C
Again, in ∆ABD, we have:
AD > AB
So, ∠1 > ∠6
In ∆BCD, we have :
CD > BC
So,∠2 > ∠5
Adding (3) and (4), we get:
∠1 + ∠2 > ∠5 + ∠6 ⇒ ∠B > ∠D
Thus, ∠A > ∠C and ∠B > ∠D.

Question 5.
In the figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

Answer:
In APQR, we have :
PR > PQ (Given)
So, ∠PQR > ∠PRQ
(∵ Angle opp. to longer side is greater.)
∴ ∠PQR + ∠1 > ∠PRQ + ∠1
⇒ ∠PQR + ∠1 > ∠PRQ + ∠2 (∵ PS is the bisector of ∠P ∴ ∠1 = ∠2)
Now, in ∆s PQS and PSR, we have:
∠PQR + ∠1 + ∠PSQ = 180°
and ∠PRQ + ∠2 + ∠PSR = 180°
so, ∠PQR + ∠1 = 180° - ∠PSQ
and ∠PRQ + ∠2 = 180° - ∠PSR
∴ 180° - ∠PSQ > 180° - ∠PSR [From (1)]
or - ∠PSQ > - ∠PSR
or ∠PSQ < ∠PSR, i.e., ∠PSR > ∠PSQ.
Hence Proved.

Question 6.
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Answer:

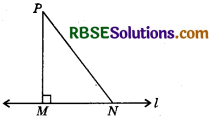
Let P be any point not on the straight line l. PM ⊥ l and N is any point on l other than M.
In ∆PMN, we have: ∠M = 90°
∴ ∠N < 90°
(∵ ∠M = 90° ⇒ ∠MPN + ∠PNM = 90°
⇒ ∠P + ∠N = 90° ⇒ ∠N < 90°)
or ∠N < ∠M
So, PM < PN
(∵ Side opp. to greater angle is longer.)
Hence, PM is the shortest of all line segments from P to AB.
Hence proved.