RBSE Solutions for Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.2

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.2 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.2

प्रश्न 1.
आप यूक्लिड की पाँचवीं अभिधारणा को किस प्रकार लिखेंगे ताकि वह सरलता से समझी जा सके?
हल:
गणित के इतिहास में यूक्लिड की पाँचवीं अभिधारणा का अत्यधिक महत्त्व है। इस अभिधारणा के परिणामस्वरूप यदि दो रेखाओं पर गिरने वाली रेखा के एक ही कोने के दोनों अंत:कोणों का योग 180° हो, तो दोनों रेखाएँ कभी भी प्रतिच्छेद नहीं कर सकतीं। इस अभिधारणा के अनेक समतुल्य रूपान्तरण (equivalent versions) हैं। इनमें से एक प्लेफेयर का अभिगृहीत (Playfair's Axiom) है (जिसे स्काटलैंड के एक गणितज्ञ जॉन प्लेफेयर ने 1729 में दिया था)। यह इस प्रकार है-

प्रत्येक रेखा l और उस पर न स्थित प्रत्येक बिन्दु P के लिए, एक अद्वितीय रेखा m ऐसी होती है जो P से होकर जाती है और l के समान्तर है।

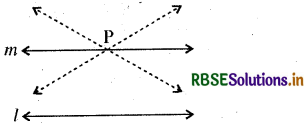
आकृति में आप देख सकते हैं कि P से होकर जाने वाली सभी रेखाओं में से केवल m ही रेखा l के समान्तर है।
इस परिणाम को निम्नलिखित रूप में भी व्यक्त किया जा सकता है
दो भिन्न प्रतिच्छेदी रेखाएँ एक ही रेखा के समान्तर नहीं हो सकतीं।

प्रश्न 2.
क्या यूक्लिड की पाँचवीं अभिधारणा से समान्तर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है ? स्पष्ट कीजिए।
हल:
हाँ। यूक्लिड की पाँचवीं अभिधारणा से समान्तर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है क्योंकि यदि कोई सरल रेखा। दो सरल रेखाओं m तथा n पर इस प्रकार पड़ती हो कि । के एक ही ओर के __ अन्त:कोणों का योग दो समकोण हो तो यूक्लिड की पाँचवीं अभिधारणा के अनुसार यह रेखा । के इस ओर नहीं मिलेगी।

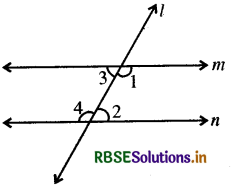
यह भी हम जानते हैं कि रेखा । के दूसरी ओर के अन्त: कोणों का योग भी दो समकोण होगा। अत: दूसरी ओर भी यह नहीं मिलेगी। अत: रेखाएँ m तथा n कभी भी नहीं मिलेंगी तथा इसीलिए ये रेखाएँ m तथा n समान्तर होंगी।
यदि m || n है तो
∠1 + ∠2 = 2 समकोण (अन्त:कोणों का योग)
तथा ∠3 + ∠4 = 2 समकोण (अन्तःकोणों का योग)