RBSE Solutions for Class 9 Maths Chapter 15 प्रायिकता Ex 15.1

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 15 प्रायिकता Ex 15.1 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 15 प्रायिकता Ex 15.1

प्रश्न 1.
एक क्रिकेट मैच में, एक महिला बल्लेबाज खेली गई 30 गेंदों में 6 बार चौका मारती है। चौका न मारे जाने की प्रायिकता ज्ञात कीजिए।
हल:
महिला बल्लेबाज द्वारा खेली गई गेंदें = 30
उन गेंदों की संख्या जिन पर चौका मारा = 6
ऐसी गेंदों की संख्या जिन पर चौका नहीं लगा = 30 - 6 = 24
P(प्रायिकता) =

= \(\frac{24}{30}=\frac{4}{5}\) 
अतः महिला बल्लेबाज द्वारा चौका न मारे जाने की प्रायिकता 4 है।

प्रश्न 2.
2 बच्चों वाले 1500 परिवारों का यदृच्छया चयन किया गया है और निम्नलिखित आँकड़े लिख लिए गए हैं

यदृच्छया चुने गए उस परिवार की प्रायिकता ज्ञात कीजिए, जिसमें-
(i) दो लड़कियाँ हों
(ii) एक लड़की हो
(iii) कोई लड़की न हो
साथ ही, यह भी जाँच कीजिए कि इन प्रायिकताओं का योगफल 1 है या नहीं।
हल:
(i) परिवारों की कुल संख्या = 1500
2 लड़कियों वाले परिवारों की संख्या = 475
अतः उन परिवारों की प्रायिकता जिनके दो लड़कियाँ हों (P)

(ii) एक लड़की वाले परिवारों की संख्या = 814
∴ प्रायिकता (P)

(iii) बिना लड़की वाले परिवारों की कुल संख्या = 211
∴ प्रायिकता (P)

अर्थात् सभी प्रायिकताओं का योगफल 1 है। 

प्रश्न 3.
अध्याय 14 के अनुच्छेद 14.4 का उदाहरण 5 लीजिए। कक्षा के किसी एक विद्यार्थी का जन्म अगस्त में होने की प्रायिकता ज्ञात कीजिए।
हल:
अध्याय 14 के अनुच्छेद 14.4 के उदाहरण 5 के अनुसार कक्षा 9 के विद्यार्थियों की कुल संख्या = 40
तथा अगस्त मास में जन्मे विद्यार्थियों की कुल संख्या = 6
∴ प्रायिकता (P).

प्रश्न 4.
तीन सिक्कों को एक साथ 200 बार उछाला गया है तथा इनमें विभिन्न परिणामों की बारम्बारताएँ ये हैं

यदि तीनों सिक्कों को पुनः एक साथ उछाला जाए, तो दो चित के आने की प्रायिकता ज्ञात कीजिए।
हल:
दो चित आने की बारम्बारता = 72
∴  दो चित आने की प्रायिकता (P)

प्रश्न 5.
एक कम्पनी ने यदृच्छया 2400 परिवार चुनकर एक घर की आय स्तर और वाहनों की संख्या के बीच सम्बन्ध स्थापित करने के लिए उनका सर्वेक्षण किया। एकत्रित किए गए आंकड़े नीचे सारणी में दिए गए हैं-

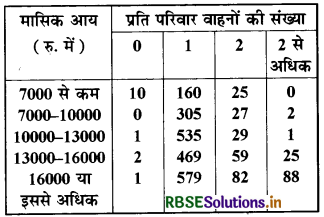
मान लीजिए एक परिवार चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गए परिवार
(i) की आय 10000-13000 रु. प्रति माह है और उसके पास ठीक-ठीक दो वाहन हैं।
(ii) की आय प्रति माह 16000 रु. या इससे अधिक है और उसके पास ठीक 1 वाहन है।
(iii) की आय 7000 रु. प्रति माह से कम है और उसके पास कोई वाहन नहीं है।
(iv) की आय 13000-16000 रु. प्रति माह है और उसके पास 2 से अधिक वाहन हैं।
(v) जिसके पास 1 से अधिक वाहन नहीं है।
हल:
कम्पनी द्वारा यदृच्छया सर्वेक्षित परिवारों की संख्या = 2400
(i) प्रश्नानुसार 10000-13000 रु.
प्रतिमाह आय वाले और ठीक-ठीक दो वाहन रखने वाले परिवारों की संख्या = 29
∴ इनकी प्रायिकता (P₁) = \(\frac{29}{2400}\)

(ii) प्रश्नानुसार ऐसे परिवारों की कुल संख्या जिनकी 'आय प्रतिमाह 16000 रु. या इससे अधिक है तथा उनके पास ठीक एक वाहन है = 579
∴ इनकी प्रायिकता (P₂) = \(\frac{579}{2400}\)

(iii) ऐसे परिवारों की संख्या जिनकी आय 7000 रु. से भी कम है और उनके पास कोई वाहन नहीं है = 10
∴ इनकी प्रायिकता (P) = \(\frac{10}{2400}=\frac{1}{240}\) 

(iv) ऐसे परिवारों की संख्या जिनकी आय 13,000--16,000 रु. प्रति माह है तथा उनके पास 2 से अधिक वाहन हैं = 25
∴ इनकी प्रायिकता (P) = \(\frac{25}{2400}=\frac{1}{96}\) 

(v) ऐसे परिवारों की संख्या जिनके पास 1 से अधिक वाहन नहीं हैं = कोई भी वाहन न रखने वाले परिवारों की संख्या + केवल एक वाहन
रखने वाले परिवारों की संख्या
= (10 + 0 + 1 + 2 + 1) + (160 + 305 + 535 + 469 + 579)
= 14 + 2048
= 2062
∴ इनकी प्रायिकता (P) = \(\frac{2062}{2400}=\frac{1031}{1200}\)

प्रश्न 6.
अध्याय 14 की सारणी 14.7 लीजिए।
(i) गणित की परीक्षा में एक विद्यार्थी द्वारा 20% कम अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(ii) एक विद्यार्थी द्वारा 60 या इससे अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
हल:
अध्याय 14 की सारणी 14.7 के अनुसार विद्यार्थियों की कुल संख्या = 90
(i) प्रश्नानुसार 20% से कम अंक प्राप्त करने वाले विद्यार्थियों की संख्या = 7
∴ इनकी प्रायिकता (P)

(ii) विद्यार्थी द्वारा 60 या इससे अधिक अंक प्राप्त करने वाले विद्यार्थियों की संख्या = (60 - 70) अंक प्राप्त करने वाले विद्यार्थी + 70 और अधिक अंक प्राप्त करने वाले विद्यार्थी
= 15 + 8
= 23
∴ इनकी प्रायिकता (P)

प्रश्न 7.
सांख्यिकी के बारे में विद्यार्थियों का मत जानने के लिए 200 विद्यार्थियों का सर्वेक्षण किया गया। प्राप्त आँकड़ों को नीचे दी गई सारणी में लिख लिया गया है-

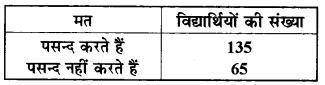
प्रायिकता ज्ञात कीजिए कि यदृच्छया चुना गया विद्यार्थी
(i) सांख्यिकी पसन्द करता है
(ii) सांख्यिकी पसन्द नहीं करता है।
हल:
सांख्यिकी के बारे में विद्यार्थियों का मत जानने हेतु सर्वेक्षित छात्र = 200
(i) प्रश्नानुसार सांख्यिकी को पसन्द करने वाले विद्यार्थियों की संख्या = 135
∴ इनकी प्रायिकता (P)

(ii) पुनः प्रश्नानुसार सांख्यिकी को पसन्द न करने वाले विद्यार्थियों की संख्या = 65
∴ इनकी प्रायिकता (P)

प्रश्न 8.
प्रश्नावली 14.2 का प्रश्न 2 देखिए। इसकी आनुभविक प्रायिकता क्या होगी कि इंजीनियर
(i) अपने कार्यस्थल से 7 km से कम दूरी पर रहती है?
(ii) अपने कार्यस्थल से 7 km या इससे अधिक दूरी पर रहती है?
(iii) अपने कार्यस्थल से \(\frac{1}{2}\)km या इससे कम दूरी पर रहती है?
हल:
प्रश्नावली 14.2 के प्रश्न 2 के अनुसार इंजीनियरों की कुल संख्या = 40
(i) प्रश्नानुसार अपने कार्यस्थल से 7 km दूर रहने वाले इंजीनियरों की संख्या = 9
∴ इनकी प्रायिकता (P)

(ii) प्रश्नानुसार अपने कार्यस्थल से 7 km या इससे अधिक दूरी पर रहने वाले इंजीनियरों की संख्या = 31
∴  इनकी प्रायिकता (P)

(iii) प्रश्नानुसार अपने कार्यस्थल से }km या इससे कम दूरी पर रहने वाले इंजीनियरों की संख्या = 0
∴ इनकी प्रायिकता (P)

प्रश्न 9.
क्रियाकलाप: अपने विद्यालय के गेट के सामने से एक समय-अन्तराल में गुजरने वाले दो पहिया, तीन पहिया और चार पहिया वाहनों की बारम्बारता लिख लीजिए। आप द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता ज्ञात कीजिए।
हल:
माना कि आपने अपने विद्यालय के सामने से गेट के बाहर से गुजरने वाले दो पहिया, तीन पहिया तथा चार पहिया वाहनों को मध्यान्तर या अन्तर्वेला में देखा है जो निम्न सारणी के अनुसार है

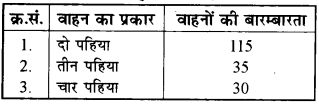
आप द्वारा देखे गए वाहनों में से किसी एक वाहन का दो पहिया वाहन होने की प्रायिकता (P)

प्रश्न 10.
क्रियाकलाप : आप अपनी कक्षा के विद्यार्थियों से एक 3 अंक वाली संख्या लिखने को कहिए। आप कक्षा से एक विद्यार्थी को यदृच्छया चुन लीजिए। इस बात की प्रायिकता क्या होगी कि उसके द्वारा लिखी गई संख्या 3 से भाज्य है ? याद रखिए कि कोई संख्या 3 से भाज्य होती है, यदि उसके अंकों का योग 4 से भाज्य हो।
हल:
तीन अंकों वाली संख्याएँ 100 से प्रारम्भ होकर 999 तक हैं। 100 से 999 तक के बीच कुल सम्भावित संख्याएँ 900 हैं। इन नौ सौ संख्याओं में प्रत्येक तीसरी संख्या 3 से विभाज्य होगी।
इस प्रकार 3 अंकों वाली कुल संख्याएँ = 900
3 से विभाज्य 3 अंकों वाली कुल संख्याएँ
= \(\frac{900}{3}\) = 300
अतः छात्र द्वारा लिखी गई संख्या 3 से विभाज्य होने की प्रायिकता
= \(\frac{300}{900}=\frac{1}{3}\)

प्रश्न 11.
आटे की उन ग्यारह थैलियों में, जिन पर 5 kg अंकित है, वास्तव में आटे के निम्नलिखित भार (kg में) हैं
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00.
यदृच्छया चुनी गई एक थैली में 5 kg से अधिक आटा होने की प्रायिकता क्या होगी?
हल:
आटे की कुल थैलियों की संख्या = 11
5kg से अधिक आटे वाली थैलियों की संख्या = 7
∴ इसकी प्रायिकता (P)

प्रश्न 12.
प्रश्नावली 14.2 के प्रश्न 5 में आपसे 30 दिनों तक एक नगर की प्रति वायु में सल्फर डाइ ऑक्साइड की भाग प्रति मिलियन में सान्द्रता से सम्बन्धित एक बारम्बारता बंटन सारणी बनाने के लिए कहा गया था। इस सारणी की सहायता से इनमें से किसी एक दिन अन्तराल (0.12-0.16) में सल्फर डाई-ऑक्साइड के सान्द्रण होने की प्रायिकता ज्ञात कीजिए।
हल:
प्रश्नावली 14.2 के प्रश्न 5 के अनुसार एक दिन अन्तराल (0.12-0.16) की बारम्बारता = 2
प्रश्नानुसार दिनों की कुल संख्या = 30
∴ सान्द्रण होने की प्रायिकता (P)

प्रश्न 13.
प्रश्नावली 14.2 के प्रश्न 1 में आप से एक कक्षा के 30 विद्यार्थियों के रक्त-समूह से सम्बन्धित बारम्बारता बंटन सारणी बनाने के लिए कहा गया था। इस सारणी की सहायता से इस कक्षा से यदृच्छया चुने गए एक विद्यार्थी का रक्त समूह AB होने की प्रायिकता ज्ञात कीजिए।
हल:
प्रश्नावली 14.2 के प्रश्न 1 के अनुसार विद्यार्थियों की कुल संख्या = 30
तथा रक्त समूह AB के विद्यार्थियों की संख्या = 3
अतः कक्षा से यदृच्छया चुने गए एक विद्यार्थी का AB रक्त समूह होने की प्रायिकता (P).