RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.7

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.7 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.7

प्रश्न 1.
उस लम्ब वृत्तीय शंकु का आयतन ज्ञात कीजिए, जिसकी
(i) त्रिज्या 6 cm और ऊँचाई 7 cm है।
(ii) त्रिज्या 3.5 cm और ऊँचाई 12 cm है।
हल:
(i) प्रश्नानुसार लम्ब वृत्तीय शंकु की त्रिज्या (r) = 6 cm
तथा ऊँचाई (h) = 7 cm
∴ शंकु का आयतन = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 6 × 6 × 7
= 264 cm³.

(ii) लम्ब वृत्तीय शंकु की त्रिज्या (r) = 3.5 cm
तथा ऊँचाई (h) = 12 cm
∴ शंकु का आयतन = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 3.5 × 3.5 × 12
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{35}{10} \times \frac{35}{10}\) × 12
= 154 cm³

प्रश्न 2.
शंकु के आकार के उस बर्तन की लीटरों में धारिता ज्ञात कीजिए जिसकी
(i) त्रिज्या 7 cm और तिर्यक ऊँचाई 25 cm है।
(ii) ऊँचाई 12 cm और तिर्यक ऊँचाई 13 cm है।
हल:
(i) प्रश्नानुसार यहाँ r = 7 cm, 1 = 25 cm
l² = r² + h²
h² = l² - h²
= (25)² – (7)²
= 625 - 49
h² = 576
∴ h = \(\sqrt{576}\) = 24 cm

अब शंकु के आकार वाले बर्तन की धारिता
= \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 7 × 24
= 1232 cm³
∵ हम जानते हैं कि 1000 cm³ = 1 लीटर
= \(\frac{1232}{1000}\) = 1.232 l

(ii) यहाँ h = 12 cm
तथा तिर्यक ऊँचाई (l) = 13 cm
∵ l² = r² + h²
या r² = h² - l²
= (13)² - (12)²
= 169 - 144
r² = 25
r = /25 = 5 cm

∴ शंकु के आकार के बर्तन की धारिता = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 5 × 5 × 12
= \(\frac{2200}{7}\) cm
= \(\frac{2200}{7} \times \frac{1}{1000}\) l
(∵ 1l = 1000 cm³)
= \(\frac{11}{35}\)l

प्रश्न 3.
एक शंकु की ऊँचाई 15 cm है। यदि इसका आयतन 1570 cm है, तो इसके आधार की त्रिज्या ज्ञात कीजिए। (π = 3.14 प्रयोग कीजिए।)
हल:
प्रश्नानुसार शंकु की ऊँचाई (h) = 15 cm
शंकु का आयतन = 1570 cm³
माना कि शंकु की त्रिज्या r है।
∴ \(\frac{1}{3}\)πr²h = 1570
या \(\frac{1}{3}\) × 3.14 × r² × 15 = 1570
या 15.707r² = 1570
या r² = \(\frac{1570}{1570}\) × 100
∴ r = \(\sqrt{100}\)
= 10 cm

प्रश्न 4.
यदि 9 cm ऊँचाई वाले एक लम्ब वृत्तीय शंकु का आयतन 48 m cm है, तो इसके आधार का व्यास ज्ञात कीजिए।
हल:
प्रश्नानुसार शंकु का आयतन
= 48 π cm ......(i)

शंक की ऊँचाई (h) = 9 cm
माना कि शंकु की त्रिज्या r है।
∵ शंकु का आयतन = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\)πr²h × 9 ...(ii)

समीकरण (i) व समीकरण (ii) से
\(\frac{1}{3}\)πr²h × 9 = 48 π
या 3r = 48
या r² = \(\frac{48}{3}\)
∴ r = \(\sqrt{16}\) = 4 cm
∴ आधार का व्यास (2r)= 2 × 4 = 8 cm उत्तर

प्रश्न 5.
ऊपरी व्यास 3.5 m वाले शंकु के आकार का एक गढ्ढा 12 m गहरा है। इसकी धारिता किलोलीटरों में कितनी है?
हल:
शंकु के आकार के गड्ढे का व्यास
= 3.5 m
∴ गड्ढे की त्रिज्या (r) = \(\frac{3.5}{2}\) = 1.75 m
गड्ढे की गहराई (h) = 12 m

∴ गड्ढे की धारिता = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3} \times \frac{22}{7}\) × 1.75 × 1.75 × 12
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{175}{100} \times \frac{175}{100}\) × 12
= \(\frac{1}{3} \times \frac{22}{7} \times \frac{7}{4} \times \frac{7}{4}\) × 12
= 22 × \(\frac{7}{4}\) = 11 × \(\frac{7}{2}\)
= \(\frac{77}{2}\) m³
= 38.5 m³
= 38.5 kl.
(∵ 1 m = 1000 1 = 1 kl)

प्रश्न 6.
एक लम्ब वृत्तीय शंकु का आयतन 9856 cm है। यदि इसके आधार का व्यास 28 cm है, तो ज्ञात कीजिए
(i) शंकु की ऊँचाई
(ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल।
हल:
(i) प्रश्नानुसार शंकु का आयतन
= 9856 cm शंकु के आधार का व्यास (2r) = 28 cm
आधार की त्रिज्या (r) = 28 = 14 cm

माना कि शंकु की ऊँचाई h है।
∴ \(\frac{1}{3}\)πr²h = 9856 [∵ शंकु का आयतन = \(\frac{1}{3}\)πr²h]
या \(\frac{1}{3} \times \frac{22}{7}\) × 14 × 14 × h = 9856
या \(\frac{1}{3}\) × 22 × 2 × 14 × h = 9856
या h = \(\frac{9856 \times 3}{22 \times 2 \times 14}\)
∴ h = 48 cm

(ii) माना कि शंकु की तिर्यक ऊँचाई । है। अत:
l² = r² + h²
या l = (14)² + (48)²
= 196 + 2304
= 2500
l = 2500
= 50 cm

(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 14 × 50
= 2200 cm

प्रश्न 7.
भुजाओं 5 cm, 12 cm और 13 cm वाले एक समकोण त्रिभुज ABC को भुजा 12 cm के परित घुमाया जाता है। इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए।
हल:
जब भुजाओं 5 cm, 12 cm तथा 13 cm वाले एक समकोण 13 cm त्रिभुज ABC को इसकी भुजा 12 cm वाली भजा के परित घुमाया जाता है तो एक ठोस शंक्वाकार आकृति प्राप्त होती है।

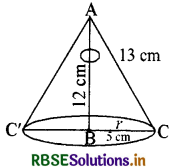
इस प्रश्न के अनुसार 12 cm वाली भुजा शंकु की ऊँचाई तथा 5 cm भुजा शंकु के आधार की त्रिज्या होगी।
यहाँ शंकु की त्रिज्या (r) = 5 cm
शंकु की ऊँचाई (h) = 12 cm

शंकु का आयतन = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × π × 5 × 5 × 12
= 100 m cm

प्रश्न 8.
यदि प्रश्न 7 के त्रिभुज ABC को यदि भुजा 5 cm के परित घुमाया जाए, तो इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए। प्रश्नों 7 और 8 में प्राप्त किए गए दोनों ठोसों के आयतनों का अनुपात भी ज्ञात कीजिए।
हल:
प्रश्नानुसार यदि समकोण त्रिभुज को 5 cm भुजा के परित घुमाया जाता है तो ठोस शंक्वाकार आकृति प्राप्त होती है।

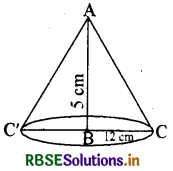
अब यहाँ 5cm वाली भुजा शंकु के आधार की त्रिज्या तथा 5 cm वाली भुजा शंकु की ऊँचाई होती है। अब यहाँ R = 12 cm शंकु की त्रिज्या तथा H = 5 cm शंकु की ऊँचाई है।
शंकु का आयतन = \(\frac{1}{3}\)πR²h
= \(\frac{1}{3}\) × π × 12 × 12 × 5
= 240 π cm

अब प्रश्नानुसार

= \(\frac{100 \pi}{240 \pi}=\frac{5}{12}\)
∴ वांछनीय अनुपात = 5 : 12

प्रश्न 9.
गेहूँ की एक ढेरी 10.5 m व्यास और ऊँचाई 3 m वाले एक शंकु के आकार की है। इसका आयतन ज्ञात कीजिए। इस ढेरी को वर्षा से बचाने के लिए केनवास से ढका जाना है। वाँछित केनवास का क्षेत्रफल ज्ञात कीजिए।
हल:
माना कि गेहूँ की शंक्वाकार ढेरी के आधार की त्रिज्या r है। अतः
व्यास (2r) = 10.5 m
या r = \(\frac{10.5}{2}\) m
= \(\frac{105}{20}\) m
या r = \(\frac{21}{4}\) m
तथा शंक्वाकार ढेरी की ऊँचाई (h) = 3 m
इस गेहूँ की ढेरी का आयतन = \(\frac{1}{3}\)πr²h

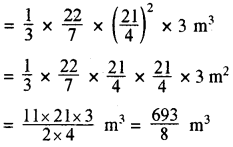
= 86.625 m³

अब माना कि शंकु के आकार की ढेरी की तिर्यक ऊँचाई | m है।
l² = r² + h²

या l² = \(\left(\frac{21}{4}\right)^{2}\) + (3)²
= \(\frac{441}{16}\) + 9
= \(\frac{441+144}{16}\)
या l² = \(\frac{585}{16}\)
= 36.5626 m
∴ l² = \(\sqrt{36.5626}\) m = 6.046 m
∴ वांछित केनवास का क्षेत्रफल = शंकु के वक्र पृष्ठ का क्षेत्रफल
= πrl
= \(\frac{22}{7} \times \frac{21}{4}\) × 6.046
= 99.75 m² (लगभग)