RBSE Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.7 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 13 Surface Areas and Volumes Ex 13.7

Question 1.
Find the volume of the right circular cone with :
(i) radius 6 cm, height 7 cm.
(ii) radius 3.5 cm, height 12 cm.
Answer:
(i) Here, r = 6 cm and h = 7 cm.
∴ Volume of the cone = \(\frac{1}{3}\)πr²h = (\(\frac{1}{3} \times \frac{22}{7}\) × 6 × 6 × 7) cm³ = 264 cm³.

(ii) Here, r = 3.5 cm and h = 12 cm.
∴ Volume of the cone = \(\frac{1}{3}\)πr²h = (\(\frac{1}{3} \times \frac{22}{7}\) × 3.5 × 3.5 × 12)cm³ = 154 cm³.

Question 2.
Find the capacity in litres of a conical vessel with :
(i) radius 7 cm, slant height 25 cm.
(ii) height 12 cm, slant height 13 cm.
Answer:
(i) Here, r = 7 cm and l = 25 cm.
Let the height of the cone be h cm.
Then, h² = l² - r² = 25² - 7² = 625 - 49 = 576
So, h = \(\sqrt{576}\) cm = 24 cm

Volume of the conical vessel = \(\frac{1}{3}\)πr²h
= (\(\frac{1}{3} \times \frac{22}{7}\) × 7 × 7 × 24) cm³ = 1232 cm³
∴ Capacity of the vessel in litres = \(\left(\frac{1232}{1000}\right)\) litres = 1232 litres.

(ii) Here, h = 12 cm and l = 13 cm.
Let the radius of the base of the cone be r cm.
Then, r² = l² - h² = 13² - 12²
= 169 - 144 = 25
So, r = \(\sqrt{25}\) cm = 5 cm

Volume of the conical vessel = \(\frac{1}{3}\)πr²h = (\(\frac{1}{3} \times \frac{22}{7}\) × 5 × 5 × 12) cm² = \(\frac{2200}{7} \)cm3
∴ Capacity of the vessel in litres = \(\left(\frac{2200}{7} \times \frac{1}{1000}\right)\) litres = \(\frac{11}{35}\)litres

Question 3.
The height of a cone is 15 cm. If its volume is 1570 cm³, find the radius of the base. (Use π = 3.14)
Answer:
Here, h = 15 cm and volume = 1570 cm³
Let the radius of the base of the cone be r cm.
Now, Volume = 1570 cm³
So, \(\frac{1}{3}\)πr²h = 1570 ⇒ \(\frac{1}{3}\) × 3.14 × r² × 15 = 1570
or r² = \(\frac{1570}{3.14 \times 5}\) = 100 ⇒ r = \(\sqrt{100}\) = 10
Thus, the radius of the base of the cone is 10 cm.

Question 4.
If the volume of a right circular cone of height 9 cm is 48 n cm³, find the diameter of its base.
Answer:
Here, h = 9 cm and volume = 48π cm3.
Let the radius of the base of the cone be r cm.
∴ Volume = 4871 cm3 ⇒ \(\frac{1}{3}\)πr²h = 48π
or \(\frac{1}{3}\) × r² × 9 = 48 ⇒ 3r² = 48
or r² = \(\frac{48}{3}\) = 16 ⇒ r = \(\sqrt{16}\) = 4
Thus, the diameter of the base of the cone is 2 × 4 cm, i.e. 8 cm.

Question 5.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Answer:
Diameter of the top of the conical pit = 3.5 m
∴ Radius = m = 1.75 m
Depth of the pit, i.e. height = 12 m
∴ Volume = \(\frac{1}{3}\)πr²h = (\(\frac{1}{3} \times \frac{22}{7}\) × 1.75 × 1.75 × 12) m³ = 38.5 m³
∴ Capacity of the pit = 38.5 kilolitres.

Question 6.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find :
(i) height of the cone,
(ii) slant height of the cone,
(iii) curved surface area of the cone.
Answer:
(i) Diameter of the base of the cone = 28 cm
∴ Radius = r = \(\left(\frac{28}{2}\right)\) cm = 14 cm.
Volume of the cone = 9856 cm³

Let the height of the cone be h cm.
Now, volume = 9856 cm3 ⇒ \(\frac{1}{3}\)πr²h = 9856
or \(\frac{1}{3} \times \frac{22}{7}\) × 14 × 14 × h = 9856 or h = \(\frac{9856 \times 3 \times 7}{22 \times 14 \times 14}\) = 48
Thus, the height of the cone is 48 cm.

(ii) Here, r = 14 m and h = 48 cm.
Let l be the slant height of the cone.
Then, l² = h² + r² = 48² + 14² = 2304 + 196 = 2500
So, l = \(\sqrt{2500}\) cm = 50 cm
Thus, the slant height of the cone is 50 cm.

(iii) Here, r = 14 cm and l = 50 cm.
∴ Curved surface area = πrl = (\(\frac{22}{7}\) × 14 × 50) cm = 2200 cm

Question 7.
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Answer:

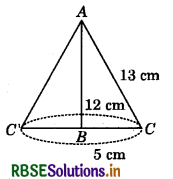
On revolving the right ∆ABC about the side AB (= 12 cm), we get a cone as shown in the figure.
Volume of solid so obtained = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\)× π × 12 × 12 × 5 cm³
= 100π cm³

Question 8.
If the triangle ABC in question. 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Answer:

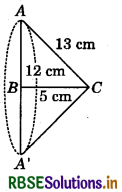
On revolving the right AABC about the side BC (= 5 cm), we get a cone as shown in the figure.
Volume of solid so obtained = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × π × 12 × 12 × 5 cm³ = 240π cm³
∴ Ratio of their volumes = 100π: 240π
= 5 : 12.

Question 9.
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
Answer:
Diameter of the base of the cone = 10.5 m
∴ Radius = r = \(\left(\frac{10.5}{2}\right)\)m = 5.25 m
Height of the cone = 3m
∴ Volume of the cone (heap) = \(\frac{1}{3}\)πr2h = (\(\frac{1}{3} \times \frac{22}{7}\) × 5.25 × 5.25 × 3) m³
= 86.625 m³
To find the slant height l:
We have l² = h² + r² = 3² + (5.25)² = 9 + 27.5625 = 36.5625
⇒ l = 736.5625 m = 6.0467 m = 6.05 (approx.)
Canvas required to protect wheat from rain = Curved surface area
= πrl = (\(\frac{22}{7}\) × 5.25 × 6.05 = 99.825 m² (approx.)