RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3

जब तक अन्यथा न कहा जाए, π = \(\frac{22}{7}\) लीजिए।

Class 9 Maths Exercise 13.3 Solutions Hindi Medium प्रश्न 1.
एक शंकु के आधार का व्यास 10.5 cm है और इसकी तिर्यक ऊँचाई 10 cm है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
माना कि शंकु के वृत्ताकार आधार की त्रिज्या r cm है।

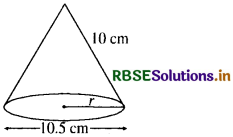
प्रश्नानुसार व्यास (2r) = 10.5 cm
∴ r = \(\frac{10.5}{2}\) cm
या  r = \(\frac{105}{2}\) cm
या r = \(\frac{21}{4}\) cm
शंकु की तिर्यक ऊँचाई (l) = 10 cm
हम जानते हैं कि शंकु का वक्र पृष्ठीय क्षेत्रफल
= πrl
= \(\frac{22}{7} \times \frac{21}{4} \times 10\)
= 165 cm²

13.3 Class 9 In Hindi प्रश्न 2.
एक शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 21 m है और आधार का व्यास 24 m है।
हल:
प्रश्नानुसार शंकु की तिर्यक
ऊँचाई (l) = 21 m
शंकु का व्यास (2r) = 24 m
∴ r = \(\frac{24}{2}\) = 12 m

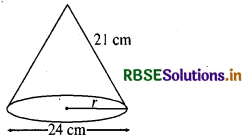
हम जानते हैं कि शंकु का कुल पृष्ठीय क्षेत्रफल
= πrl + πr²
= πr(l + r)
= \(\frac{22}{7}\) × 12(21 + 12) m²
= \(\frac{22}{7}\) × 12 × 33 m²
= 1244.57 m². 

Class 9 Math Chapter 13.3 Hindi Medium प्रश्न 3.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 cm है और इसकी तिर्यक ऊँचाई 14 cm है। ज्ञात कीजिए
(i) आधार की त्रिज्या
(ii) शंकु का कुल पृष्ठीय क्षेत्रफल।
हल:
(i) प्रश्नानुसार शंकु के वक्र पृष्ठ का क्षेत्रफल = 308 cm
शंकु की तिर्यक ऊँचाई (l) = 14 cm
माना कि शंकु के वृत्ताकार भाग के आधार की त्रिज्या r cm है।
हम जानते हैं कि शंकु के वक्र पृष्ठ का क्षेत्रफल = πrl
अर्थात् πrl = 308
या \(\frac{22}{7}\) × r × 14 = 308
r = 308 × \(\frac{7}{22}\) × \(\frac{1}{14}\)
r = 7 cm 

(ii) हम जानते हैं कि शंकु का कुल पृष्ठीय क्षेत्रफल = शंकु के वक्र पृष्ठ का क्षेत्रफल + शंकु के वृत्ताकार भाग का क्षेत्रफल
= πrl + πr²
= 308 + \(\frac{22}{7}\) × (7)²
= 308 + \(\frac{22}{7}\) × 7 × 7
= 308 + 154
= 462 cm² 

Class 9 Maths Chapter 13.3 In Hindi प्रश्न 4.
शंकु के आकार का एक तम्ब 10 m ऊँचा है और उसके आधार की त्रिज्या 24 m है। ज्ञात कीजिए
(i) तम्बू की तिर्यक ऊँचाई।
(ii) तम्बू में लगे केनवास (canvas) की लागत, यदि 1 m केनवास की लागत 70 रुपये है।
हल:
(i) प्रश्नानुसार शंकु के आकार के तम्बू की ऊँचाई (1) = 10 m
तथा शंक्वाकार तम्बू के आधार की त्रिज्या
(r) = 24 m
हम जानते हैं कि तम्बू की तिर्यक ऊँचाई

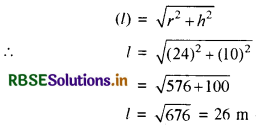
(ii) तम्बू में लगे केनवास का क्षेत्रफल = तम्बू के वक्र पृष्ठ का क्षेत्रफल
= πrl 
= \(\frac{22}{7}\) × 24 × 26 
= \(\frac{13728}{7}\) m²
∵ 1 m² केनवास की लागत = 70 रु.
∵ \(\frac{13728}{7}\) m² केनवास की लागत
= 70 × \(\frac{13728}{7}\) रु.
= 137280 रु. 

Class 9 Maths Chapter 13 Exercise 13.3 In Hindi प्रश्न 5.
8 m ऊँचाई और आधार की त्रिज्या 6 m वाले एक शंकु के आकार का तम्बू बनाने में 3 m चौड़े तिरपाल की कितनी लम्बाई लगेगी? यह मानकर चलिए कि इसकी सिलाई और कटाई में 20 cm तिरपाल अतिरिक्त लगेगा। (π = 3.14 का प्रयोग कीजिए।)
हल:
प्रश्नानुसार तम्बू की ऊँचाई (h) = 8 m,
तम्बू के आधार की त्रिज्या (r) = 6 m
अतः तम्बू की तिर्यक ऊँचाई (I) = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{(6)^{2}+(8)^{2}}\)
= \(\sqrt{36+64}\)
= \(\sqrt{100}\)
∴ l = 10 m
तम्बू में लगी तिरपाल का क्षेत्रफल = तम्बू के वक्र पृष्ठ का क्षेत्रफल
= πrl
= 3.14 × 6 × 10
= 188.4 m²
माना कि तिरपाल की लम्बाई (L) हो तथा प्रश्नानुसार तिरपाल की चौड़ाई = 3 m है। अतः
तिरपाल का क्षेत्रफल = लम्बाई × चौड़ाई
= L × 3 = 3L m
अतः 3L = 188.4
(∵ क्षेत्रफल = 188.4 m²)
∴ L = \(\frac{188.4}{3}\) = 62.8 m
प्रश्नानुसार सिलाई तथा कटाई में लगी तिरपाल की अतिरिक्त लम्बाई = 20cm = \(\frac{20}{100}\) m = 0.2 m
अतः तम्बू बनाने में लगी तिरपाल की कुल लम्बाई
= 62.8 + 0.2 m
= 63 m 

Exercise 13.3 Class 9 In Hindi प्रश्न 6.
शंकु के आकार की एक गुम्बज की तिर्यक ऊँचाई और आधार व्यास क्रमश: 25 m और 14 m है। इसकी वक्र पृष्ठ पर 210 रुपये प्रति 100 m- की दर से सफेदी कराने का व्यय ज्ञात कीजिए।
हल:
प्रश्नानुसार शंकु के आकार की गुम्बज की तिर्यक ऊँचाई
= l = 25 m
तथा आधार का व्यास (2r) = 14 m
∴ आधार की त्रिज्या (r) = \(\frac{14}{2}\) m = 7 m
अतः गुम्बज के वक्रपृष्ठ का क्षेत्रफल = πrl
= \(\frac{22}{7}\) × 7 × 25
= 550 m²
∵ 100 m² पर सफेदी कराने का व्यय = 210 रु.
∴ 1 m² पर सफेदी कराने का व्यय = 1
∴ 550 m² पर सफेदी कराने का व्यय
= \(\frac{210}{100}\) × 550 रु.
= 1155 रु.
अत: गुम्बज के वक्र पृष्ठ पर सफेदी कराने का व्यय = 1155 रु. 

Class 9 Maths Exercise 13.3 Solutions In Hindi प्रश्न 7.
एक जोकर की टोपी एक शंकु के आकार की है, जिसके आधार की त्रिज्या 7 cm और ऊँचाई 24 cm है। इसी प्रकार की 10 टोपियाँ बनाने के लिए आवश्यक गत्ते का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार शंक्वाकार टोपी के आधार की त्रिज्या (r) = 7 cm
टोपी की ऊँचाई (h) = 24 cm
अत: टोपी की तिर्यक ऊँचाई (l) = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{(7)^{2}+(24)^{2}}\) 
= \(\sqrt{49+576}\)
= √625
= 25 cm
एक टोपी बनाने में लगे गत्ते का क्षेत्रफल = शंकु का वक्र पृष्ठीय क्षेत्रफल
= πrl 
=  \(\frac{22}{7}\) × 7 × 25
= 550 cm²
अत: 10 टोपियाँ बनाने में लगे गत्ते का क्षेत्रफल
= 10 × 550
= 5500 cm²

Math Class 9 Chapter 13.3 In Hindi प्रश्न 8.
किसी बस स्टाप को पुराने गत्ते से बने 50 खोखले शंकुओं द्वारा सड़क से अलग किया हुआ है। प्रत्येक शंकु के आधार का व्यास 40 cm है और ऊँचाई 1 m है। यदि इन शंकओं की बाहरी पृष्ठों को पेंट करवाना है और पेंट की दर 12 रुपये प्रति m² है, तो इनको पेंट कराने में कितनी लागत आएगी? (π = 3.14 और √1.04 = 1.02 का प्रयोग कीजिए।)
हल:
माना कि वृत्ताकार आधार की त्रिज्या r cm है।
प्रश्नानुसार शंकु के आधार का व्यास (2r) = 40 cm
∴ r = \(\frac{40}{2}\) = 20 cm
या r = \(\frac{20}{100}\) = \(\frac{1}{5}\) m = 0.2 m
शंकु की ऊँचाई (h) = 1 m
∴ तिर्यक ऊँचाई (1) = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{(0.2)^{2}+(1)^{2}}\)
या l = \(\sqrt{0.04+1}\)
= √1.04 m = 1.02 m
अब शंकु के वक्र पृष्ठ का क्षेत्रफल = πrl
= 3.14 × 0.2 × 1.02
= 0.64056 m²
∵ 1 m² क्षेत्रफल को पेन्ट कराने की लागत = 12 रु.
∴ 0.64056 m² क्षेत्रफल को पेन्ट कराने की लागत
· = 12 × 0.64056
= 7.68672 रु.
अतः ऐसे ही 50 शंकुओं को पेन्ट कराने की लागत
= 50 × 7.68672 रु.
= 384.34 रु. (लगभग)
अतः शंकुओं पर सफेदी कराने में लगभग 384.34 रुपये व्यय होंगे।