RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2

प्रश्न 1.
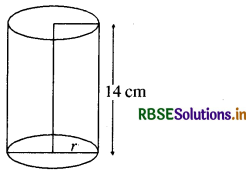
ऊँचाई 14 cm वाले एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 cm² है। बेलन के आधार का व्यास ज्ञात कीजिए।
हल:
माना कि लम्ब वृत्तीय बेलन के आधार की त्रिज्या r cm है।
प्रश्नानुसार बेलन की ऊँचाई (h) = 14 cm
बेलन का वक्रपृष्ठीय क्षेत्रफल = 88 cm
हम जानते हैं कि बेलन के वक्र पृष्ठ का क्षेत्रफल = 2πrh
अर्थात् 2πrh = 88
या 2 × \(\frac{22}{7}\) × r × 14 = 88

या 2 × 22 × r × 2 = 88
या r = \(\frac{88}{2 \times 22 \times 2}\)
अतः बेलन के आधार का व्यास = 2r
= 2 × 1 = 2 cm

प्रश्न 2.
धातु की एक चादर से 1 m ऊँची और 140 cm व्यास के आधार वाली एक बन्द बेलनाकार टंकी बनाई जानी है। इस कार्य के लिए कितने वर्ग मीटर चादर की आवश्यकता होगी?
हल:
माना कि धातु की चद्दर से बनी बेलनाकार टंकी के आधार की त्रिज्या r cm है।
∴ व्यास = 2r = 140 cm
या r = \(\frac{140}{2}\) = 70 cm
= \(\frac{70}{100}\)m = 0.7 m
अर्थात् (r) = 0.7 m
बेलन की ऊँचाई (h) = 1 m
अत: बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr(r + h)
= 2 × \(\frac{22}{7}\) × 0.7(0.7 + 1)
= 2 × \(\frac{22}{7}\) × \(\frac{7}{10}\) × 1.7
= 2 × 22 × \(\frac{1.7}{10}\)
= 7.48 m²
अतः कुल आवश्यक चादर = 7.48 m²

प्रश्न 3.
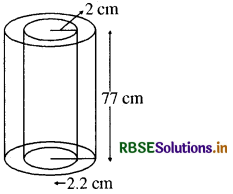
धातु का एक पाइप 77 cm लम्बा है। इसके एक अनुप्रस्थ काट का आन्तरिक व्यास 4 cm है और बाहरी व्यास 4.4 cm है (देखिए आकृति)।
ज्ञात कीजिए-

(i) आन्तरिक वक्र पृष्ठीय क्षेत्रफल
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल
(iii) कुल पृष्ठीय क्षेत्रफल।
हल:
(i) धातु के पाइप की लम्बाई = 77 cm
अनुप्रस्थ काट का आन्तरिक व्यास = 4 cm
अतः आन्तरिक त्रिज्या (r) = \(\frac{4}{2}\) = 2 cm

बेलनाकार पाइप के आन्तरिक वक्र पृष्ठ का क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) × 2 × 77
= 2 × 22 × 2 × 11
= 968 cm²

(ii) धातु के पाइप की लम्बाई = 77 cm
पाइप का बाहरी व्यास = 4.4 cm
∴ बाहरी त्रिज्या (r) = \(\frac{4.4}{2}\) = 2.2 cm
∴ बेलनाकार पाइप के बाहरी वक्र पृष्ठ का क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) × 2.2 × 77
= \(\frac{44}{7}\) × \(\frac{22}{10}\) × 77
= 44 × \(\frac{22}{10}\) × 11
= 1064.8 cm²

(iii) चूँकि पाइप के दोनों अंत सिरों में से प्रत्येक सिरे पर 2 cm तथा 2.2 cm त्रिज्याओं के वृत्त हैं । अतः पाइप के दोनों सिरों का क्षेत्रफल
= 2 (बाहरी वृत्त का क्षेत्रफल - आन्तरिक वृत्त का क्षेत्रफल)
= 2(πr₁² - πr₂²)
= 2π(r₁² - r₂²)
= 2 × \(\frac{22}{7}\) [(2.2)² - (2)²]
= 2 × \(\frac{22}{7}\) × [4.84 - 4]
= 2 × \(\frac{22}{7}\) × 0.84
= 5.28 cm
∴ धातु के पाइप का कुल पृष्ठीय क्षेत्रफल = आन्तरिक वक्र पृष्ठीय क्षेत्रफल + बाहरी वक्र पृष्ठीय क्षेत्रफल + दो वृत्तीय सिरों का क्षेत्रफल
= 968 cm² + 1064.8 cm² + 5.28 cm²
= 2038.08 cm²

प्रश्न 4.
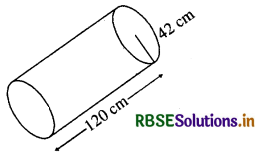
एक रोलर (roller) का व्यास 84 cm है और लम्बाई 120 cm है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का m- में क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार रोलर का व्यास = 84 cm
∴ त्रिज्या (r) = \(\frac{84}{2}\) = 42 cm
रोलर की लम्बाई (l) = 120 cm

बेलनाकार रोलर का वक्र पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल
= 2πrh [यहाँ बेलन की लम्बाई (l) = h]
= 2 × \(\frac{22}{7}\) × 42 × 120 = 2 × 22 × 6 × 120
= 31680 cm²
= \(\frac{31680}{100 \times 100}\) m²
= 3.1680 m²
अर्थात् एक चक्कर में रोलर द्वारा समतल किया जा सकने वाला क्षेत्रफल
= 3.1680 m²
अत: 500 चक्करों में समतल किया गया क्षेत्रफल
= 500 × 3.1680 m²
= 1584.0000 m²
= 1584 m²
यहाँ खेल के मैदान का क्षेत्रफल वही होगा जो रोलर द्वारा 500 चक्करों में समतल किया गया क्षेत्रफल है अर्थात् मैदान का क्षेत्रफल = 1584 m²

प्रश्न 5.
किसी बेलनाकार स्तम्भ का व्यास 50 cm है और ऊँचाई 3.5 m है। 12.50 रुपये प्रति m² की दर से इस स्तम्भ के वक्र पृष्ठ पर पेंट कराने का व्यय ज्ञात कीजिए।
हल:
प्रश्नानुसार स्तम्भाकार बेलन का व्यास = 50 cm
∴ स्तम्भ की त्रिज्या (r) = \(\frac{50}{2}\) = 25 cm
= \(\frac{25}{100}\) m = \(\frac{1}{4}\)m
स्तम्भ की ऊँचाई (h) = 3.5 m
अत: बेलनाकार स्तम्भ का पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{1}{4}\) × 3.5
= 2 × \(\frac{22}{7}\) × \(\frac{1}{4}\) × \(\frac{35}{10}\)
= \(\frac{11}{2}\) m²
∵ 1 m² पेन्ट कराने का व्यय = 12.50 रु.
∴ \(\frac{11}{2}\) m पेन्ट कराने का व्यय = 12.50 × \(\frac{11}{2}\)
= 68.75 रु.

प्रश्न 6.
एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m² है। यदि बेलन के आधार की त्रिज्या 0.7 m है, तो उसकी ऊँचाई ज्ञात कीजिए।
हल:
प्रश्नानुसार लम्ब वृत्तीय बेलन के वक्र पृष्ठ का क्षेत्रफल = 4.4 m²
तथा बेलन की त्रिज्या (r) = 0.7 m
बेलन की ऊँचाई (h) = ?
माना कि बेलन की ऊँचाई = h
∴ 2πrh = 4.4 .
या 2 × \(\frac{22}{7}\) × 0.7 × h = 4.4
या 2 × \(\frac{22}{7}\) × \(\frac{7}{10}\) × h = 4.4
या \(\frac{44}{10}\) × h = 4.4
या h = \(\frac{4.4 \times 10}{44}\)
= \(\frac{44}{10} \times \frac{10}{1} \times \frac{1}{44}\)
h = 1 m
∴ बेलन की ऊँचाई = 1 m 

प्रश्न 7.
किसी वृत्ताकार कुएँ का आन्तरिक व्यास 3.5 . m है और यह 10 m गहरा है। ज्ञात कीजिए
(i) आन्तरिक वक्र पृष्ठीय क्षेत्रफल।
(ii) 40 रु. प्रति m- की दर से इसके वक्र पृष्ठ पर प्लास्टर कराने का व्यय।
हल:
प्रश्नानुसार वृत्ताकार कुएँ का आन्तरिक व्यास = 3.5 m
∴ कुएँ की त्रिज्या (7) = \(\frac{3.5}{2}\) = 1.75 m
कुएँ की गहराई (h) = 10 m
(i) चूँकि कुआँ बेलनाकार है, अतः कुएँ का आन्तरिक वक्र पृष्ठ का क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) x 1.75 x 10 m²
= 2 × \(\frac{22}{7}\).× \(\frac{175}{100}\) × 10 m²
= 110 m² 

(ii) ∵ 1 m क्षेत्रफल पर प्लास्टर कराने का व्यय = 40रु.
∴ 110 m² पर प्लास्टर कराने का व्यय
= 40 × 110 रु.
= 4400 रु.

प्रश्न 8.
गरम पानी द्वारा गरम रखने वाले एक संयंत्र में 28 m लम्बाई और 5 cm व्यास वाला एक बेलनाकार पाइप है। इस संयंत्र में गर्मी देने वाला कुल कितना पृष्ठ है? हल:
माना कि बेलनाकार पाइप की लम्बाई (ऊँचाई) = h है।
प्रश्नानुसार h = 28 m.
तथा बेलनाकार पाइप की त्रिज्या (r) = r
प्रश्नानुसार 2r = 5 cm
या r = \(\frac{5}{2}\) cm
∴ गर्मी देने वाले बेलनाकार पाइप का वक्रपृष्ठीय | क्षेत्रफल = 2urh
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\) × 2800
= 44000 cm^{2
= \(\frac{44000}{10000}\)} m² [∵ 1 cm = \(\frac{1}{100}\)m]
[∴ 1 cm² = \(\frac{1}{10000}\) m²]
= 4.4 m²

प्रश्न 9.
ज्ञात कीजिए
(i) एक बेलनाकार पेट्रोल की बन्द टंकी का पार्श्व या वक्र पृष्ठीय क्षेत्रफल, जिसका व्यास 4.2 m है और ऊँचाई 4.5 m है।
(ii) इस टंकी को बनाने में कुल कितना इस्पात (steel) लगा होगा, यदि कुल इस्पात का 1 भाग बनाने में नष्ट हो गया है?
हल:
(i) प्रश्नानुसार बेलनाकार पेट्रोल की टंकी का व्यास
2r = 4.2 m
∴ त्रिज्या (r) = \(\frac{4.2}{2}\) = 2.1 m
टंकी की ऊँचाई (h) = 4.5 m
अतः पेट्रोल की टंकी का वक्र पृष्ठीय क्षेत्रफल
= 2πrh
= 2 × \(\frac{22}{7}\) × 2.1 × 4.5 m²
= 59.4 m² 

(ii) टंकी का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 2.1 (4.5 + 2.1)
= 2 × \(\frac{22}{7}\) × 0.3 × 6.6
= 87.12 m²
माना टंकी को बनाने में x m-इस्पात लगा
प्रश्नानुसार क्योंकि टंकी को बनाने में कुल इस्पात का \(\frac{1}{12}\) भाग नष्ट हो जाता है। अतः टंकी में लगे इस्पात का क्षेत्रफल
= x - \(\frac{1}{12}\)x = \(\frac{11}{12}\)x
प्रश्नानुसार \(\frac{11}{12}\)x = 87.12
⇒ x = \(\frac{87.12 \times 12}{11}\)
x = 95.04 m²
अतः टंकी को बनाने में लगा इस्पात = 95.04 m²

प्रश्न 10.
दी गयी आकृति में, आप एक लैंपशेड का फ्रेम देख रहे हैं। इसे एक सजावटी कपड़े से ढका जाना है। इस फ्रेम के आधार का व्यास 20 cm है और ऊँचाई 30 cm है। फ्रेम के ऊपर और नीचे मोड़ने के लिए दोनों ओर 2.5 cm अतिरिक्त कपड़ा भी छोड़ा जाना है। ज्ञात कीजिए कि लैंपशेड को ढकने के लिए कुल कितने कपड़े की आवश्यकता होगी?

हल:
फ्रेम की ऊँचाई (h) = 30 cm
ऊपर व नीचे मोड़े जाने वाले प्रत्येक कपड़े की ऊँचाई (h) = 2.5 cm
अब माना कि प्रत्येक भाग की त्रिज्या (r)
प्रश्नानुसार व्यास (2r) = 20 cm
या r = \(\frac{20}{2}\) cm = 10 cm
∵ लैंपशेड को सजाने. में दोनों ओर 2.5 सेमी. कपड़ा अतिरिक्त छोड़ा जाता है।
∴ अतिरिक्त कपड़े सहित कपड़े की ऊँचाई h
. = (30 + 2.5 + 2.5)
= 35 cm
आवश्यक कपड़े का क्षेत्रफल = 2πrh
= 2 × \(\frac{22}{7}\) × 10 × 35
= 2 × 22 × 10 × 5
= 2200 cm²
अतः आवश्यक कपड़ा = 2200 cm²

प्रश्न 11.
किसी विद्यालय के विद्यार्थियों से एक आधार वाले बेलनाकार कलमदानों को गत्ते से बनाने और सजाने की प्रतियोगिता में भाग लेने के लिए कहा गया। प्रत्येक कलमदान को 3 cm त्रिज्या और 10.5 cm ऊँचाई का होना था। विद्यालय को इसके लिए प्रतिभागियों को गत्ता देना था। यदि इसमें 35 प्रतिभागी थे, तो विद्यालय को कितना गत्ता खरीदना पड़ा होगा?
हल:
प्रश्नानुसार माना कि बेलनाकार कलमदान की त्रिज्या r है जो कि r = 3 cm है।
बेलनाकार कलमदान की ऊँचाई = h = 10.5 cm
कलमदान के लिए वांछित गत्ता = कलमदान का वक्रपृष्ठीय क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल
= 2πrh + πr²
= πr(2h + r)
= \(\frac{22}{7}\) × 3(2 × 10.5 + 3)
= \(\frac{22}{7}\) × 3(21 + 3)
= \(\frac{22}{7}\) × 3 × 24
= 226.28 cm²
अर्थात् प्रत्येक प्रतिभागी के लिए कलमदान बनाने के लिए वांछनीय गत्ते का क्षेत्रफल = 226.28 cm²
अतः 35 कलमदानों हेतु वांछित गत्ता
= (226.28 × 35) cm²
= 7919.8 cm²
= 7920 cm²