RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1

प्रश्न 1.
1.5 m लम्बा, 1.25 m चौड़ा और 65 cm गहरा प्लास्टिक का एक डिब्बा बनाया जाना है। इसे ऊपर से खुला रखना है। प्लास्टिक शीट की मोटाई को नगण्य मानते हुए, निर्धारित कीजिए-
(i) डिब्बा बनाने के लिए आवश्यक प्लास्टिक शीट का क्षेत्रफल।
(ii) इस शीट का मूल्य, यदि 1 m शीट का मूल्य 20 रुपये है।
हल:
प्रश्नानुसार चित्रांकन करने पर

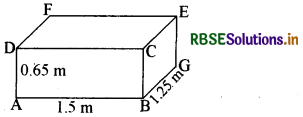
प्लास्टिक शीट की लम्बाई (l) = 1.5 m
चौड़ाई (b) = 1.25 m
तथा गहराई (h) = 65 cm
= \(\frac{65}{100}\) m = 0.65 m

(i) ऊपर से खुले हुए वांछित बॉक्स की (शीट का) क्षेत्रफल
= 2(bh + hl) + lb
= 2[1.25 × \(\frac{65}{100}\) + \(\frac{65}{100}\) × 1.5] + 1.5 × 1.25
= 2(0.8125 + 0.975) + 1.875
= 2(1.7875) + 1.875
= 3.575 + 1.875
= 5.45 m²

(ii) ∵ 1 m² शीट का मूल्य = 20 रु.
∴ 5.45 m' शीट का मूल्य
= (20 × 5.45) रु.
= 109 रु.

प्रश्न 2.
एक कमरे की लम्बाई, चौड़ाई और ऊँचाई क्रमश: 5m, 4m और 3 m है। 7.50 रुपये प्रति m2 की दर से इस कमरे की दीवारों और छत पर सफेदी कराने का व्यय ज्ञात कीजिए। हल:
प्रश्नानुसार कमरे की लम्बाई (1) = 5 m
चौड़ाई (b) = 4 m
तथा ऊँचाई (h) = 3 m
∵ कमरे की चारों दीवारों का क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल
= 2(bh + hl) = 2h(b + 1)
= 2(4 + 5) 3 = 2 × 9 × 3
= 54 m²
छत का क्षेत्रफल = l × b
= (5 × 4) m²
= 20 m²
अत: दीवारों तथा छत का कुल क्षेत्रफल
= 54 m² + 20 m²
= 74 m²
∵ 1 m² सफेदी कराने का व्यय = 7.50 रु.
∴ 74 m² सफेदी कराने का व्यय 
= (7.50 × 74) रु.
= 555 रु.

प्रश्न 3.
किसी आयताकार हॉल के फर्श का परिमाप 250 m है। यदि 10 रुपये प्रति m- की दर से चारों दीवारों पर पेंट कराने की लागत 15,000 रुपये है, तो इस हॉल की ऊँचाई ज्ञात कीजिए।
[संकेत: चारों डिब्बों का क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल]
हल:
माना कि आयताकार हॉल की लम्बाई = lm
तथा चौड़ाई = bm
∴ आयताकार हॉल के फर्श का परिमाप
= 2(l + b)
= 250 m ........ (1)
हाल की चार दीवारों का क्षेत्रफल

= \(\frac{15000}{10}\)
= 1500 m² .......(ii)
यह भी माना कि आयताकार हॉल की ऊँचाई = hm चार दीवारों का क्षेत्रफल = 2(l + b)h
या 1500 = 250 × h
या h = \(\frac{1500}{250}\) = 6 m
अत: हॉल की ऊँचाई = 6 m

प्रश्न 4.
किसी डिब्बे में भरा हुआ पेंट 9.375 m² के क्षेत्रफल पर पेंट करने के लिए पर्याप्त है। इस डिब्बे के पेंट से 22.5 cm × 10 cm × 7.5 cm विमाओं वाली कितनी ईंट पेंट की जा सकती हैं?
हल:
प्रश्नानुसार ईंट की लम्बाई (1) = 22.5 cm
चौड़ाई (b) = 10 cm
तथा ऊँचाई (h) = 7.5 cm
अब ईंट का क्षेत्रफल = 2(lb + bh + hl)
= 2(22.5 × 10 + 10 × 7.5 + 7.5 × 22.5) cm²
= 2(225 + 75 + 168.75) cm²
= 2(468.75) = 937.5 cm²
cm² को m² में बदलने पर
= 937.5 × \(\left(\frac{1}{100}\right)^{2}\) ∵ 1 cm = \(\frac{1}{100}\) m
= \(\frac{937.5}{10000}\) = 0.09375 m²
अतः पेन्ट की जाने वाली ईंटों की संख्या
9.375 m² क्षेत्रफल पेन्ट कराने के

प्रश्न 5.
एक घनाकार डिब्बे का एक किनारा 10 cm लम्बाई का है तथा एक अन्य घनाभाकार डिब्बे की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 12.5 cm, 10 cm और 8 cm है।
(i) किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना कम है?
हल:
माना कि घनाकार डिब्बे का एक किनारा
= l = 10 cm

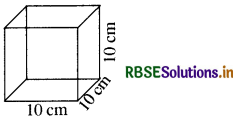
(i) घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल
= डिब्बे की चारों दीवारों का क्षेत्रफल
= 4l²
= 4(10)l²
= 4 × (10 × 10) = 400 cm .....(i)
अब पुनः माना कि घनाभाकार डिब्बे की लम्बाई
= l = 12.5 cm
चौड़ाई = 10 cm
तथा ऊँचाई = 8 cm

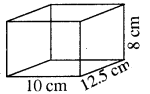
अब घनाभाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = इसकी चारों दीवारों का क्षेत्रफल
= 2(l + b) × h
= 2(12.5 + 10) × 8
= 2(22.5) × 8 = 360 cm .....(ii)
समीकरण (i) व (ii) के आधार पर यह कहा जा सकता है कि घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल घनाकार डिब्बे से 400 cm² - 360 cm² = 40 cm² अधिक है।
(ii) प्रश्नानुसार घनाकार डिब्बे का कुल क्षेत्रफल
= 6l²
= 6(10)²
= 6 × 100
= 600 cm² .....(iii)
तथा घनाभाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल
= 2(lb + bh + hl)
= 2(10 × 12.5 + 12.5 × 8 + 8 × 10)
= 2(125 + 100 + 80)
= 2(305)
= 610 cm² .....(iv)
समीकरण (iii) व (iv) के आधार पर यह कहा जा सकता है कि घनाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल घनाभाकार डिब्बे के पृष्ठीय क्षेत्रफल से 610 cm² - 600 cm² = 10 cm² कम है।

प्रश्न 6.
एक छोटा पौधा घर (green house) सम्पूर्ण रूप से शीशे की पट्टियों से (आधार भी सम्मिलित है) घर के अन्दर ही बनाया गया है और शीशे की पट्टियों को टेप द्वारा चिपका कर रोका गया है। यह पौधा घर 30 cm लम्बा, 25 cm चौड़ा और 25 cm ऊँचा है।
(i) इसमें प्रयुक्त शीशे की पट्टियों का क्षेत्रफल क्या है?
(ii) सभी 12 किनारों के लिए कितने टेप की आवश्यकता है?
हल:
(i) प्रश्नानुसार माना कि पौधा घर की लम्बाई
(l) = 30 cm
चौड़ाई (b) = 25 cm
तथा ऊँचाई (h) = 25 cm
पौधाघर में प्रयुक्त शीशे की पट्टियों का क्षेत्रफल
= 2(lb + bh + hl)
= 2(30 × 25 + 25 × 25 + 25 × 30)
= 2(750 + 625 + 750)

= 2(2125)
= 4250 cm²
(ii) सभी 12 किनारों पर प्रयुक्त टेप की कुल लम्बाई
= 4(l + b + h)
= 4(30 + 25 + 25)
= 4(80) cm
= 320 cm

प्रश्न 7.
शान्ति स्वीट स्टाल अपनी मिठाइयों को पैक करने के लिए गत्ते के डिब्बे बनाने का ऑर्डर दे रहा था। दो मापों के डिब्बों की आवश्यकता थी। बड़े डिब्बों की माप 25 cm × 20 cm × 5 cm और छोटे डिब्बों की माप 15 cm × 12 cm × 5 cm थीं। सभी प्रकार की अतिव्यापिकता (overlaps) के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर अतिरिक्त गत्ता लगेगा। यदि गत्ते की लागत 4 रुपये प्रति 1000 cm² है, तो प्रत्येक प्रकार के 250 डिब्बे बनवाने की कितनी लागत आएगी?
हल:
माना कि बड़े डिब्बे की लम्बाई (1) = 25 cm
चौड़ाई (b) = 20 cm
तथा ऊँचाई (h) = 5 cm

अत: बड़े डिब्बे का पृष्ठीय क्षेत्रफल
= 2(lb + bh + hl)
= 2(25 × 20 + 20 × 5 + 5 × 25) cm²
= 2(500 + 100 + 125) cm²
= 2(725) cm²
= 1450 cm²
सभी प्रकार की अति व्यापिकता के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर वांछनीय गत्ते का क्षेत्रफल
= 1450 का 5%
= 1450 × \(\frac{5}{100}\)
= 72.5 cm²
इस प्रकार कुल क्षेत्रफल = (1450 + 72.5) cm²
= 1522.5 cm²
इसी क्षेत्रफल के 250 डिब्बों का सम्पूर्ण क्षेत्रफल
= (1522.5 × 250) cm
= 380625 cm²
∵1000 cm² गत्ते की लागत = 4 रु.
∴ 1 cm² गत्ते की लागत = \(\frac{4}{1000}\) रु.
∴ 380625 cm- गत्ते की लागत
= \(\frac{4}{1000}\) × 380625
= 1522.50 रु.
अब पुनः माना कि छोटे डिब्बे की लम्बाई
(l) = 15 cm
चौड़ाई (b) = 12 cm
तथा ऊँचाई (h) = 5 cm

अतः छोटे डिब्बे का कुल पृष्ठीय क्षेत्रफल
= 2(lb + bh + hl)
= 2(15 × 12 + 12 × 5 + 5 × 15) cm²
= 2(180 + 60 + 75) cm²
= 2(315) cm²
= 630 cm²
सभी प्रकार की अतिव्यापिकता के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर वांछनीय गत्ते का क्षेत्रफल
= 630 का 5%
= 630 × \(\frac{5}{100}\) cm²
= 31.5 cm²
इस प्रकार कुल क्षेत्रफल = (630 + 31.5) cm²
= 661.5 cm²
इसी क्षेत्रफल के 250 डिब्बों का सम्पूर्ण क्षेत्रफल
= 661.50 × 250 cm²
= 165375 cm²
∵ 1000 cm² हेतु गत्ते की लागत = 4 रु.
∴ 1 cm² हेतु गत्ते की लागत = \(\frac{4}{1000}\) रु.
∴ 165375 cm² हेतु गत्ते की लागत
= \(\frac{4}{1000}\) × 165375 रु.
= 661.5 रु.
इस प्रकार प्रत्येक प्रकार के 250 गत्ते के डिब्बों की लागत
= 1522.5 रु. + 661.5 रु.
= 2184 रु.

प्रश्न 8.
परवीन अपनी कार खड़ी करने के लिए, एक सन्दूक के प्रकार के ढाँचे जैसा एक अस्थाई स्थान तिरपाल की सहायता से बनाना चाहती है, जो कार को चारों ओर से और ऊपर से ढक ले (सामने वाला फलक लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है)। यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा नगण्य होगा, आधार विमाओं 4 मीटर × 3 मीटर और ऊँचाई 2.5 मीटर वाले इस ढाँचे को बनाने के लिए कितने तिरपाल की आवश्यकता होगी?
हल:
माना कि आधार की लम्बाई (I) = 4 m
चौड़ाई (b) = 3 m
तथा ऊँचाई (h) = 2.5 m
कार खड़ी करने के लिए आवश्यक तिरपाल
= चार दीवारों का क्षेत्रफल + छत का क्षेत्रफल
= 2(l + b) h + lb
= 2(4 + 3) × 2.5 + 4 × 3 m²
= 2 × 7 × 2.5 + 12 m²
= 35 + 12 m²
= 47 m²