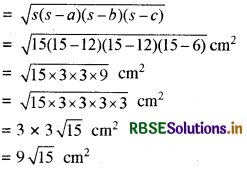RBSE Solutions for Class 9 Maths Chapter 12 हीरोन का सूत्र Ex 12.1

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 12 हीरोन का सूत्र Ex 12.1 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 12 हीरोन का सूत्र Ex 12.1

प्रश्न 1.
एक यातायात संकेत बोर्ड पर 'आगे स्कल है' लिखा है और यह भुजा 'a' वाले एक समबाहु त्रिभुज के आकार का है। हीरोन के सूत्र का प्रयोग करके इस बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि संकेत बोर्ड का परिमाप 180 cm है, तो इसका क्षेत्रफल क्या होगा?
हल:
यातायात संकेत बोर्ड 'a' भुजा वाले एक समबाहु त्रिभुज के आकार का है। माना कि यह ∆PQR . है। प्रश्नानुसार त्रिभुज PQR की प्रत्येक भुजा = a

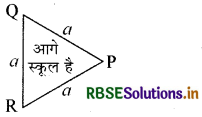
इस समबाहु त्रिभुज का परिमाप = a + a + a = 3a
तथा अर्द्ध-परिमाप (s) = \frac{3 a}{2}
हीरोन के अनुसार ∆PQR का क्षेत्रफल
= \(\sqrt{s(s-a)(s-b)(s-c)}\)

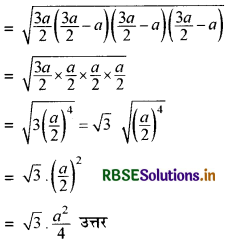
प्रश्नानुसार समबाहु त्रिभुज का परिमाप = 180 सेमी.
या a + a + a = 180 सेमी.
या 3a = 180 सेमी.
या a = 180 सेमी.
या a = 60 सेमी.
अतः त्रिभुज का क्षेत्रफल = √3.\(\frac{a^{2}}{4}\)
= √3.\(\frac{(60)^{2}}{4}\) सेमी².
= √3.\(\frac{3600}{4}\) सेमी².
= √3. 900 सेमी².
= 900√3 सेमी².
अतः बोर्ड का क्षेत्रफल = 900√3 सेमी.²

प्रश्न 2.
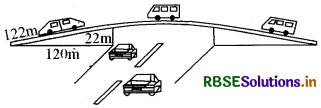
किसी फ्लाईओवर (flyover) की त्रिभुजाकार दीवार को विज्ञापनों के लिए प्रयोग किया जाता है। दीवार की भुजाओं की लम्बाइयाँ 122 m, 22 m और 120 m हैं ( देखिए आकृति)। इस विज्ञापन से प्रति वर्ष 5000 रु. प्रति m2 की प्राप्ति होती है। एक कम्पनी ने एक दीवार को विज्ञापन देने के लिए 3 महीने के लिए किराए पर लिया। उसने कुल कितना किराया दिया?

हल:
माना कि फ्लाईओवर की त्रिभुजाकार दीवार की भुजाएँ क्रमशः a, b तथा c हैं।
प्रश्नानुसार a = 122 m, b = 22 m तथा c = 120 m
त्रिभुज का परिमाप = (122 + 22 + 120) m
= 264 m
∴ अर्द्ध-परिमाप (s) = \(\frac{264}{2}\) = 132 m
हीरोन के सूत्र से इस त्रिभुज का क्षेत्रफल

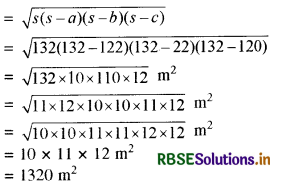
दीवार पर 1 वर्ष का विज्ञापन किराया
= 5,000 रु./m²
∴ दीवार पर 1 माह का विज्ञापन किराया
= \(\frac{5,000}{12}\) रु./m²
अतः दीवार पर 3 माह का विज्ञापन किराया
= \(\frac{5,000}{12}\) × 3 रु./m²
= \(\frac{5,000}{4}\) रु./m²
अर्थात् प्रति वर्ग मीटर विज्ञापन का किराया
= \(\frac{5,000}{4}\) रु
अतः 1320 m² का विज्ञापन किराया
= \(\frac{5,000}{4}\) × 1320 रु.
= 5,000 × 330 रु.
= 16,50,000 रु.
अत: कम्पनी द्वारा दिया गया किराया
= 16,50,000 रु.

प्रश्न 3.
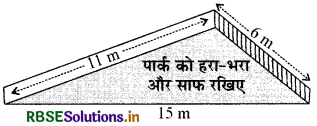
किसी पार्क में एक फिसल पट्टी (slide) बनी हुई है। इसकी पाश्र्वीय दीवारों (side walls) में से एक दीवार पर किसी रंग से पेंट किया गया है और उस पर "पार्क को हरा-भरा और साफ रखिए" लिखा हुआ है ( देखिए आकृति)। यदि इस दीवार की विमाएँ 15 m, 11 m और 6 m हैं, तो रंग से पेंट हुए भाग का क्षेत्रफल ज्ञात कीजिए।

हल:
प्रश्नानुसार रंग से पेंट की हुई त्रिभुजाकार दीवार की तीनों भुजाएँ क्रमश: 15 m, 11 m और 6 m हैं । अतः इस त्रिभुजाकार दीवार का परिमाप
= 15 + 11 + 6 = 32 m
त्रिभुज का अर्द्ध-परिमाप = \(\frac{32}{2}\) = 16 m
हीरोन के क्षेत्रफल के सूत्रानुसार

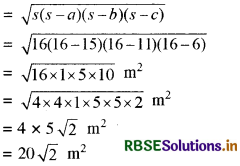
अतः पेन्ट किये हुये भाग का क्षेत्रफल
= 20√2 m²

प्रश्न 4.
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 cm और 10 cm हैं तथा उसका परिमाप 42 cm है।
हल:
प्रश्नानुसार त्रिभुज की दो भुजाएँ = 18 cm तथा 10 cm और परिमाप = 42 cm

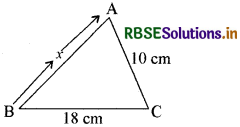
अर्थात् 18 cm + 10 cm + x = 42 cm
या 28 cm + x = 42 cm
या = 42 cm - 28 cm
यो x = 14 cm
∴ इस त्रिभुज का अर्द्ध-परिमाप
s = \(\frac{a+b+c}{2}\) = \(\frac{18+10+14}{2}\)
= \(\frac{42}{2}\) = 21 cm
हीरोन के सूत्र से इस त्रिभुज का क्षेत्रफल

अतः ∆ का क्षेत्रफल = 21√11 cm²

प्रश्न 5.
एक त्रिभुज की भुजाओं का अनुपात 12 : 17 : 25 है और उसका परिमाप 540 cm है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार त्रिभुज की भुजाओं का अनुपात = 12 : 17 : 25
माना कि अनुपात के आधार पर त्रिभुज की तीनों भुजाएँ क्रमश: 12x, 17x तथा 25x हैं।
त्रिभुज का परिमाप = 540 cm (दिया है)
या 12x + 17x + 25x = 540
या 54x = 540
या x = \(\frac{540}{54}\) = 10 cm
अतः त्रिभुज की भुजाएँ होंगी
12x = 12 × 10 = 120 cm
17x = 17 × 10 = 170 cm
तथा 25x = 25 × 10 = 250 cm
∴ अर्द्ध-परिमाप (s) = \(\frac{120+170+250}{2}\)
= \(\frac{540}{2}\) = 270 cm
अब हीरोन के त्रिभुज के क्षेत्रफल के सूत्र से

= 2 × 3 × 5 × 10 × 30 cm²
= 9000 cm²

प्रश्न 6.
एक समद्विबाहु त्रिभुज का परिमाप 30 cm है और उसकी बराबर भुजाएँ 12 cm लम्बाई की हैं। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार त्रिभुज का परिमाप = 30 cm
अर्थात् 12 cm + 12 cm + x = 30 cm
या 24 cm + x = 30 cm
या x = 30 cm - 24 cm
या x = 6 cm
i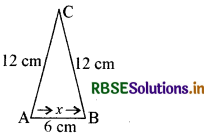
∴ त्रिभुज का अर्द्ध-परिमाप (s)
= \(\frac{12+12+6}{2}\)
= \(\frac{30}{2}\) = 15 cm
हीरोन के सूत्रानुसार ∆ का क्षेत्रफल