RBSE Solutions for Class 9 Maths Chapter 11 रचनाएँ Ex 11.2

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 11 रचनाएँ Ex 11.2 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 11 रचनाएँ Ex 11.2

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 7 cm, Z B = 75° और AB + AC = 13 cm हो।
हल:
प्रश्नानुसार दिया गया है कि आधार BC = 7 सेमी., ∠B = 75° तथा दो भुजाओं का योग अर्थात् AB + AC = 13 सेमी.। इनके आधार पर ∆ ABC की रचना करनी है।

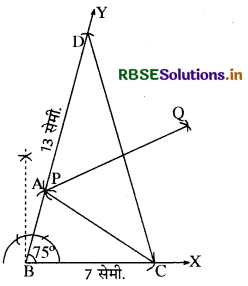
रचना के चरण

• सर्वप्रथम एक किरण BX खींची तथा इसमें से BC = 7 सेमी. ली।
• बिन्दु B पर परकार व पटरी की सहायता से ∠YBX = 75° की रचना की।
• अब B को केन्द्र मानकर परकार में 13 सेमी. (AB + AC = 13 सेमी.) लेकर एक चाप काटा जो BY को D बिन्दु पर मिलता है।
• बिन्दु C को D से मिला दिया।
• अब भुजा CD का लम्ब समद्विभाजक PQ खींचा जो BD भुजा के A बिन्दु पर मिलते हैं।
• A को C से मिला दिया। यही अभीष्ट त्रिभुज है।

हम जानते हैं कि A बिन्दु, CD भुजा के लम्ब समद्विभाजक पर स्थित है। अतः
AC = AD
∴ AB = BD - AD
⇒ AB = BD - AC
⇒ AB + AC = BD = 13 सेमी.

प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए, जिसमें BC = 8 cm, ∠B = 45° और AB - AC = 3.5 cm हो।
हल:
प्रश्नानुसार दिया गया है कि आधार BC = 8 सेमी., ∠B = 45° तथा दो भुजाओं में अन्तर अर्थात् AB - AC = 3.5 सेमी.। इनके आधार पर हमें ∆ ABC की रचना करनी है।

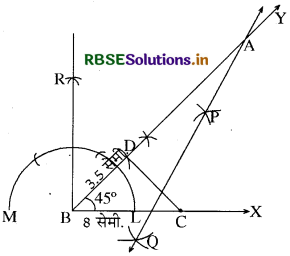
रचना के चरण:

• सबसे पहले एक किरण BX खींची तथा इसमें से BC रेखाखण्ड 8 सेमी. का खींचा।
• बिन्दु B पर 45° का कोण बनाया।
• अब रेखाखण्ड BY में से BD = 3.5 सेमी. [क्योंकि AB - AC = 3.5 सेमी.] काटा।
• बिन्दु C व D को मिला दिया।
• अब CD रेखा का लम्ब समद्विभाजक PQ खींचा जो BY रेखा के A बिन्दु पर मिलता है।
• A को C से मिलाया। इस प्रकार ∆ ABC बन गया।

बिन्दु A, CD के लम्ब समद्विभाजक पर स्थित है। अतः
AD = AC
अब BD = AB - AD
या BD = AB - AC
या BD = AB - AC = 3.5 सेमी.

प्रश्न 3.
एक त्रिभुज PQR की रचना कीजिए, जिसमें QR = 6 cm, ∠Q = 60° और PR - PQ = 2 cm हो। .
हल:
प्रश्नानुसार QR (आधार) = 6 सेमी. ∠Q = 60° (आधार का कोण) तथा PR - PQ = 2 सेमी.| अब इनके आधार पर ∆ PQR की रचना करनी है।
रचना के चरण:
(1) सर्वप्रथम एक किरण QX खींची तथा इसमें से रेखाखण्ड QR = 6 सेमी. का काटा।

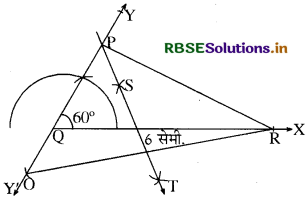
(2) Q बिन्दु पर परकार व पटरी की सहायता से 60° का कोण बनाती हुई किरण QY खींची। QY को इस प्रकार आगे बढ़ाया कि YQY' बन जाए।
(3) OY' में से रेखाखण्ड 00 = 2 सेमी. अर्थात् PR – PQ = 2 सेमी. का काटा।
(4) बिन्दु O को R से मिलाकर OR का लम्ब समद्विभाजक ST खींचा।
(5) P से R को मिला दिया। इस प्रकार अभीष्ट ∆ PQR बन गया।
∵ POR के लम्ब समद्विभाजक पर स्थित है अतः
PO = PR
या PQ + QO = PR
या QO = PR – PQ
या PR - PQ = 2 सेमी.

प्रश्न 4.
एक त्रिभुज XY∠ की रचना कीजिए, जिसमें ∠Y = 30°, ∠Z = 90° और XY + YZ + ∠X = 11 cm हो।
हल:
प्रश्नानुसार दिया गया है कि आधार का कोण ∠Y = 30° तथा एक कोण ∠Z = 90° है।
तीनों भुजाओं का योग या परिमाप = XY + YZ + ZX = 11 सेमी.। इनके आधार पर अब ∆ XYZ की रचना करनी है।

रचना के चरण:
(1) सर्वप्रथम एक PQ रेखाखण्ड 11 सेमी. का खींचा।।
(2) ∠Y = 30° होने के कारण P बिन्दु पर ∠KPQ = 30° की रचना की तथा ∠Z = 90° होने के कारण Q बिन्दु पर ∠LQP = 90° की रचना की।

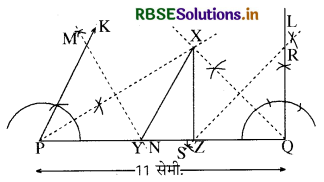
(3) ∠KPQ तथा ∠LQP को समद्विभाजित किया जो एक-दूसरे से X बिन्दु पर मिलते हैं।
(4) अब PX तथा QX भुजाओं का लम्ब समद्विभाजक क्रमश: MN तथा RS खींचा।
(5) ये लम्ब समद्विभाजक MN तथा RS भुजा या रेखाखण्ड PQ को Y तथा Z बिन्दुओं पर मिलते हैं।
(6) अब XY तथा XZ को मिला दिया। इस प्रकार ∆ XYZ की रचना हुई।

चित्रानुसार PX का लम्ब समद्विभाजक MN पर बिन्दु Y स्थित है।
अतः PY = XY
इसी प्रकार QZ = XZ
अतः XY + YZ + ZX = PY + YZ + QZ
= PQ = 11 सेमी.
पुनः ∠YXP = ∠XPY ।
[क्योंकि ∆ XPY में XY = PY]
अब ∠XYZ = ZY × P + ∠XPY
= 2 ∠XPY = ∠KPQ
या ∠XYZ = 30°
इसी प्रकार ∠XYZ = ∠LQP
या ∠XZY = 90°

प्रश्न 5.
एक समकोण त्रिभुज की रचना कीजिए, जिसका आधार 12 cm और कर्ण तथा अन्य भुजा का योग 18 cm है।
हल:
प्रश्नानुसार दिया गया है कि आधार QR = 12 सेमी., कर्ण व अन्य भुजा का योग अर्थात् PQ + PR = 18 सेमी. तथा ∠PQR = 90° है। अब इनसे हमें समकोण ∆ PQR की रचना करनी है।

रचना के चरण:
(1) सर्वप्रथम एक किरण OX खींची तथा इसमें से QR रेखाखण्ड 12 सेमी. का काटा। .
(2) ∠YQX = 90° बनाया तथा QY रेखा में से रेखाखण्ड QD = 18 सेमी. काटा।

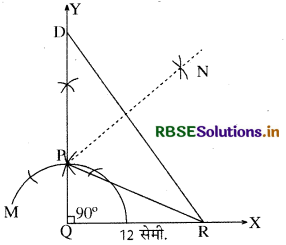
(3) बिन्दु D को R से मिला दिया।
(4) अब रेखाखण्ड DR का लम्ब समद्विभाजक खींचा जो QD को P बिन्दु पर काटता है।
(5) अब PR को मिलाया। इस प्रकार अभीष्ट ∆ PQR प्राप्त हुआ।
∵ बिन्दु P, DR के लम्ब समद्विभाजक पर स्थित है। अतः
PR = PD और तब
PQ = QD - PD
या PQ = QD - PR
या PQ + PR = QD = 18 सेमी.