RBSE Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 11 Constructions Ex 11.1

Question 1.
Construct an angle of 90° at the initial point of a given.ray and justify the construction.
Answer:

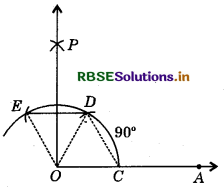
Steps of Construction :

1. Draw a ray OA.
2. With its initial point 0 as centre and any radius, draw an arc, cutting OA at C.
3. With centre C and same radius (as in step 2), draw an arc, cutting the previous arc at D.
4. With D as centre and the same radius, draw an arc cutting the previous arc at E.
5. With D and E as centres, and any convenient radius (more than \frac{1}{2} DE), draw two arcs intersecting each other at P.
6. Join OP.

Then, ∠AOP = 90°.
Justification : By construction, OC = CD = OD
∴ ∆OCD is an* equilateral triangle. So, ∠COD = 60°.
Again, OD = DE = EO
∴ ∆ODE is also an equilateral triangle. So, ∠DOE = 60°.
Since, OP bisects ∠DOE, so ∠POD = 30°.
Now, ∠AOP = ∠COD + ∠DOP = 60° + 30° = 90°.

Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Answer:
Steps of Construction :

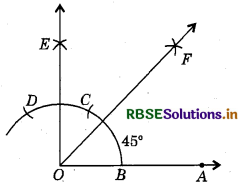
1. Draw a ray OA.
2. With O as centre and any suitable radius, draw an arc cutting OA at B.
3. With B as centre and same radius, cut the previous drawn arc at C and then with C as centre and same radius, draw arc to cut the previous arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius, draw another arc to cut the previous arc at E.
6. Join OE. Then, ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.

Then, ∠AOF = 45°.
Justification : By construction, ∠AOE = 90° and OF is the bisector of ∠AOE.
∴ ∠AOF = \frac{1}{2} ∠AOE = \frac{1}{2} × 90° = 45°.

Question 3.
Construct the angles of the following measurements :
(i) 30° (ii) 22\frac{1}{2}° (iii) 15°
Answer:
(i) Steps of Construction :

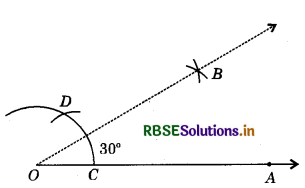
1. Draw a ray OA.
2. With its initial point O as centre and any radius, draw an arc, cutting OA at C.
3. With centre C and same radius (as in step 2), draw an arc, cutting the arc of step 2 inD.
4. With C and D as centres, and any convenient radius (more than \frac{1}{2}CD), draw two arcs intersecting each other at B.
5. Join OB.

Then, ∠AOB = 30°.

(ii) Steps of Construction :

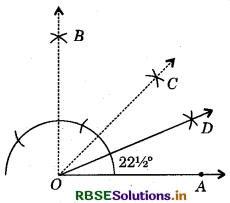
1. Draw an angle AOB = 90°.
2. Draw the bisector OC of ∠AOB, then ∠AOC = 45°.
3. Bisect ∠AOC, such that ∠AOD = ∠COD.

Thus, ∠AOD = 22\frac{1}{2}°.

(iii) Steps of Construction :

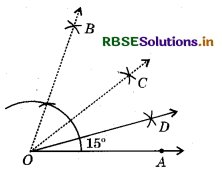
1. Construct an ∠AOB = 60°.
2. Bisect ∠AOB, so that ∠AOC = ∠BOC = 30°.
3. Bisect ∠AOC, so that ∠AOD = ∠COD.

Thus, ∠AOD = 15°.

Question 4.
Construct the following angles and verify by measuring them by a protractor:
(i) 75°
(ii) 105°
(iii) 135°
Answer:
(i) Steps of Construction :

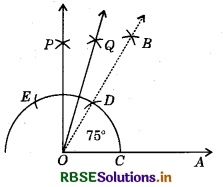
1. Draw a ray OA.
2. Construct ∠AOB = 60°.
3. Construct ∠AOP = 90°.
4. Bisect ∠BOP, so that

∠BOQ =\frac{1}{2} ∠BOP = \frac{1}{2} (∠AOP - ∠AOB)
= \frac{1}{2} (90°- 60°) = \frac{1}{2} × 30°= 15°
So, we obtain
∠AOQ = ∠AOP + ∠BOQ = 60° + 15° = 75°.
Verification : On measuring ∠AOQ, with the protractor, we find ∠AOQ = 75°

(ii) Steps of Construction :

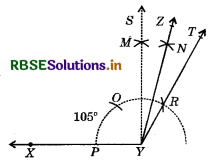
1. Draw a fine segment (or a ray) YX.
2. Construct ∠XYT = 120° and ∠XYS = 90°, so that
   ∠SYT = ∠XYT - ∠XYS
   = 120° - 90°
   = 30°
3. Bisect angle SYT, by drawing its bisector YZ.

Then, ∠XYZ is the required angle of 105°.

(iii) Steps of Construction :

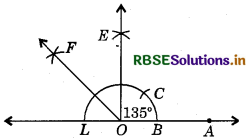
1. Draw ∠AOE = 90°.
Then, ∠LOE = 90°.

2. Draw the bisector OF of ∠LOE.
Then, ∠AOF = ∠AOE + ∠EOF
= 90° + 45° = 135°.

Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Answer:
Let us draw an equilateral triangle of side 4.6 cm (say).

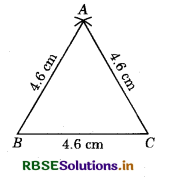
Steps of Construction :

1. Draw BC = 4.6 cm.
2. With B and G as centres and radii equal to BC = 4.6 cm, draw two arcs on the same side of BC, intersecting each other at A.
3. Join AB and AC.

Then, ABC is the required equilateral triangle.
Justification : Since by construction :
AB = BC - CA = 4.6 cm,
therefore AABC is an equilateral triangle.