RBSE Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.6

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.6 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.6

प्रश्न 1.
सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों की केन्द्रों की रेखा दोनों प्रतिच्छेद बिन्दुओं पर समान कोण अंतरित करती है।
हल:
माना कि दो वृत्त जिनके केन्द्र क्रमशः A और B हैं, परस्पर C और D पर प्रतिच्छेद करते हैं।

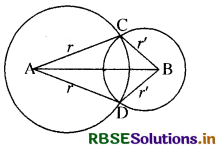
हमें सिद्ध करना है कि
∠ACB = ∠ADB
उपपत्ति- ∆ ABC और ∆ ABD में,
AC = AD (प्रत्येक = r )
BC = BD (प्रत्येक = r)
AB = AB (उभयनिष्ठ)
∴ ∆ ABC ≅ ∆ ABD
(सर्वांगसमता के नियम SSS के अनुसार)
⇒ ∠ACB = ∠ADB
(क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग)

प्रश्न 2.
एक वृत्त की 5 cm तथा 11 cm लम्बी दो जीवाएँ AB और CD समान्तर हैं और केन्द्र की विपरीत दिशा में स्थित हैं। यदि AB और CD के बीच की दूरी 6 cm हो, तो वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
मान लीजिए 0 वृत्त का केन्द्र है। OA और OC को मिलाइए।
क्योंकि वृत्त के केन्द्र से जीवा पर खींचा गया लम्ब जीवा को समद्विभाजित करता है।

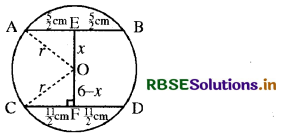
∴ AE = EB = \(\frac{1}{2}\)AB
= \(\frac{1}{2}\) × 5 cm
= \(\frac{5}{2}\) cm
और CF = FD = \(\frac{1}{2}\)CD
= \(\frac{1}{2}\) × 11 cm
= \(\frac{11}{2}\) cm
मान लीजिए OE = x,
∴ OF = 6 - x
मान लीजिए वृत्त की त्रिज्या है।
समकोण ∆ AEO में, पाइथागोरस प्रमेय के आधार पर
AO² = AE² + OE²

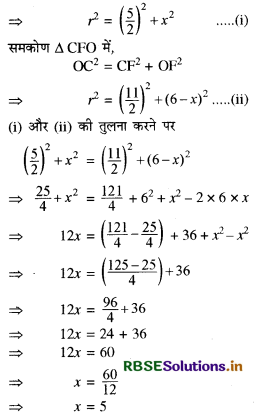
(i)

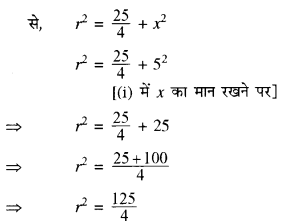
दोनों पक्षों का वर्गमूल लेने पर हमें प्राप्त होता है।
r = \(\sqrt{\frac{125}{4}}\)
⇒ r = \(\sqrt{\frac{5 \times 5 \times 5}{2 \times 2}}\)
⇒ r = \(\frac{5}{2} \sqrt{5}\)
अतः, वृत्त की त्रिज्या \(\frac{5}{2} \sqrt{5}\) cm है।

प्रश्न 3.
किसी वृत्त की दो समान्तर जीवाओं की लम्बाइयाँ 6 cm और 8 cm हैं। यदि छोटी जीवा केन्द्र से 4 cm की दूरी पर हो, तो दूसरी जीवा केन्द्र से कितनी दूर है ?
हल:
मान लीजिए AB = 6 cm और CD = 8 cm, O केन्द्र वाले वृत्त की जीवाएँ हैं।
OA और OC को मिलाइए।

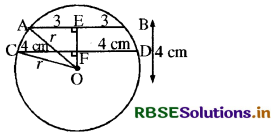
क्योंकि वृत्त के केन्द्र से जीवा पर खींचा गया लम्ब जीवा को समद्विभाजित करता है।
∴ AE = EB = \(\frac{1}{2}\)AB
= \(\frac{1}{2}\) × 6
= 3 cm
और CF = FD = \(\frac{1}{2}\)CD
= \(\frac{1}{2}\) × 8
= 4 cm
जीवा AB की केन्द्र 0 से लंबात्मक दूरी OE है।
∴ OE = 4 cm
अब समकोण ∆ AOE में,
OA² = AE² + OE²
[पाइथागोरस का परिणाम प्रयोग करने पर]
⇒ r² = 3² + 4²
⇒ r² = 9 + 16
⇒ r² = 25
⇒ r² = √25
⇒ ∴ r = 5 cm
जीवा CD की केन्द्र 0 से लंबात्मक दूरी OF है। समकोण ∆ OFC में,
OC² = CF² + OF²
[पाइथागोरस का परिणाम प्रयोग करने पर
⇒ r² = 4² + OF²
⇒ 5² = 4² + OF²
या OF² = 25 - 16
⇒ OF² = 9
⇒ OF = √9
⇒ OF = 3 cm
अतः, दूसरी जीवा की केन्द्र से दूरी 3 cm है।

प्रश्न 4.
मान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएँ AD और CE काटती हैं। सिद्ध कीजिए कि ∠ABC जीवाओं AC तथा DE द्वारा केन्द्र पर अंतरित कोणों के अन्तर का आधा है।
हल:
∠ABC का शीर्ष B एक वृत्त (जिसका केन्द्र 0 है) के बाहर स्थित है।

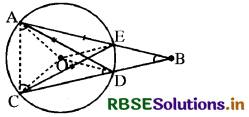
भुजा AB, जीवा CE को बिन्दु E पर प्रतिच्छेद करती है और BC जीवा AD को बिन्दु D पर प्रतिच्छेद करती है।
हमें सिद्ध करना है कि
∠ABC = \(\frac{1}{2}\)[∠AOC - ∠DOE)
OA, OC, OE और OD को मिलाइए।
अब, ∠AOC = 2 ∠AEC
[चाप द्वारा केन्द्र पर अंतरित कोण वृत्त के शेष भाग के किसी बिन्दु पर अंतरित कोण का दुगुना होता है]
अतः \(\frac{1}{2}\)∠AOC = ∠AEC ....... (i)
इसी प्रकार,
\(\frac{1}{2}\)∠DOE = ∠DCE ....... (ii)
(i) में से (ii) को घटाने पर
\(\frac{1}{2}\)[∠ AOC - ∠DOE] = ∠ AEC - ∠DCE ...... (iii)
अब, ∠AEC = ∠ADC .....(iv) (एक ही वृत्तखण्ड के कोण)
साथ ही, ∠DCE = ∠DAE ..... (v) (एक ही वृत्तखण्ड के कोण)

(iv) और (v) को (iii) में प्रयोग करने पर हमें प्राप्त होता है,
\(\frac{1}{2}\)[∠ AOC - ∠ DOE] = ∠ADC - ∠ DAE ...... (vi)
∆ ADB में,
∠ADC = ∠ DAE + ∠ABD .....(vii)
(त्रिभुज का बाह्य कोण अंत:अभिमुख कोणों के योग के बराबर होता है)
(vii) को (vi) में प्रयोग करने पर हमें प्राप्त होता है-
\(\frac{1}{2}\)[∠AOC - ∠ DOE] = ∠ DAE + ∠ ABD - ∠ DAE
⇒ \(\frac{1}{2}\)[∠AOC - ∠ DOE] = ∠ABD
या \(\frac{1}{2}\)[∠AOC - ∠DOE] = ∠ ABC

प्रश्न 5.
सिद्ध कीजिए कि किसी समचतुर्भुज की किसी भुजा को व्यास मानकर खींचा गया वृत्त उसके विकर्णों के प्रतिच्छेद बिन्दु से होकर जाता है।
हल:
मान लीजिए कि ABCD एक समचतुर्भुज है जिसमें विकर्ण AC और BD परस्पर बिन्दु 0 पर प्रतिच्छेद करते हैं।

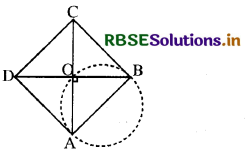
हम जानते हैं कि समचतुर्भुज के विकर्ण एकदूसरे के लम्ब समद्विभाजक होते हैं।
∴ ∠AOB = 90°
यदि हम AB को व्यास मानकर वृत्त खींचें तो यह निश्चित रूप से ही बिन्दु ) (विकर्णों का प्रतिच्छेद बिन्दु) में से होकर जाएगा क्योंकि तब ∠AOB = 90° इसके अर्धवृत्त में बना कोण होगा। (इति सिद्धम्)

प्रश्न 6.
ABCD एक समान्तर चतुर्भुज है। A, B और C से जाने वाला वृत्त CD (यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
हल:
आकृति (a) में,
ABCD एक समान्तर चतुर्भुज है।
⇒∠1 = ∠3 ........... (i)
(समान्तर चतुर्भुज के सम्मुख कोण)

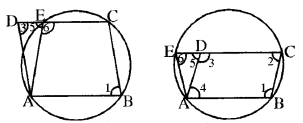
ABCE एक चक्रीय चतुर्भुज है।
∠1 + ∠6 = 180°
∠5 + ∠6 = 180°
(रैखिक युग्म) .....(iii)
(ii) और (iii) से
∠1 = ∠5 ...... (iv)
अब, (i) और (iv) से
∠3 = ∠5
अब, ∆ AED में,
∠3 = ∠5
⇒ AE = AD
(∵ त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ) आकृति (b) में,
ABCD एक समान्तर चतुर्भुज है।
⇒ ∠1 = ∠3
(समान्तर चतुर्भुज के सम्मुख कोण)
∠2 = ∠4
साथ ही AB || CD और BC इनको मिलती है।
∠1 + ∠2 = 180° ......(i)
और AD || BC और EC इनको मिलती है।
∠5 = ∠2 (संगत कोण) .......(ii)
ABCE एक चक्रीय चतुर्भुज है
∴ ∠1 + ∠6 = 180° .......(iii)
(i) और (iii) से हमें प्राप्त होता है
∠1 + ∠2 = ∠1 + ∠6
⇒ ∠2 = ∠6
परन्तु (ii) से,
∠2 = ∠5
⇒ ∠5 = ∠6
अब, ∆ AED में,
∠5 = ∠6
⇒ AE = AD
अतः, दोनों स्थितियों में,
AE = AD (इति सिद्धम् )

प्रश्न 7.
AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध कीजिए
(i) AC और BD व्यास हैं,
(ii) ABCD एक आयत है।
हल:
(i) मान लीजिए वृत्त की जीवाएँ AC और BD परस्पर 0 पर समद्विभाजित करती हैं।
तो OA = OC और OB = OD

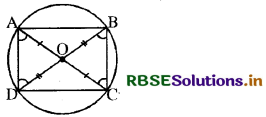
हमें सिद्ध करना है कि (i) AC और BD व्यास हैं, दूसरे शब्दों में, 0 वृत्त का केन्द्र है।
यहाँ पर OA, OB, OC और OD एक ऐसे वृत्त की त्रिज्यायें हैं जिसका केन्द्र 0 है। तब
AC = OA + OC
= त्रिज्या + त्रिज्या
= 2 × त्रिज्या
= व्यास
अत: AC वृत्त का व्यास है।
∵ BD भी 0 बिन्दु से गुजरती है।
∴ BD भी वृत्त का व्यास होगा।
(ii) AC वृत्त का व्यास है।
∴ AC द्वारा अर्द्धवृत्त में बने कोण
∠ABC = ∠ADC = 90° होंगे।
इसी प्रकार BD व्यास द्वारा अर्द्धवृत्त में बने कोण
∠ BAD = ∠BCD = 90° हैं।
अत: ABCD एक ऐसा चतुर्भुज है जिसका प्रत्येक कोण 90° तथा विकर्ण एक-दूसरे को समद्विभाजित करते
⇒ ABCD एक आयत है। (इति सिद्धम् )

प्रश्न 8.
एक त्रिभुज ABC के कोणों A, B और C के समद्विभाजक इसके परिवृत्त को क्रमश: D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण 90° - \(\frac{1}{2}\)A, 90° - \(\frac{1}{2}\)B तथा 90° - \(\frac{1}{2}\)c हैं।
हल:
दिया है- ∆ ABC के कोणों A, B और C के समद्विभाजक AD, BE व CF त्रिभुज के परिवृत्त को क्रमशः बिन्दुओं D, E व F पर काटते हैं। बिन्दुओं D, E व F से त्रिभुज DEF बनाया गया है।
सिद्ध करना है:
∆ DEF में

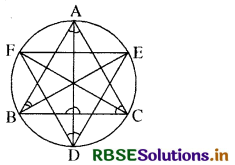
∠D = 90° - \(\frac{1}{2}\)A.
E = 90° - \(\frac{1}{2}\)B
और F = 90° - \(\frac{C}{2}\)
उपपत्ति- ∵ ∠ADE और ∠ABE एक ही चाप AE द्वारा बने हैं।
∴∠ADE = ∠ABE
∴ \(\frac{1}{2}\)∠D = \(\frac{1}{2}\)∠C ....(i)
समीकरण इसी प्रकार ∠ADF और ∠ ACF एक ही चाप AF द्वारा बने हैं।
∴∠ADF = ∠ ACF
∴ \(\frac{1}{2}\)∠D = \(\frac{1}{2}\)∠C .....(ii)
समीकरण (i) व (ii) को जोड़ने पर
∠D = \(\frac{1}{2}\) (∠B + ∠C)
∵∠B + 2 C = 180° - ∠A
∠D = \(\frac{1}{2}\)(180° - ∠A)
= 90° - \(\frac{1}{2}\)∠A
या ∠D = 90° - \(\frac{1}{2}\)A
इसी प्रकार सिद्ध कर सकते हैं कि
∠E = 90° - \(\frac{1}{2}\)B तथा ∠F = 90° - \(\frac{1}{2}\)C
अत: ∆ DEF के कोण क्रमश: 90° - \(\frac{1}{2}\)A, 90° - \(\frac{1}{2}\)B, 90° - \(\frac{1}{2}\)C हैं।

प्रश्न 9.
दो सर्वांगसम वृत्त परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखण्ड FAQ इस प्रकार खींचा गया है कि P और Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।
हल:
दिया है-दो सर्वांगसम वृत्त बिन्दुओं A और B पर प्रतिच्छेद करते हैं।
A से खींची गई रेखा वृत्तों को P और Q पर मिलती है।

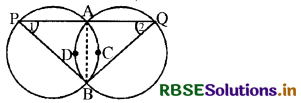
सिद्ध करना है-BP = BQ
रचना-A और B को मिलाइए।
उपपत्ति-AB उभयनिष्ठ जीवा है और वृत्त बराबर हैं।
∴ उभयनिष्ठ जीवा के संगत चाप बराबर होते हैं। अर्थात्

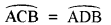
क्योंकि दो सर्वांगसम वृत्तों के सर्वांगसम चाप वृत्त के शेष भाग पर बराबर कोण बनाते हैं। इसलिए,
∠1 = ∠2
∆ PBQ में ∠1 = ∠2(सिद्ध कर चुके हैं)
∴ त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं। इसलिए
BP = BQ.

प्रश्न 10.
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लम्ब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ∆ ABC के परिवृत्त पर प्रतिच्छेद करेंगे।
हल:
दिया है-ABC एक त्रिभुज है और इसके शीर्षों में से वृत्त गुजरता है।
मान लीजिए कि कोण A का समद्विभाजक तथा सम्मुख भुजा BC का लम्ब समद्विभाजक (कह लीजिए) बिन्दु P पर प्रतिच्छेद करते हैं।
सिद्ध करना है-त्रिभुज ABC का परिवृत्त भी बिन्दु P में से होकर जाएगा।

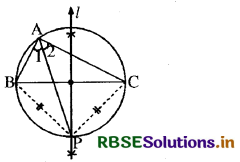
उपपत्ति: हम जानते हैं कि किसी भुजा के लंब समद्विभाजक पर कोई भी बिन्दु इस संगत भुजा के अंत:बिन्दुओं से समदूरस्थ होता है।
∴ BP = PC ..... (i)
साथ ही प्राप्त है- ∠1 = ∠2 .....(ii)
[क्योंकि, AP, ∠A का समद्विभाजक है । (दिया है)]
(i) और (ii) से हमें ज्ञात होता है कि बराबर रेखाखण्ड वृत्त के एक ही खण्ड (अर्थात् ∆ ABC के परिवृत्त के बिन्दु A पर) में बराबर कोण बनाते हैं।
इसलिए BP और PC; ∆ ABC के परिवृत्त की जीवाओं के रूप में हैं और उनकी संगत चापें; \(\widehat{\mathrm{BP}}\) और \(\widehat{\mathrm{PC}}\) परिवत्त के ही भाग हैं।
अतः बिन्दु P परिवृत्त पर ही है।
दूसरे शब्दों में, बिन्दु A, B, P और C एकवृत्तीय हैं।