RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 10 Circles Ex 10.6

Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Answer:
Given : Two circles with centres A and B, which intersect each other at C and D.
To prove : ∠ACB = ∠ADB.

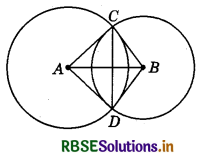
Construction : Join AC, AD, BD and BC.
Proof : In As ACB and ADB, we have :
AC = AD (Radii of the same circle)
BC = BD (Radii of the same circle)
AB = AB (Common)
By SSS criterion of congruence,
∆ACB = ∆ADB
So, ∠ACB = ∠ADB - (CPCT)
Hence proved.

Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Answer:
Let O be the centre of the given circle and let its radius be r cm. Draw OP ⊥ AB and OQ ⊥ CD. Since, OP ⊥ AB, OQ ⊥ CD and AB ∥ CD, therefore points P, O and Q are collinear. Now, PQ = 6 cm.
Let OP = x. Then, OQ = (6 - x) cm.
Join OA and OC. Then, OA = OC = r.

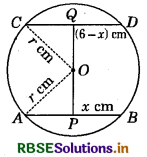
Since, the perpendicular from the centre to a chord of the circle bisects the chord, therefore AP = PB = 2.5 cm and CQ = QD = 5.5 cm.
In right As OAP and OCQ, we have :
OA² = OP² + AP² and OC² = OQ² + CQ²
⇒ r² = x² + (2.5)² .............(1)
and r² = (6 - x)² + (5.5)² ............(2)
So, x² + (2.5)² = (6 - x)² + (5.5)²
or x² + 6.25 = 36 - 12x + x² + 30.25
⇒ 12x = 60 ⇒ x = 5

Putting x = 5 in (1), we get :
r² = 5² + (2.5)² = 25 + 6.25 = 31.25 .
So, r = \(\sqrt{31.25}\) = 5.6 (approx.)
Hence, the radius of the circle is 5.6 cm (approx.).

Or

Calculations (not using decimal)

Hence, the radius of circle is \(\frac{5 \sqrt{5}}{2}\) cm.

Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre?
Answer:
Let AB and CD be two parallel chords of a circle with centre O such that AB = 6 cm and CD = 8 cm.

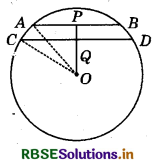
Let the radius of the circle be r cm.
Draw OP ⊥ AB and OQ ⊥ CD. Since, AB ∥ CD, OP ⊥ AB and OQ ⊥ CD, therefore, points O, Q and P are collinear.
Clearly OP = 4 cm and P and Q axe mid-points of AB and CD respectively.
∴ AP = PB = \(\frac{1}{2}\) AB = 3 cm
and, CQ = QD = \(\frac{1}{2}\)CD = 4 cm

In rt. ∠d triangle OAP, we have :
OA² = OP² + AP²
So, r² = 4² + 3² = 16 + 9 = 25
r = 5

In rt. ∠d triangle OCQ, we have :
OC² = OQ² + CQ²
So, r2 = OQ² + 4²
25 = OQ² +16
OQ² = 9 ⇒ OQ = 3
Hence, the distance of the chord CD from the centre is 3 cm.
Note : If chord CD is taken on the other side of the centre O, even then its distance from O will be 3 cm.

Question 4.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Answer:
We know that an exterior angle of a triangle is equal to the sum of the interior opposite angles.

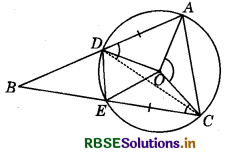
In ∆BDC, we have :
∠ADC = ∠DBC + ∠DCB .....(1)
Since, angle at the centre is twice the angle at a point on the remaining part of circle, therefore
∠ADC = \(\frac{1}{2}\)∠AOC
and
∠DCB = \(\frac{1}{2}\)∠DOE
From (1) and (2), we have :
∴ \(\frac{1}{2}\)∠AOC = ∠ABC + \(\frac{1}{2}\)∠DOE
∠ABC = \(\frac{1}{2}\)(∠AOC - ∠DOE)
Hence, ∠ABC is equal to half the difference of angles subtended by the chords AC and DE at the centre.
Hence proved.

Question 5.
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals
Answer:
Given : ABCD is a rhombus. AC and BD are its two diagonals which bisect each other at right angles.

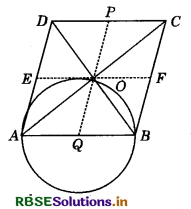
To prove : A circle drawn on AB as diameter will pass through O.
Construction : Through O, draw PQ ∥ AD and EF ∥ AB.
Proof : ∴ AB = DC
⇒ \(\frac{1}{2}\)AB = \DC
So, AQ = DP (∵ Q and P are mid-points of AB and CD.)
Similarly, AE = OQ
So, AQ = OQ = QB
A circle drawn with Q as centre and radius AQ passes through A, O and B.
The circle thus obtained is the required circle.

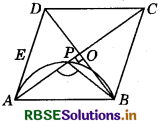
Aliter : Let us assume that the circle with AB as diameter, does not pass through O and let it intersect at some other point P (see figure).
Then ∠APB = 90°
Also, ∠AOB = 90
∴ ∠APB must be equal to ∠AOB.
This is not possible. It will be possible only when O and P coincide. Hence proved.

Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Answer:
In order to prove that AE = AD, i.e. ∆AED is an isosceles triangle, it is sufficient to prove that
∠AED = ∠ADE.

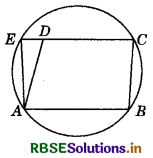
Since, ABCE is a cyclic quadrilateral, therefore
∠AED + ∠ABC = 180° ..................(1)
Now, CDE is a straight line.
∴ ∠ADE + ∠ADC = 180°
So, ∠ADE + ∠ABC = 180° ............. (2)
(∵ ∠ADC and ∠ABC are opposite angles of a ∥gm, i.e. ∠ADC = ∠ABC)
From (1) and (2), we get:
∠AED + ∠ABC = ∠ADE + ∠ABC
⇒ ∠AED = ∠ADE
∴ In ∆AED, we have : ∠AED = ∠ADE
So, AD = AE.
Hence proved.

Question 7.
AC and BD are chords of a circle which bisect each other. Prove that :
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
Answer:
(i) Let AC and BD be Let they bisect each other at O.

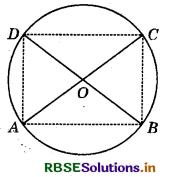
Join AB, BC, CD and DA.
In ∆s AOB and COD, we have :
OA = OC (∵ O is the mid-point of AC.)
∠AOB = ∠COD (Vert. opp. ∠s)
and OB = OD (∵ O is the mid-point of BD.)

By SAS criterion of congruence,
∆AOB ≅ ∆COD
So, \(\widehat{A B}=\widehat{C D}\)
⇒ AB = CD

Similarly, from ∆s AOD and COB, we have:
\(\widehat{A B}=\widehat{C D}\)
From (1) and (2)
\(\widehat{A B}+\widehat{A D}=\widehat{C D}+\widehat{C B}\)

∴ BD divides the circle into two equal parts.
So, BD is a diameter.
Similarly, AC is a diameter.

(ii) Now, AC and BD bisect each other.
So, ABCD is a parallelogram. (Given)
Also, AC = BD (Diameters are equal.)
So, ABCD is a rectangle. Hence proved.

Question 8.
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEE are 90° - \(\frac{1}{2}\)A, 90° - \(\frac{1}{2}\)B and 90° - \(\frac{1}{2}\)C.
Answer:

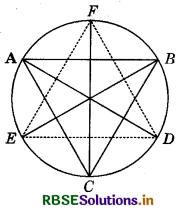
We have :
∠D = ∠EDF = ∠EDA + ∠ADF
= ∠EBA + ∠FCA (∵ ∠EDA and ∠EBA are the angles in the same segment of the circle.)
∠EDA = ∠EBA.

Similarly, ∠ADF and ∠FCA are the angles in the same segment and hence, ∠ADF = ∠FCA.
= \(\frac{1}{2}\)∠B + \(\frac{1}{2}\)∠C
(∵ BE is the bisector of ∠B and CF is the bisector of ∠C.)

Thus, the angles of the ∆DEF are 90° - \(\frac{1}{2}\)A, 90° - \(\frac{1}{2}\)B and 90° -  \(\frac{1}{2}\)C.
Hence proved.

Question 9.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Answer:

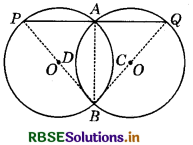
Let O and O' be the centres of two congruent circles.
Since, AB is a common chord of these circles, therefore
arc ACB = arc ADB
So, ∠BPA = ∠BQA
BP = BQ (Sides opposite to equal angles of triangle BPQ)
Hence proved.

Question 10.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
Answer:
Let ABC be a triangle such that O is the centre of its circumdrcle.

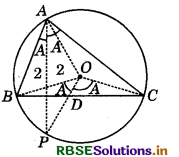
Clearly, arc BC makes angle A at point A on the circle.
∴ ∠BOC = 2∠A
But OB = OC (Radii of the same circle)
∴ ∠BOD = ∠COD = ∠A
Let the bisector of angle A and perpendicular bisector of BC intersect at point P.
Since, any three non-colinear points are always concyclic, therefore A, C and P are concyclic. Arc CP makes angle \frac{A}{2} at point A and angle A at O. Therefore, O is the centre of the circle passing through A, C and P, which is also the centre of the drcumdrcle of AABC. That is, drde passing through A, C and P is the circumdrcle of ∆ABC.

Similarly, the drde passing through A, B and P is the circumdrcle of ∆ABC. Hence, P lies on the drcumdrcle of ∆ABC. Hence proved.

Aliter :
1. Let bisector of ∠A meet the drcumdrcle of ∆ABC at P. Join BP and CP (see figure).
∠PBC = ∠PAC (Angles in the same segment)
and ∠PCB = ∠BAP (Angles in the same segment)
But ∠BAP = ∠CAP (∵ AP is bisector of ∠A)
∴ ∠PBC= ∠PCB
So, PB = PC (Sides opposite the equal angles of ∆PBC)
So, P must lie on the perpendicular bisector of BC.
i. e. bisector of ∠A and perpendicular bisector of BC meet at the drcumdrcle of ∆ABC.

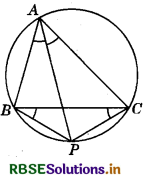
2. Let P is a point on the perpendicular bisector of BC which lies on circumdrcle of AABC.
Join AP (see figure).
As P lies on perpendicular bisector of BC, therefore
BP = CP
So, ∠PBC = ∠PCB ..................(1) (Angles opposite the equal sides)
But ∠PBC = ∠PAC and ∠PCB = ∠BAP (Angles in the same segment)
So, from (1), ∠BAP = ∠CAP.
That is, AP is the bisector of A. Thus, bisector of ∠A and perpendicular bisector of BC meet at P which lies on circumcirde of ∆ABC.