RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.5

Question 2.
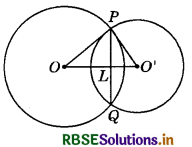
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the nugor arc.
Answer:
Let PQ be chord, which is equal to the radius. Join OP and OQ, where O is the centre of the circle.
It is given that PQ = OP = OQ (∵ Chord = Radius)

∴ ∆OPQ is equilateral.
So, ∠POQ = 60°
Since, arc PAQ makes reflex ∠POQ = 360° - 60° = 300° at the centre of the circle and ∠PBQ at a point in the minor arc of the circle, therefore

∠PBQ = \(\frac{1}{2}\) (reflex ∠POQ) = \(\frac{1}{2}\) × 300° = 150°
Similarly, ∠PAQ = \(\frac{1}{2}\)(∠POQ) = \(\frac{1}{2}\)(60°) = 30°
Hence, angle subtended by the chord at a point on the minor arc is 150° and on the major chord is 30°.

Question 3.
In the figure, ∠PQR = 100°, where P, Q and It are points on a circle with centre O. Find ∠OPR.

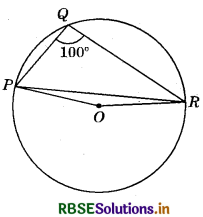
Answer:
Since the angle subtended by an arc of a circle at its centre is twice the angle subtended by the same arc at a point on the remaining part of the circle, therefore,
Reflex ∠POR = 2 ∠PQR
So, Reflex ∠POR = 2 × 100° = 200°
Further, ∠POR = 360° - 200° = 160°
In ∆OPR, OP = OR (Radii of the same circle)
∠OPR = ∠ORP (Angles opp. to equal sides are equal.)
∠POR = 160° (Proved above)
∴ ∠OPR = ∠ORP = \(\frac{1}{2}\)(180° - 160°) = \(\frac{1}{2}\) × 20° = 10°
Hence, ∠OPR = 10°

Question 4.
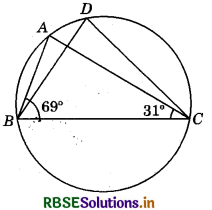
In the figure, ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.

Answer:
In ∆ABC,
∠BAC + ∠ABC + ∠BCA = 180°
∠BAC + 69° + 31° = 180° or ∠BAC = 180° - (69° + 31°)
= 180° - 100° = 80°
Since angles in the same segment are equal, therefore ∠BDC = ∠BAC = 80°.

Question 5.
In the figure, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.

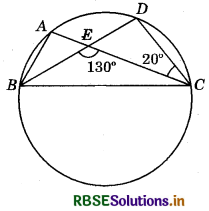
Answer:
∠CED + ∠CEB = 180° (Linear pair)
∠CED + 130° = 180°
or ∠CED = 180° - 130° = 50°

In ∆ECD,
∠EDC + ∠CED + ∠ECD = 180°
So, ∠EDC + 50° + 20° = 180°
or ∠EDC = 180° - 50° - 20° = 110°
∴ ∠BDC = ∠EDC =110°
Since.angles in the same segment are equal, therefore
∠BAC = ∠BDC = 110°.

Question 6.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70° and ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
Answer:

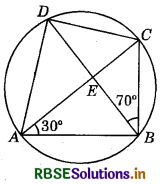
∠BDC = ∠BAC (Angles in the same segment)
∠BDC = 300 [∵ ∠BAC = 30° (Given)]

In ABCD, we have:
∠BDC + ∠DBC + ∠BCD = 180° (Sum of ∠s of a ∆)
So, 30° + 70° + ∠BCD = 180°
(∠DBC = 70°, ∠BDC = 30°)
∠BCD = 180° - 30° - 70° = 80°

If AB = BC, then ∠BCA = ∠BAC = 30° (Angles opp. to equal sides in a i are equal)
Now, ∠ECD = ∠BCD - ∠BCA = 80° - 30° = 50°
(∠BCD = 800 (found above) and ∠BCA = 30°)
Hence, ∠BC’D = 80° and ∠ECD = 50°.

Question 7.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Answer:
Given : Diagonals AC and BD of a cyclic quadrilateral are diameters of the circle through the vertices A, B, C and D of the quad. ABCD.
To prove : Quadrilateral ABCD is a rectangle.

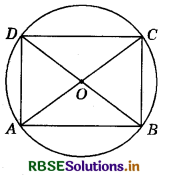
Proof: Since, all the radii of the same circle are equal.
OA = OB = OC = OD
or OA = OC = \(\frac{1}{2}\)AC
and OB = OD = \(\frac{1}{2}\)BD
AC = BD
The diagonals of the quadrilateral ABCD are equal and bisect each other.
So, quadrilateral ABCD is a rectangle.

Question 8.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer:
Given : Non-parallel sides AD and BC of a trapezium ABCD are equal.
To prove : ABCD is a cyclic trapezium.

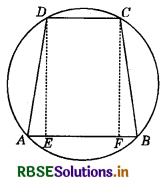
Construction : Draw DE ⊥ AB and CF ⊥ AB.
Proof: In order to prove that ABCD is a cyclic trapezium,
it is sufficient to prove that ∠B + ∠D = 180°.
in ∠s DEA and CFB, we have:
AD = BC (Given)
∠DEA = ∠CFB (Each = 90°)
and DE = CF (Distance between two lines is always equal.)

∴ By RHS criterion of congruence, we have:
∆DEA ≅ ∆CFB
So, , ∠A = ∠B and ∠ADE = ∠BCF (CPCT)
Now, ∆ADE = ∠BCF
So, 90° + ∠ADE = 90° + ∠BCF
∠EDC + ∠ADE = ∠FCD + ∠BCF ( ∠EDC = 90° and ∠FCD = 90°)

So, ∠ADC = ∠BCD
i.e. ∠D = ∠C
Thus, ∠A = ∠B and ∠C = ∠B .............(1)
But ∠A + ∠B + ∠C +∠D = 360° (∵ Sum of the angles of a quad, is 360°.)
∴ 2 ∠B + 2 ∠D = 360°
or ∠B + ∠D = 180°
Hence, ABCD is a cyclic trapezium.

Question 9.
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see figure). Prove that ∠ACP = ∠QCD.
Answer:

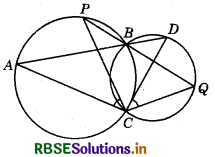
Since, angles in the same segment are equal, therefore
∠ACP = ∠ABP ...........(1)
and ∠QCD = ∠QBD ............(2)
Also, ∠ABP = ∠QBD (Vertically opp. angles) ..............(3)
From (1), (2) and (3), we have :
∠ACP = ∠QCD.
Hence proved.

Question 10.
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Answer:
Given : Two circles are drawn with sides AB and AC of ∆ABC as diameters. The circles intersect each other at D.
To prove : D lies on BC.
Construction : Join A and D.

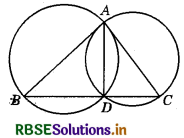
Proof : Now, AB and AC are the diameters of the two
∴ ∠ADB = 90° ....(1) (Angles in a semicircle)
and ∠ADC = 90° ....(2) (Angles in a semicircle)
Adding (1) and (2), we get :
∠ADB + ∠ADC = 90° + 90° = 180°
So, BDC is a straight line.
Hence, D lies on BC.
Hence Proved.

Question 11.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Answer:
As ABC and ADC are right ∠d with common hypotenuse AC. Draw a circle with AC as diameter passing through B and D. Join BD (see the figure).

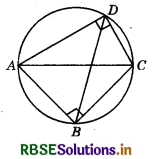
Clearly, ∠CAD = ∠CBD (∵ Angles in the same segment are equal.)
Hence Proved.

Question 12.
Prove that a cyclic parallelogram is a rectangle.
Answer:
Given : ABCD is a parallelogram inscribed in circle.
To prove : ABCD is a rectangle.

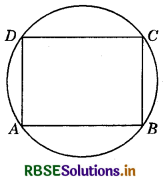
Proof: Since, ABCD is a cyclic quadrilateral, therefore
∠A + ∠C = 180° ............(1)
But ∠A = ∠C ........(2)
From (1) and (2), we have:
∠A = ∠C = 90°
Similarly, ∠B = ∠D = 90°
∴ Each angle of ABCD is of 90°.
Hence, ABCD is a rectangle.
Hence Proved.