RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.4
Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.4 Textbook Exercise Questions and Answers.
Rajasthan Board RBSE Solutions for Class 9 Maths in Hindi Medium & English Medium are part of RBSE Solutions for Class 9. Students can also read RBSE Class 9 Maths Important Questions for exam preparation. Students can also go through RBSE Class 9 Maths Notes to understand and remember the concepts easily. Practicing the class 9 math chapter 13 hindi medium textbook questions will help students analyse their level of preparation.
RBSE Class 9 Maths Solutions Chapter 10 Circles Ex 10.4
Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Answer:
Let O and O' be the centres of the circles of radii 5 cm and 3 cm respectively and let PQ be their common chord. We have OP = 5 cm, O'P = 3 cm and OO’ = 4 cm.
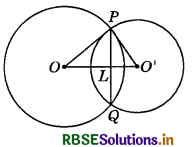
Since OP2 = PO'2 + O'O2, therefore (∵ 52 = 32 + 42)
OO'P is a right-angled triangle, right-angled at O'.
Now, Area of ∆OO'P = \(\frac{1}{2}\) × O'P × OO'
= \(\frac{1}{2}\) × 3 × 4
= 6 sq. units ................ (1)
Also, area of ∆OO'P = \(\frac{1}{2}\) × OO' × PL
= \(\frac{1}{2}\) × 4 × PL = 2 PL ........(2)
From (1) and (2), we have :
2 × PL = 6 ⇒ PL = 3 We know that when two circles intersect at two points, then their centre lie on the perpendicular bisector of the common chord, i.e. OO' is the perpendicular bisector of PQ.
PQ = 2 × PL = (2 × 3) cm = 6 cm.

Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Answer:
Given : AB and CD are chords of a circle with centre O. AB and CD intersect at P and AB = CD.
To prove : (i) AP = PD, (ii) PB = CP.
Construction : Draw OM ⊥ AB and ON ⊥ CD.
Join OP.
Proof : AM = MB = \(\frac{1}{2}\)AB
CN = ND = \(\frac{1}{2}\)CD (Perpendicular from centre bisects the chord)
AM = ND and MB = CN [∵ AB = CD (Given)] ............. (1)
In ∆s OMP and ONP, we have :
OM = ON (Equal chords of a circle are equidistant from the centre.)
∠OMP = ∠ONP (∵ Each = 90°)
OP = OP (Common)
By RHS criterion of congruence,
∆OMP ≅ ∆ONP
So, MP = PN (CPCT) ............... (2)
Adding (1) and (2), we have :
AM + MP = ND + PN
or
AP = PD
Subtracting (2) from (1), we have :
MP - MP = CN - PN
or
PB = CP
Hence, (i) AP = PD and (ii) PB = CP.
Hence proved.
Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer:
Given : AB and CD are chords of a circle with centre O. AB and CD intersect at P and AB = CD.
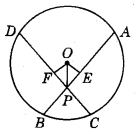
To prove : ∠OPE = ∠OPF.
Construction : Draw OE ⊥ AB and OF ⊥ CD. Join OP.
Proof : In ∆s OEP and OFP, we have :
∠OEP = ∠OFP (∵ Each = 90°)
OP = OP (Common)
OE = OF (Equal chords of a circle are equidistant from the centre.)
∴ By RHS criterion of congruence, we have :
∆OEP = ∆OFP
So, ∠OPE = ∠OPF
Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see figure).
Answer:
Let OM be the perpendicular from O on line l. We know that the perpendicular from the centre of a circle to a chord, bisects the chord.
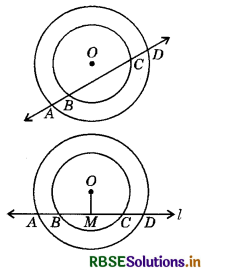
Now, BC is a chord of the smaller circle and OM ⊥ BC.
∴ BM = CM (1)
Again, AD is a chord of the larger circle and OM ⊥ AD.
∴ AM = DM .....(2)
Subtracting (1) from (2), we get :
AM - BM = DM - CM ⇒ AB = CD.

Question 5.
Three girls Reshma, Salma and Mandip are playing a game hy standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Answer:
Let the three girls Reshma, Salma and Mandip are standing on the circle of radius 5 m at points B, A and C respectively.
Now, in ∆s ABO and ACO,
AB = AC (Each = 6 m)
BO = CO (Each = 5 m)
AO = AO (Common)
∆ABO = ∆ACO (SSS congruence rule)
∠BAO = ∠CAO (CPCT)
So, the bisector of ∠BAC passes through the centre O, i.e.
AO is the bisector of ∠BAC.
Now, in ∆s ABM and ACM, we have :
AB = AC
AM =AM
and ∠BAM = ∠CAM
∴ ∆ABM = ∆ACM
So, BM = CM
and ∠BMA = ∠CMA = 90°
Now, M is the mid-point of BC and OM ⊥ BC.
Draw OL ⊥ AB.
Area of EOAB = \(\frac{1}{2}\) × OA × BM
= \(\frac{1}{2}\) × 5 × BMm2
Also, area of ∆OAB = \(\frac{1}{2}\) × AB × OL
OL2 = OB2 - BL2
= 52 - 32 = 25 - 9 = 16
⇒ OL = 4
= \(\frac{1}{2}\) × 6 × 4m2
= \(\frac{1}{2}\) × 5 × BM = \(\frac{1}{2}\) × 6 × 4
⇒ BM = \(\frac{6 \times 4}{5}=\frac{24}{5}\)
Since, M is mid-point of BC, therefore
BC = 2BM = 2\(\left(\frac{24}{5}\right)\)m = \(\frac{48}{5}\)m = \(\frac{96}{10}\)m = 9.6m
Hence; the distance between Reshma and Mandip is 9.6 m.
Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distances on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Answer:
Let A, B and C be the places where the three boys are sitting and let ABC be an equilateral triangle of side 2x metres (see figure).
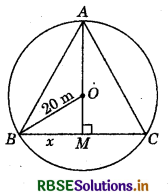
Clearly, BM = \(\frac{B C}{2}=\frac{2 x}{2}\) metres = x metres.
In right ∠d ∆ABM, AM2 = AB2 - BM2
= (2x)2 - x2 = 4x2 - x2 = 3x2
So, AM = √3x
Now, OM = AM - OA = (√3x - 20) m
In right ∠d AOBM, we have :
OB2 = BM2 + OM2
So, 202 = x2 + (√3 - 20)2
or 400 = x2 + 3x2 - 40√3x + 400
or 4x2 - 40 - √3 x = 0
or 4x(x - 10√3) = 0
Since, x ≠ 0, therefore
x - 10√3 = 0 or x = 10 - √3
Now, BC = 2BM = 2x = 20√3
Hence, the length of string of each phone is 20 - √3 m.

- RBSE Solutions for Class 9 Maths Chapter 6 रेखाएँ और कोण Ex 6.3
- RBSE Solutions for Class 9 Maths Chapter 14 सांख्यिकीEx 14.3
- RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5
- RBSE Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4
- RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.3
- RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.2
- RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.1
- RBSE Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.2
- RBSE Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1
- RBSE Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.3
- RBSE Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.2