RBSE Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.3

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.3 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.3

प्रश्न 1.
वृत्तों के कई जोड़े (युग्म) खींचिए। प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं ? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या है ?
हल:
नीचे प्रश्न के अनुसार विभिन्न वृत्तों के युग्मों को खींचा जा रहा है।

स्थिति - I यहाँ पर दोनों युग्मों में कोई बिन्दु उभयनिष्ठ नहीं है।

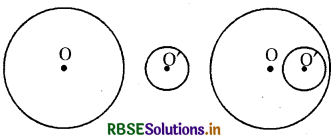
स्थिति-II दोनों युग्मों में केवल एक बिन्दु उभयनिष्ठ है।

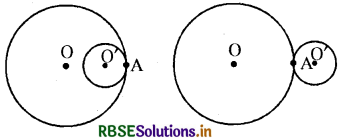
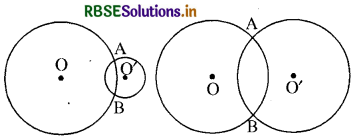
स्थिति-III
प्रत्येक युग्म में दो बिन्दु उभयनिष्ठ हैं अतः दो वृत्तों के उभयनिष्ठ बिन्दुओं की अधिकतम संख्या = 2 होगी।

प्रश्न 2.
मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।
हल:
रचना के पद

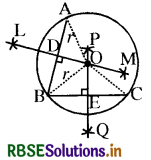
1. सर्वप्रथम वृत्त पर कोई तीन बिन्दु A, B और C लीजिए।
2. AB और BC को मिलाइए।
3. AB का लम्ब समद्विभाजक LM खींचिए। 4. BC का लंब समद्विभाजक PQ खींचिए।
4. माना कि LM और PQ बिन्दु O पर प्रतिच्छेद करते हैं। तब O  वृत्त का केन्द्र है।

सत्यापन
O, AB के लंब समद्विभाजक पर स्थित है।
∴ OA = OB .....(i)

O, BC के लम्ब समद्विभाजक पर स्थित है।
∴ OB = OC  .....(ii)

(i) और (ii) से हम देखते हैं कि
OA = OB = OC = r (माना)

तीन असरेख बिन्दु A, B और C वृत्त की परिधि स्थित बिन्दु 0 से बराबर दूरी (7) पर हैं। अतः, 0 वृत्त का केन्द्र है।

प्रश्न 3.
यदि दो वृत्त, परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित हैं।
हल:
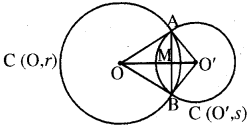
माना कि दो वृत्त C (O, r) और C (O', s) A और B पर प्रतिच्छेद करते हैं। हमें सिद्ध करना है कि 00' जीवा AB का लम्ब समद्विभाजक है। इसके लिए हम OA, OB, O'A और O'B को मिलाते हैं। त्रिभुजों OAO' और OBO' में,
OA = OB = r
O'A = O'B = s
और OO' = OO'

∴ ∆OAO' = ∆OBO' (सर्वांगसमता के नियम SSS के अनुसार)
∴ ∠AOO' = ∠BOO'
मान लीजिए AB और 00' का प्रतिच्छेदित बिन्दु M है। तब त्रिभुजों AOM और BOM में,
OA = OB
∠AOM = ∠BOM (:: ∠AOO' = ∠AOM और ∠BOO' = ∠BOM)
OM = OM
∴ Δ ΑΟΜ ≅ Δ BOM (सर्वांगसमता के नियम SAS के अनुसार)
AM = MB .....(i)
∠AMO = ∠BMO

अब, ∠AMO + ∠BMO = 180°
(रैखिक युग्म अभिगृहीत के अनुसार)

= ∠AMO + ∠AMO = 180°
⇒ 2∠AMO = 180°
⇒ ∠AMO = \(\frac{180^{\circ}}{2^{\circ}}\)
⇒ ∠AMO = 90°
साथ ही,
∠AMO = 90°
∠BMO = 90° (∵ ∠AMO = ∠BMO)

अब हमें प्राप्त है
AM = MB
∠AMO = ∠BMO = 90°
इससे सिद्ध होता है कि केन्द्रों 0 और 0' को मिलाने वाली रेखा उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित है।