RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.3

Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer:
The different pairs of circles are:

Clearly, these pairs may have 0 or 1 or 2 points in common.
Thus, a pair of circles cannot intersect each other at more than two points.

Question 2.
Suppose you are given a circle. Give a construction to find its centre.
Answer:
Steps of construction :

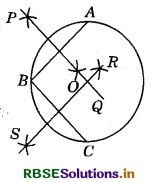
1. Take 3 points A, B and C on the circle.
2. Join AB and BC.
3. Draw PQ and RS, respectively the perpendicular bisectors, of AB and BC, which intersect each other at O. Then, 0 is the centre of the circle.

Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer:
Given : Two circles, with centres O and O' intersect at two points A and B so that AB is the common chord of the two circles and 00' is the line segment joining the centres of the two circles. Let 00' intersect AB at M.

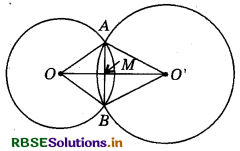
To prove: 00' is the perpendicular bisector of AB.
Construction: Draw line segments OA, OB, O'A and O'B.
Proof : In ∆s OAO' and OBO’, we have :
OA = OB    (Radii of the same circle)
O'A = O'B    (Radii of the same circle)
and, OO'    =    OO'    (Common)
∴ By SSS criterion of congruence, we have :
∆OAO' =    ∆OBO'
So, ∠AOO'    =    ∠BOO'    (CPCT)
or ∠AOM = ∠BOM ...........(1) (∵ ∠AOO' = ∠AOM and ∠BOO = ∠BOM)
In ∆s AOM and BOM, we have : 
OA = OB    (Radii of the same circle)
∠AOM = ∠BOM    [From (1)]
and, OM = OM    (Common)

By SAS criterion of congruence, we have :
∆AOM = ∆BOM
So, AM =BM and ∠AMO = ∠BMO
But ∠AMO + ∠BMO = 180°
2∠AMO = 180° or ∠AMO = 90°
Thus, AM =BM and ∠AMO = ∠BMO = 90°.
Hence, OO' is the perpendicular bisector of AB.