RBSE Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.2

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.2 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 10 वृत्त Ex 10.2

प्रश्न 1.
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।
हल:
कोई भी दो वृत्त सर्वांगसम तभी कहे जा सकते हैं जबकि उनमें से एक को दूसरे के ऊपर रखने पर वे एक-दूसरे को पूर्णतया ढक लें।
इस तथ्य को स्पष्टतः समझने के लिए हम मान लेते हैं कि C₁ (O₁, r) तथा C₂ (O₂, s) दो वृत्त हैं। अब वृत्त C₂ (O₂, s) को वृत्त C₁ (O₁, r) को ऊपर उठाकर इस प्रकार रखते हैं कि O₂, O, को पूर्णतः ढक ले। हम देखेंगे कि यदि r = s अर्थात् दोनों की त्रिज्याएँ यदि समान हैं तो वृत्त C₂ (O₂, s) वृत्त C₁ (O₁, r) को पूर्णतः ढक लेगा। अतः यह कहा जा सकता है कि दो वृत्त सर्वांगसम होते हैं, यदि उन वृत्तों की त्रिज्याएँ भी बराबर हों।
अब हम यह सिद्ध करेंगे कि दो सर्वांगसम वृत्तों की बराबर जीवाएँ केन्द्र पर बराबर कोण अन्तरित करती दिया है|
दो वृत्त C (O₁, r) तथा C (O₂, r) हैं जो सर्वांगसम हैं तथा जिनकी जीवाएँ क्रमशः PQ और RS हैं।
सिद्ध करना है- ∠PO₁Q = ∠RO₂S

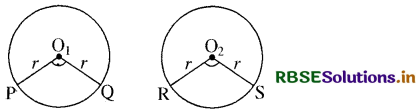
उपपत्ति-चित्रानुसार ∆ PO₁Q तथा ∆ RO₂S में
O₁P = O₁Q = O₂R = O₂S = r = (त्रिज्या)
PQ = RS (दिया है)
∴ ∆POQ ≅ ∆RO₂S
(सर्वांगसमता के नियम SSS के अनुसार)
अतः ∠PO₁Q = ∠RO₂S क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।

प्रश्न 2.
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं।
हल:
दिया है-दो सर्वांगसम वृत्त C (O₁, r) तथा C (O₂, r) हैं। उनमें दो जीवाएँ PQ तथा RS इस प्रकार हैं कि
∠PO₁Q = ∠RO₂S

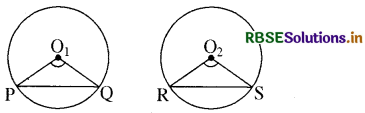
सिद्ध करना है- PQ = RS
उपपत्ति-वृत्तों में बने ∆PO₁Q तथा ∆RO₂S में
O₁P = O₁Q = O₂R = O₂S = r (त्रिज्याएँ)
∠PO₁Q = ∠RO₂S (दिया है)
∴ ∆PO₁Q ≅ ∆RO₂S
(सर्वांगसमता के नियम SAS के अनुसार)
अतः PQ = RS
(क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं)