RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.2

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 10 Circles Ex 10.2 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 10 Circles Ex 10.2

Question 1.
Recall that two circles are congruent, if they have the saine radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer:

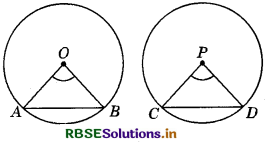
Given : AB and CD are two equal chords of two congruent circles with respective centres at O and P.

Question 2.
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer:

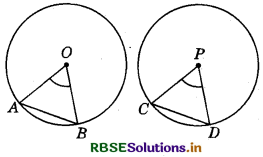
Given : AB and CD are two chords of congruent circles such that angles subtended by these chords at the respective centres O and P of the circles are equal.
i. e. ∠AOB = ∠CPD 
To prove : AB = CD
Proof : In ∆s AOB and CPD, we have :
AO = CP (Radii of the congruent circles)
BO = DP (Radii of the congruent circles) and,
∠AOB = ∠CPD    (Given)
By SAS criterion of congruence, we have :
∆AOB ≅ ∆CPD
So, AB = CD