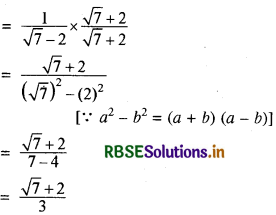RBSE Solutions for Class 9 Maths Chapter 1 संख्या पद्धति Ex 1.5

Rajasthan Board RBSE Solutions for Class 9 Maths Chapter 1 संख्या पद्धति Ex 1.5 Textbook Exercise Questions and Answers.

RBSE Class 9 Maths Solutions Chapter 1 संख्या पद्धति Ex 1.5

प्रश्न 1.
बंताइए नीचे दी गई संख्याओं में कौन-कौन परिमेय हैं और कौन-कौन अपरिमेय हैं
(i) 2 - √5
उत्तर:
2 - √5
हम जानते हैं कि एक परिमेय तथा अपरिमेय संख्या का अन्तर सदा ही अपरिमेय संख्या होता है। दी गई संख्या में 2 एक परिमेय संख्या है जिसमें से √5 अपरिमेय संख्या को घटाना है। घटाने पर निश्चित ही एक अपरिमेय संख्या प्राप्त होगी अर्थात् 2 - √5 = अपरिमेय संख्या

(ii) (3 + √23) - √23
उत्तर:
(3 + √23) - √23
= 3 + √23 - √23 = 3 = एक परिमेय संख्या अर्थात् दी गई संख्या एक परिमेय संख्या है।

(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
उत्तर:
\(\frac{2 \sqrt{7}}{7 \sqrt{7}}\) = एक परिमेय संख्या अर्थात् दी गई संख्या एक परिमेय संख्या है।

(iv) \(\frac{1}{\sqrt{2}}\)
उत्तर:
\(\frac{1}{\sqrt{2}}\) दी गई संख्या \(\frac{1}{\sqrt{2}}\) में 1 परिमेय संख्या है तथा √2 एक अपरिमेय संख्या है। हम जानते हैं कि शून्येतर परिमेय संख्या तथा एक अपरिमेय संख्या का भागफल सदैव एक अपरिमेय संख्या होता है। अत: दी गई संख्या एक अपरिमेय संख्या है।

(v) 2π
उत्तर:
2π, इस दी गई संख्या में 2 एक परिमेय संख्या है तथा 7 एक अपरिमेय संख्या है। हम जानते हैं कि एक शून्येतर परिमेय संख्या तथा एक अपरिमेय संख्या का गुणनफल सदैव ही एक अपरिमेय संख्या होता है। अतः दी गई संख्या एक अपरिमेय संख्या है।

प्रश्न 2.
निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए
(i) (3 + √3)(2+ √2)
हल:
(3 + √3)(2 + √2)
= 3 × 2 + 3 - 2 + 2√3 + √3 × √2
= 6 + 3√2 + 2√3 + √6

(ii) (3 + √3)(3 - √5)
हल:
(3 + √3)(3 - √3)
= 3 × 3 - 3√3 + 3√3 - √3 × √3
= 9 - 3 = 6

(iii) (√5 + √2)²
हल:
(√5 + √2)²
= (√5)² + (√2)² + 2√5 × √2
[सूत्र (a + b)² = a² + b² + 2ab के अनुसार]
= 5 + 2 + 2√10
= 7 + 2√10

(iv) (√5 - √2)(√5 + √2)
हल:
(√5 - √2) (√5 + √2)
= (√5)² - (√2)²
[सूत्र (a - b) (a + b) = a² - b² के अनुसार]
= 5 - 2 = 3.

प्रश्न 3.
आपको याद होगा कि 1 को एक वृत्त की परिधि (मान लीजिए c) और उसके व्यास (मान लीजिए d) के अनुपात से परिभाषित किया जाता है, अर्थात् π = \(\frac{c}{d}\) है। इस तथ्य का अंतर्विरोध करता हुआ प्रतीत होता है कि π अपरिमेय है। इस अंतर्विरोध का निराकरण आप किस प्रकार करेंगे?
उत्तर:
इसका कोई अन्तर्विरोध नहीं है क्योंकि एक वृत्त की परिधि (c) तथा उसका व्यास (d) अपरिमेय होते हैं। इसका कारण यह है कि जब कभी भी एक स्केल से या किसी अन्य युक्ति से लम्बाई मापते हैं, तब केवल एक निकटतम परिमेय मान प्राप्त होता है। इसी कारण आप यह अनुभव नहीं कर पाते हैं कि c या d अपरिमेय हैं। यहाँ
π = \(\frac{c}{d}\)
अत: ए एक अपरिमेय संख्या है।

प्रश्न 4.
संख्या रेखा पर √9.3 को निरूपित कीजिए।
उत्तर:
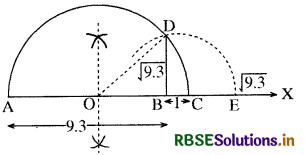
√9.3 को संख्या रेखा पर प्रदर्शित करने के लिए सर्वप्रथम एक दी हुई रेखा पर एक स्थिर बिन्दु A से 9.3 एकक की दूरी पर एक अन्य बिन्दु B अंकित किया अर्थात् अब AB = 9.3 एकक। बिन्दु B से 1 एकक की दूरी पर एक और बिन्दु C अंकित कर दिया। अब रेखा AC का समद्विभाग कर बिन्दु 0 ज्ञात कर लिया। अब O को केन्द्र मानकर OC के बराबर त्रिज्या लेकर एक अर्द्धवृत्त की रचना की। अब AC पर एक लम्ब रेखा खींचिए जो B से होकर जाए तथा अर्द्धवृत्त को बिन्दु D पर काटे। इस प्रकार प्राप्त BD = 19.3 है। केन्द्र B से BD त्रिज्या का चाप खींचा जो BX को E पर काटे। इस प्रकार प्राप्त BE संख्या रेखा पर √9.3 को निरूपित करता है।

गणितीय परिकलन:
∵ OA = OC = OD (अर्द्धवृत्त की त्रिज्या)
OA = OC = OD = \(\frac{1}{2}\)AC
=\(\frac{1}{2}\)[AB + BC]
[∵ AC = AB + BC]
= \(\frac{1}{2}\)[9.3 + 1.0]
= \(\frac{1}{2}\) × 10.3 = 5.15
अब पुनः समकोण त्रिभुज OBD से पाइथागोरस प्रमेय के अनुसार,
OB² + BD² = OD²
∴ BD² = OD² - OB²
= (OD - OB) (OD + OB)
[∵ a² - b² = (a - b) (a + b]
∴ BD = (OD - OB) (OD + OB)
= \(\sqrt{(5.15+4.15)(5.15-4.15)}\)
[∵ OB = OC - BC = 5.15 - 1 = 4.15]
∴ BD = \(\sqrt{9.3 \times 1}=\sqrt{9.3}\)

प्रश्न 5.
निम्नलिखित के हरों का परिमेयीकरण कीजिए-
(i) \(\frac{1}{\sqrt{7}}\)
हल:
\(\frac{1}{\sqrt{7}}\)
अंश व हर को √7 से गुणा करने पर
\(\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}=\frac{\sqrt{7}}{7}\)

(ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
हल:

(iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)
हल:
\(\frac{1}{\sqrt{5}+\sqrt{2}}\)
दी गई संख्या के अंश व हर में √5 - √2 से गुणा करने पर

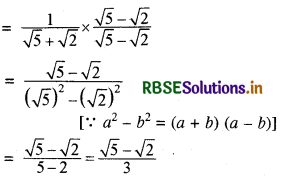
(iv) \(\frac{1}{\sqrt{7}-2}\)
हल:
\(\frac{1}{\sqrt{7}-2}\)
दी गई संख्या के अंश व हर में √7 + 2 से गुणा करने पर