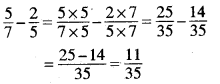RBSE Solutions for Class 6 Maths Chapter 7 भिन्न Intext Questions

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 7 भिन्न Intext Questions Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 7 भिन्न Intext Questions

(प्रयास कीजिए - पृष्ठ 150)

प्रश्न 1.
संख्या रेखा पर \(\frac{3}{5}\) को दर्शाइए। 
हल:
हम जानते हैं कि \(\frac{3}{5}\) है शून्य से बड़ा है और 1 से कम है। इसलिए इसे 0 से 1 के बीच होना चाहिए।
चूँकि हमें ३ को दर्शाना है, इसलिए हम 0 से 1 के बीच की दूरी को पाँच बराबर भागों में बाँटेंगे और 3 भाग को है \(\frac{3}{5}\) से दर्शायेंगे।

इस प्रकार, बिन्दु P भिन्न \(\frac{3}{5}\) को दर्शाता है।

प्रश्न 2.
संख्या रेखा पर \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) और \(\frac{10}{10}\) को दर्शाइए।
हल:
हम जानते हैं कि भिन्न \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) और \(\frac{10}{10}\) इस प्रकार हैं
0 ≤ \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10} \) और \(\frac{10}{10}\) ≤ 1

चूँकि हमें \(\frac{1}{10}, \frac{0}{10}, \frac{5}{10}\) और \(\frac{10}{10}\) को दर्शाना है, इसलिए हम 0 से 1 के बीच की दूरी को 10 बराबर भाग में बाँटते हैं। एक भाग को \(\frac{10}{10}\) से तथा 5 भाग को \(\frac{5}{10}\) से दर्शाते हैं।

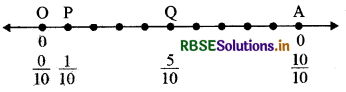
स्पष्ट है कि बिन्दु P और Q भिन्न \(\frac{1}{10}\) और \(\frac{5}{10}\) को दर्शाते हैं। 
\(\frac{0}{10}\) बिन्दु 0 है (जो बिन्दु 0 है) और \(\frac{10}{10}\) एक पूर्ण है (जो कि बिन्दु A है)।

प्रश्न 3.
क्या आप 0 और 1 के बीच कोई अन्य भिन्न को दर्शा सकते हैं? ऐसी पाँच भिन्न और लिखिए जिन्हें आप दर्शा सकते हैं और उन्हें संख्या रेखा पर दर्शाइए।
हल:
हाँ, हम 0 से 1 के बीच अन्य भिन्न को दर्शा सकते
\(\frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8}, \frac{5}{8}\), 5 ऐसे भिन्न हैं जिन्हें हम संख्या रेखा पर 
क्रमशः P, Q,R, S और T से निरूपित कर सकते हैं। जैसा कि दिया हुआ है

प्रश्न 4.
0 और 1 के बीच में कितनी भिन्न स्थित हैं? सोचिए, चर्चा कीजिए और अपने उत्तर को लिखिए।
हल:
चूँकि बिन्दुओं 0 से 1 के बीच संख्या रेखा पर असंख्य संख्याएँ हैं, इसलिए 0 से 1 के बीच अनगिनत भिन्न हैं।

(प्रयास कीजिए - पृष्ठ 151)

प्रश्न 1.
एक उचित भिन्न लिखिए
(a) जिसका अंश 5 और हर 7 है।
हल:
अभीष्ट भिन्न = \(\frac{5}{7}\)

(b) जिसका हर 9 है और अंश 5 है।
हल:
अभीष्ट भिन्न = \(\frac{5}{9}\)

(c) जिसके अंश और हर का योग 10 है। आप इस प्रकार की कितनी भिन्न लिख सकते हैं?
हल:
सम्भव युग्म जिनके अंश और हर का योग 10 है 1; 9; 2, 8; 3,7; 4, 6 जिनसे उचित भिन्न \(\frac{1}{9}, \frac{2}{8}, \frac{3}{7}\) और \(\frac{4}{6}\) है. और है हैं। इस प्रकार ऐसी चार भिन्न लिखी जा सकती हैं।

(d) जिसका हर उसके अंश से 4 अधिक है। (कोई पाँच भिन्न बनाइए। आप और कितनी भिन्न बना सकते हैं?)
हल:
5 ऐसी भिन्न जिनके हर उनके अंश से 4 अधिक हैं1 2 3 4 5 हम दी हुई परिस्थिति के अनुसार उचित भिन्नों की असंख्य संख्याएँ बना सकते हैं।

प्रश्न 2.
एक भिन्न दी हुई है। इसे देखकर, आप कैसे बता सकते हैं कि यह भिन्न
(a) 1 से छोटी है?
(b) 1 के बराबर है?
हल:
(a) किसी भिन्न में यदि अंश उसके हर से छोटा है तो भिन्न 1 से छोटी है।
(b) किसी भिन्न में यदि अंश हर के बराबर है तो भिन्न 1 के बराबर है। 

प्रश्न 3.
संकेत '>', '<' या '=' का प्रयोग करके रिक्त स्थानों को भरिएहल
(a) \(\frac{1}{2}\) ___ 1
हल:
<

(b) \(\frac{3}{5}\) _____ 1
हल:
<

(c) 1 ____ \(\frac{7}{8}\)
हल:
>

(d) \(\frac{4}{2}\) _____ 1
हल:
=

(e) \(\frac{0}{0}\) ____ 1
हल:
<

(f) \(\frac{2005}{2005}\) _______ 11 
हल:
=

(प्रयास कीजिए - पृष्ठ 15)

प्रश्न 1.
क्या \(\frac{1}{3}\) और \(\frac{2}{7}\) ; \(\frac{2}{5}\) और \(\frac{2}{7}\) तथा \(\frac{2}{9}\) और \(\frac{6}{27}\) तुल्य भिन्न हैं? कारण दीजिए।
हल:
-\(\frac{1}{3}\) और \(\frac{2}{7}\) है:

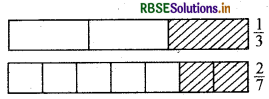
स्पष्ट रूप से, आकृतियाँ समान आकार की हैं किन्तु छायांकित हिस्सा आकृति का बराबर हिस्सा निरूपित नहीं करता है।
इसलिए \(\frac{1}{3}\) और \(\frac{2}{7}\) तुल्य भिन्नै नहीं हैं। है और

\(\frac{2}{5}\) और \(\frac{2}{7}\):

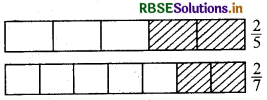
स्पष्ट रूप से, आकृतियाँ समान आकार की हैं किन्तु छायांकित हिस्सा आकृति का बराबर भाग निरूपित नहीं करता है।
इसलिए है \(\frac{2}{5}\) और \(\frac{2}{7}\) तुल्य भिन्नै नहीं हैं।

\(\frac{2}{9}\) और \(\frac{6}{27}\)

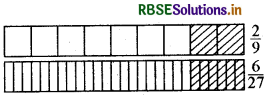
स्पष्ट रूप से, इन आकृतियों का समान आकार है तथा छायांकित हिस्सा भी आकृति का बराबर भाग दिखाता है। अतः \(\frac{2}{9}\) और \(\frac{6}{27}\) तुल्य भिन्नें हैं। 

प्रश्न 2.
चार तुल्य भिन्नों का एक अन्य उदाहरण दीजिए।
हल:

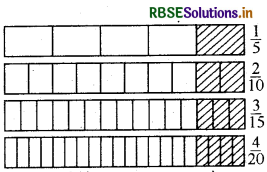
स्पष्टतः इन आकृतियों का समान आकार है तथा छायांकित हिस्सा आकृति का बराबर भाग निरूपित करता है। 
अत: \(\frac{1}{5}, \frac{2}{10}, \frac{3}{15}\) और \(\frac{4}{20}\) चारों तुल्य भिन्नें हैं।

प्रश्न 3.
प्रत्येक भिन्न को पहचानिए। क्या ये भिन्ने तुल्य
हल:
ये भिन्नै \(\frac{6}{8}, \frac{9}{12}, \frac{12}{16}\) और \(\frac{15}{20}\) हैं। 

स्पष्टतः इन आकृतियों का समान आकार है तथा छायांकित भाग आकृति का बराबर हिस्सा दिखाता है।
इसलिए \(\frac{6}{8}, \frac{9}{12}, \frac{12}{16}\) और \(\frac{15}{20}\) तुल्य भिन्नें हैं।

(प्रयास कीजिए - पृष्ठ 156)

प्रश्न 1.
निम्नलिखित में से प्रत्येक की पाँच तुल्य भिन्न ज्ञात कीजिए
(i) \(\frac{2}{3}\)
हल:

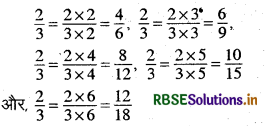
अतः, \(\frac{2}{3}\) की पाँच तुल्य भिन्न है \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}\) और \(\frac{12}{18}\)

(ii) \(\frac{1}{5}\)
हल:

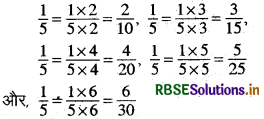
अतः, \(\frac{1}{5}\) की पाँच तुल्य भिन्न हैं-\(\frac{2}{10}, \frac{3}{15}, \frac{4}{20}, \frac{5}{25}\) और \(\frac{12}{18}\)

(iii) \(\frac{3}{5}\)
हल:

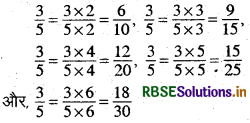
और, \(\frac{3}{5}\) अत:, 3 की पाँच तुल्य भिन्न हैं-\(\frac{6}{10}, \frac{9}{15}, \frac{12}{20}, \frac{15}{25}\) और \(\frac{6}{30}\)

(iv) \(\frac{5}{8}\)
हल:

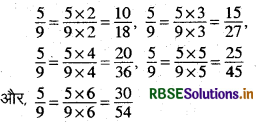
अतः, \(\frac{5}{8}\) की पाँच तुल्य भिन्न हैं-\(\frac{10}{18}, \frac{15}{27}, \frac{20}{36}, \frac{25}{45}\) और \(\frac{30}{54}\)

(प्रयास कीजिए - पृष्ठ 159)

प्रश्न 1.
निम्न को सरलतम रूप में लिखिए
(i) \(\frac{15}{75}\)
(ii) \(\frac{16}{72}\)
(iii) \(\frac{17}{51}\)
(iv) \(\frac{42}{28}\)
(v) \(\frac{80}{24}\)
हल:
किसी भिन्न को सरलतम रूप में लिखने के लिए उस भिन्न के अंश और हर का म.स. निकालकर फिर अंश और हर दोनों में इस म.स. से भाग दे दिया जाता है।
(i) \(\frac{15}{75}\) पहले हम 15 तथा 75 का महत्तम समापवर्तक निकालेंगे।

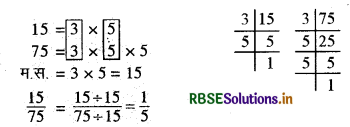
(ii) \(\frac{16}{72}\) : 16 तथा 72 का म.स. 8 है।
∴ \(\frac{16}{72}=\frac{16 \div 8}{72 \div 8}=\frac{2}{9}\)

(iii) \(\frac{17}{51}\) : 17 तथा 51 का म.स. है = 17
∴ \(\frac{17}{51}=\frac{17 \div 17}{51 \div 17}=\frac{1}{3}\)

(iv) \(\frac{42}{28}\) : 42 तथा 28 का म.स. 14 है। 
∴ \(\frac{42}{28}=\frac{42 \div 14}{28 \div 14}=\frac{3}{2}\)

(v) \(\frac{80}{24}\) : 80 तथा 24 का म.स. है
∴ \(\frac{80}{24}=\frac{80 \div 8}{24 \div 8}=\frac{10}{3}\)

प्रश्न 2.
क्या है, \(\frac{49}{64}\) अपने सरलतम रूप में है? 
हल:
कोई भिन्न अपने सरलतम रूप में तब होती है जब उसके अंश तथा हर में 1 के अतिरिक्त कोई अन्य उभयनिष्ठ गुणनखण्ड न हो। हमारी भिन्न है ।

अतः 49 = 7 × 7 × 1 
और 64 = 2 × 2 × 2 × 2 × 2 × 2 × 1 
∴ 49 तथा 64 का म.स. = 1 
अतः \(\frac{49}{64}\) अपने सरलतम रूप में है। 

(प्रयास कीजिए - पृष्ठ 161)

प्रश्न 1.
आप जूस की बोतल का \(\frac{1}{5}\) वाँ भाग प्राप्त करते हैं और आपकी बहन को उस बोतल का एक-तिहाई भाग मिलता है। किसको अधिक जूस मिलता है?
हल:
हम \(\frac{1}{5}\) तथा \(\frac{1}{3}\) की तुलना करना चाहते हैं
\(\frac{1}{5}=\frac{1 \times 3}{5 \times 3}=\frac{3}{15} \) और \(\frac{1}{3}=\frac{1 \times 5}{3 \times 5}=\frac{5}{15}\)
क्योंकि 5 > 3, इसलिए \(\frac{5}{15}>\frac{3}{15}\) अर्थात् \(\frac{5}{15}>\frac{3}{15}\)
इस प्रकार बहन को ज्यादा जूस मिलता है।

(प्रयास कीजिए - पृष्ठ 162)

प्रश्न 1.
कौन-सी भिन्न बड़ी है? 
(i) \(\frac{7}{10}\) या \(\frac{8}{10}\)
(ii) \(\frac{11}{24}\) या \(\frac{13}{24}\)
(ii) \(\frac{17}{102}\) या \(\frac{12}{102}\)
ऐसी भिन्नों की तुलना करना क्यों सरल है?
हल:
हम जानते हैं कि वे भिन्नै जिनका हर बराबर हो, उनमें जितना बड़ा अंश होगा, उस भिन्न का मान उतना ही बड़ा होगा। अतः दी गई भिन्नें
(i) \(\frac{8}{10}>\frac{7}{10}\)
(ii) \(\frac{13}{24}>\frac{11}{24}\)
(ii) \(\frac{17}{102}>\frac{12}{102}\)
ऐसी भिन्नों की तुलना आसान है क्योंकि इन स्थितियों में केवल अंशों की तुलना की जाती है। 

प्रश्न 2.
निम्न को आरोही क्रम में लिखिए और साथ ही अवरोही क्रम में भी लिखिए
(a) \(\frac{1}{8}, \frac{5}{8}, \frac{3}{8}\)
हल:
हम जानते हैं कि भिन्नै जिनका हर बराबर हो, उनमें जितना बड़ा अंश होगा, उस भिन्न का मान उतना ही बड़ा होगा। अतः दी गई भिन्नें
आरोही क्रम : \(\frac{1}{8}, \frac{3}{8}, \frac{5}{8}\)
अवरोही क्रम : \(\frac{5}{8}, \frac{3}{8}, \frac{1}{8}\)

(b) \(\frac{1}{5}, \frac{11}{5}, \frac{4}{5}, \frac{3}{5}, \frac{7}{5}\)
हल:
आरोही क्रम : \(\frac{1}{5}, \frac{3}{5}, \frac{4}{5}, \frac{7}{5}, \frac{11}{5}\)
अवराहा क्रम : \(\frac{11}{5}, \frac{7}{5}, \frac{4}{5}, \frac{3}{5}, \frac{1}{5}\)

(c) \(\frac{1}{5}, \frac{11}{5}, \frac{4}{5}, \frac{3}{5}, \frac{7}{5}\)
हल:
आरोही क्रम : \(\frac{1}{7}, \frac{3}{7}, \frac{7}{7}, \frac{11}{7}, \frac{13}{7}\)
अवरोही क्रम : \(\frac{13}{7}, \frac{11}{7}, \frac{7}{7}, \frac{3}{7}, \frac{1}{7}\)

(प्रयास कीजिए - पृष्ठ 164)

प्रश्न 1.
निम्नलिखित भिन्नों को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए
(a) \(\frac{1}{12}, \frac{1}{23}, \frac{1}{5}, \frac{1}{7}, \frac{1}{50}, \frac{1}{9}, \frac{1}{17}\)
हल:
ऐसी भिन्नै जिनका अंश बराबर हो, उनमें जितना बड़ा हर होगा, उस भिन्न का मान उतना ही छोटा होगा। अतः दी गई भिन्नें इस प्रकार हैं
आरोही क्रम : \(\frac{1}{50}, \frac{1}{23}, \frac{1}{17}, \frac{1}{12}, \frac{1}{9}, \frac{1}{7}, \frac{1}{5}\)
अवरोही क्रम : \(\frac{1}{5}, \frac{1}{7}, \frac{1}{9}, \frac{1}{12}, \frac{1}{17}, \frac{1}{23}, \frac{1}{50}\)

(b) \(\frac{3}{7}, \frac{3}{11}, \frac{3}{5}, \frac{3}{2}, \frac{3}{13}, \frac{3}{4}, \frac{3}{17}\)
हल:
आरोही क्रम : \(\frac{3}{17}, \frac{3}{13}, \frac{3}{11}, \frac{3}{7}, \frac{3}{5}, \frac{3}{4}, \frac{3}{2}\)
अवरोही क्रम : \(\frac{3}{2}, \frac{3}{4}, \frac{3}{5}, \frac{3}{7}, \frac{3}{11}, \frac{3}{13}, \frac{3}{17}\)

(c) उपरोक्त प्रकार के तीन और उदाहरण लिखिए तथा उन्हें आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।
हल:
तीन और उदाहरण निम्न प्रकार हैं

(प्रयास कीजिए - पृष्ठ 168)

प्रश्न 1.
मेरी माँ ने एक सेब को चार बराबर भागों में बाँटा। उन्होंने मुझे 2 भाग और मेरे भाई को एक भाग दिया। उन्होंने हम दोनों को कुल सेब का कितना भाग दिया?
हल:
सेब को चार बराबर भागों में बाँटा गया अर्थात् प्रत्येक भाग \(\frac{1}{4}\) होगा। 
मुझे दिया गया 2 भाग = \(\frac{2}{4}\) 
मेरे भाई को दिया गया 1 भाग = \(\frac{1}{4}\) 
∴ हम दोनों को सेब का कुल भाग दिया गया
= \(\frac{2}{4}+\frac{1}{4}\)
= \(\frac{2}{4}+\frac{1}{4}\)

प्रश्न 2.
माँ ने नीलू और उसके भाई को गेहूँ में से कंकड़ बीनने के लिए कहा। नीलू ने कुल कंकड़ों का \(\frac{1}{4}\) कंकड़ बीने और उसके भाई ने भी कुल कंकड़ों के \(\frac{1}{4}\) कंकड़ बीने। दोनों ने मिलकर कुल कंकड़ों की कितनी भिन्न बीनी? 
हल:
नीलू और उसके भाई प्रत्येक ने \(\frac{1}{4}\) भाग बीना। 
दोनों ने मिलकर कुल कंकड़ बीने
= \(\frac{1}{4}+\frac{1}{4}=\frac{1+1}{4}=\frac{2}{4}=\frac{1}{2}\)

प्रश्न 3.
सोहन अपनी अभ्यास पुस्तिका पर कवर चढ़ा रहा था। उसने सोमवार को \(\frac{1}{4}\) भाग पर कवर चढ़ा लिया। मंगलवार को उसने अन्य \(\frac{1}{4}\) भाग पर कवर चढा लिया और शेष बुधवार को। बुधवार को उसने कवर का कौन-सा भाग चढ़ाया?
हल:
सोमवार को सोहन द्वारा चढ़ाया गया कवर = \(\frac{1}{4}\) भाग
उसके द्वारा मंगलवार को चढ़ाया गया कवर = \(\frac{1}{4}\)
शेष कवर बुधवार को चढ़ाया।। 
∴ सोहन द्वारा बुधवार को चढ़ाया गया कवर का भाग
= 1 - \(\frac{1}{4}-\frac{1}{4}=\frac{4}{4}-\frac{1}{4}-\frac{1}{4}\)
= \(\frac{4-1-1}{4}=\frac{2}{4}=\frac{1}{2}\)भाग

(प्रयास कीजिए - पृष्ठ 170-I)

प्रश्न 1.
आकृतियों की सहायता से जोड़िए
(i) \(\frac{1}{8}+\frac{1}{8}\)
हल:
एक 4 × 2 विमाओं का कागज लेंगे। कागज में लम्बाई के अनुसार एक पंक्ति में चार वर्ग और चौड़ाई के अनुदिश दो वर्ग खानों में लेंगे। एक वर्ग को छायांकित करेंगे और एक दूसरे वर्ग को पुनः ऊर्ध्वाधर छायांकित करेंगे। 

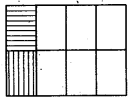
आकृति से स्पष्ट है =\(\frac{1}{8}+\frac{1}{8}=\frac{2}{8}=\frac{1}{4}\)

(ii) \(\frac{2}{5}+\frac{3}{5}\)
हल:
पाँच खाने लेंगे। इनमें से दो वर्गों को छायांकित करके 3 वर्गों को ऊर्ध्वाधर छायांकित करेंगे। 

आकृति से स्पष्ट है = \(\frac{2}{5}+\frac{3}{5}=\frac{5}{5}\) = 1

(iii) \(\frac{1}{12}+\frac{1}{12}+\frac{1}{12}\)
हल:
4 × 3 वर्ग लेंगे। एक खाने को तिरछा छायांकित करेंगे और 1 खाने को क्षैतिज रूप में और 1 खाने को ऊर्ध्वाधर छायांकित करेंगे। आकृति से स्पष्ट है

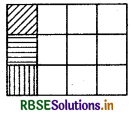
= \(\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{12}=\frac{1}{4}\)

प्रश्न 2.
\(\frac{1}{12}+\frac{1}{12}\) को जोड़ने पर हम क्या प्राप्त करते हैं? आप चित्र रूप में इस कैसे दर्शा सकते हो? कागज मोड़ने की क्रिया द्वारा कैसे दर्शाया जा सकता है?
हल:
\(\frac{1}{12}+\frac{1}{12}=\frac{1+1}{12}=\frac{2}{12}=\frac{1}{6}\)
चित्र रूप में प्रदर्शन

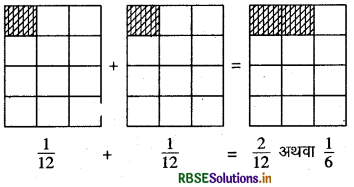
इसलिए \(\frac{1}{12}+\frac{1}{12}=\frac{2}{12}=\frac{1}{6}\)
[नोट-कागज मोड़कर स्वयं बनायें।] .

प्रश्न 3.
प्रश्न 1 और 2 जैसे पाँच और प्रश्न बनाइए। अपने मित्रों के साथ उन्हें. हल कीजिए।
हल:
[नोट-स्वयं कीजिए।] 

(प्रयास कीजिए - पृष्ठ 170-II)

प्रश्न 1.
\(\frac{7}{8}\) और \(\frac{3}{8}\) का अन्तर ज्ञात कीजिए।
हल:
= \(\frac{7}{8}-\frac{3}{8}=\frac{7-3}{8}=\frac{4}{8}=\frac{1}{2}\)

प्रश्न 2.
माँ ने एक गुड़ की पट्टी गोल आकृति में बनाई। उसने उसे 5 बराबर भागों में विभाजित किया। सीमा ने उसमें से एक टुकड़ा खा लिया। यदि मैं एक अन्य टुकड़ा खा लूँ, तो कितनी गुड़ की पट्टी शेष रहेगी?
हल:
माँ ने गोल आकार में गुड़ की पट्टी को 5 बराबर  भागों में बाँटा । इसलिए प्रत्येक भाग = \(\frac{1}{5}\)
सीमा ने गुड़ की पट्टी का भाग खाया = \(\frac{1}{5}\)
मेरे द्वारा गुड़ की पट्टी का खाया जाने वाला भाग = \(\frac{1}{5}\)
गुड़ की पट्टी का शेष भाग = 1 - \(\frac{1}{5}-\frac{1}{5} \)
= \(\frac{5}{5}-\frac{1}{5}-\frac{1}{5}\) [∵ 1 = \(\frac{5}{5}\)]
= \(\frac{5-1-1}{5}=\frac{3}{5}\)

प्रश्न 3.
मेरी बड़ी बहन ने एक तरबूज को 16 बराबर भागों में विभाजित किया। मैंने इसके 7 टुकड़े खा लिए। मेरे मित्र ने 4 टुकड़े खाए। हमने मिलकर कुल कितना तरबूज खाया? मैंने अपने मित्र से कितना अधिक तरबूज खाया? कितना तरबूज शेष रह गया? 
हल:
एक तरबूज को मेरी बड़ी बहन ने 16 बराबर भागों में बाँटा। इसलिए प्रत्येक भाग = \(\frac{1}{16} \)
मेरे द्वारा तरबूज का खाया भाग = \(\frac{7}{16} \)
मेरे मित्र द्वारा तरबूज का खाया भाग = \(\frac{4}{16}\)

हम दोनों द्वारा खाया गया तरबूज का भाग
= \(\frac{7}{16}+\frac{4}{16}=\frac{7+4}{16}=\frac{11}{16}\)

मेरे द्वारा खाया गया अधिक भाग
= \(\frac{7}{16}-\frac{4}{16}=\frac{7-4}{16}=\frac{3}{16}\)

बचा हुआ तरबूज = 1 - \(\frac{11}{16}=\frac{16}{16}-\frac{11}{16}\) [∵ 1 = \(\frac{16}{16}\)]
= \(\frac{5}{16}\)

प्रश्न 4.
इसी प्रकार के पाँच प्रश्न और बनाइए और अपने मित्रों के साथ इन्हें कीजिए।
हल:
[नोट-स्वयं कीजिए।]

(प्रयास कीजिए - पृष्ठ 173)

प्रश्न 1.
\(\frac{2}{5}\) और \(\frac{3}{7}\) को जोड़िए।
हल:
\(\frac{2}{5}+\frac{3}{7}\)
5 तथा 7 का लघुत्तम समापवर्त्य = 5 × 7 = 35
अब हर 5 तथा 7 को 35 में बदलें

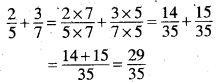
प्रश्न 2.
\(\frac{5}{7}\) में से \(\frac{2}{5}\) को घटाइए।
हल:
\(\frac{5}{7}-\frac{2}{5}\)
7 तथा 5 का ल.स. = 7 × 5 = 35 
अब हर 7 तथा 5 को 35 में बदलें