RBSE Solutions for Class 6 Maths Chapter 7 भिन्न Ex 7.3

Rajasthan Board RBSE Solutions for Class 6 Maths Chapter 7 भिन्न Ex 7.3 Textbook Exercise Questions and Answers.

RBSE Class 6 Maths Solutions Chapter 7 भिन्न Ex 7.3

प्रश्न 1.
प्रत्येक चित्र में छायांकित भागों के लिए भिन्न लिखिए। क्या ये सभी भिन्न तुल्य हैं?

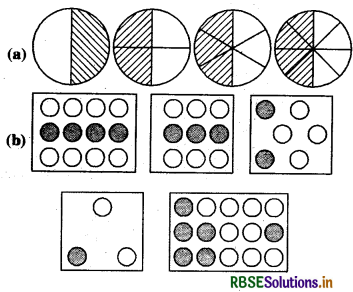
हल:
(a) चित्रों में छायांकित भागों के लिए भिन्न हैं 128 और है
\(\frac{1}{2}, \frac{2}{4}, \frac{3}{6}\) और \(\frac{4}{8}\)

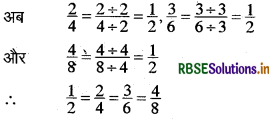
अर्थात्, सभी भिन्न तुल्य हैं। | 

(b) चित्रों में छायांकित भागों के लिए भिन्न हैं
\(\frac{4}{12}, \frac{3}{9}, \frac{2}{6}, \frac{1}{3}\) और \(\frac{6}{15}\)

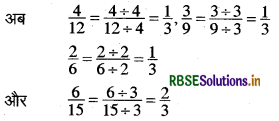
इसलिए \(\frac{4}{12}, \frac{3}{9}, \frac{2}{6}, \frac{1}{3}\) और \(\frac{6}{15}\) तुल्य भिन्न नहीं हैं।

प्रश्न 2. 
छायांकित भागों के लिए भिन्नों को लिखिए और प्रत्येक पंक्ति में से तुल्य भिन्नों को चुनिए।

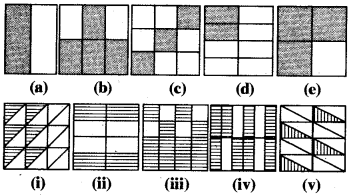
हल:
दी गई आकृतियों द्वारा दर्शाई गई भिन्नें इस प्रकार हैं

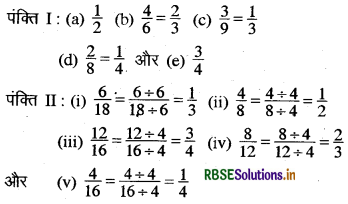
पंक्ति I तथा पंक्ति II से तुल्य भिन्नों के जोड़े बनाने पर
(a) (ii), (b) (iv), (c) (i), (d) (v) और (e) (iii)

प्रश्न 3.
निम्न में से प्रत्येक में को सही संख्या से प्रतिस्थापित कीजिए
हल:

प्रश्न 4.
\(\frac{3}{5}\) के तुल्य वह भिन्न ज्ञात कीजिए जिसका
(a) हर 20 है
(b) अंश 9 है
(c) हर 30 है
(d) अंश 27 है
हल:
(a) ∵ 20 ÷ 5 = 4 
∴ हम \(\frac{3}{5}\) के अंश तथा हर को चार से गुणा करते हैं
\(\frac{3}{5}=\frac{3 \times 4}{5 \times 4}=\frac{12}{20}\)

(b) ∵9 ÷ 3 = 3
∴ हम \(\frac{3}{5}\) के अंश तथा हर को 3 से गुणा करते हैं
\(\frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\)

(c) ∵ 30 ÷ 5 = 6
∴ हम \(\frac{3}{5}\) के अंश तथा हर को 6 से गुणा करते हैं
\(\frac{3}{5}=\frac{3 \times 6}{5 \times 6}=\frac{18}{30}\)

(d) ∵ 27 ÷ 3 = 9 
∴ हम \(\frac{3}{5}\) के अंश तथा हर को 9 से गुणा करते हैं
\(\frac{3}{5}=\frac{3 \times 9}{5 \times 9}=\frac{27}{45}\)

प्रश्न 5.
\(\frac{36}{48}\) के तुल्य वह भिन्न ज्ञात कीजिए जिसका
(a) अंश 9 है
(b) हर 4 है
हल:
(a) ∵ 36 ÷ 9 = 4
∴ हम \(\frac{36}{48}\) के अंश तथा हर को 4 से भाग करते हैं. 
\(\frac{36}{48}=\frac{36 \div 4}{48 \div 4}=\frac{9}{12}\)

(b) ∵ 48 ÷ 4 = 12 
∴ हम 10 के अंश तथा हर को 12 से भाग करते हैं
\(\frac{36}{48}=\frac{36 \div 12}{48+12}=\frac{3}{4}\)

प्रश्न 6.
जाँच कीजिए कि निम्न भिन्न तुल्य हैं या नहीं
(a) \(\frac{5}{9}, \frac{30}{54}\)
हल:

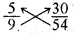
5 × 54 = 270 और 9 × 30 = 270
∴ 5 × 54 = 9 × 30
इसलिए , तथा 34 तुल्य भिन्न हैं।

(b) \(\frac{3}{10}, \frac{12}{50}\)
हल:

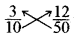
3 × 50 = 150 और 10 × 12 = 120 
∴ 3 × 50 ≠ 10 × 12
इसलिए \(\frac{3}{10}\) और \(\frac{12}{50}\) तुल्य भिन्न नहीं हैं। 

(c) \(\frac{7}{13}, \frac{5}{11}\)
हल:

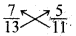
7 × 11 = 77 और. 13 × 5 = 65 
∴ 7 × 11 ≠ 13 × 5
इसलिए \(\frac{7}{13}\) और \(\frac{5}{11}\) में तुल्य भिन्न नहीं हैं।

प्रश्न 7. 
निम्नलिखित भिन्नों को उनके सरलतम रूप में बदलिए
(a) \(\frac{48}{60}\)
हल:
\(\frac{48}{60}\) को सरलतम रूप में बदलने के लिए हम 48 तथा 60 का महत्तम समापवर्तक निकालते हैं

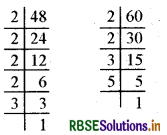
∴ 48 = 2 × 2 × 2 × 2 × 3, 60 = 2 × 2 × 3 × 5 
∴ 48 और 60 का म.स. = 2 × 2 × 3 = 12 
इसलिए, \(\frac{48}{60}=\frac{48 \div 12}{60 \div 12}=\frac{4}{5}\)

(b) \(\frac{150}{60}\)
हल:
\(\frac{150}{60}\) को सरलतम रूप में बदलने के लिए हम 150 और 60 का महत्तम समापवर्तक निकालते हैं। 
150 और 60 का म.स. = 30 
इसलिए, \(\frac{150}{60}=\frac{150 \div 30}{60 \div 30}=\frac{5}{2}\)

(c) \(\frac{84}{98}\)
हल:
\(\frac{84}{98}\) को सरलतम रूप में बदलने के लिए हम 84 और 98 का महत्तम समापवर्तक निकालते हैं। 
84 और 98 का म.स. = 14
इसलिए, \(\frac{84}{98}=\frac{84 \div 14}{98 \div 14}=\frac{6}{7}\)

(d) \(\frac{12}{52}\)
हल:
\(\frac{12}{52}\) को सरलतम रूप में बदलने के लिए हम 12 और 52 का महत्तम समापवर्तक निकालते हैं।
12 और 52 का म.स. = 4 
इसलिए, \(\frac{12}{52}=\frac{12 \div 4}{52 \div 4}=\frac{3}{13}\)

(e) \(\frac{7}{28}\)
\(\frac{7}{28}\) को सरलतम रूप में बदलने के लिए हम 7 और 28 का महत्तम समापवर्तक निकालते हैं। 
7 और 28 का म.स. = 7 
इसलिए, \(\frac{7}{28}=\frac{7 \div 7}{28 \div 7}=\frac{1}{4}\)

प्रश्न 8.
रमेश के पास 20 पेंसिल थीं। शीलू के पास 50 पेंसिल और जमाल के पास 80 पेंसिल थीं। 4 महीने के बाद, रमेश ने 10 पेंसिल प्रयोग कर ली, शीलू ने 25 पेंसिल प्रयोग कर ली और जमाल ने 40 पेंसिल प्रयोग कर लीं। प्रत्येक ने अपनी पेंसिलों की कौन-सी भिन्न प्रयोग कर ली? जाँच कीजिए कि प्रत्येक ने अपनी पेंसिलों की समान भिन्न प्रयोग की है।
हल:
रमेश, शीलू तथा जमाल द्वारा प्रयोग किए जाने वाली पेंसिल का हिस्सा क्रमशः 10.30 और 40 है। 

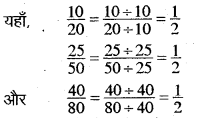
इसलिए इनमें से प्रत्येक ने अपनी पेंसिल की बराबर भिन्न प्रयोग की।

प्रश्न 9.
तुल्य भिन्नों का मिलान कीजिए और प्रत्येक के लिए दो भिन्न और लिखिए

हल:
(i) \(\frac{250}{400}\) का सरलतम रूप
250 तथा 400 का महत्तम समापवर्तक है = 50 
इसलिए \(\frac{250}{400}=\frac{250 \div 50}{400 \div 50}=\frac{5}{8}\)
इसलिए (i) का मिलान (d) से हुआ। 

दो अन्य तुल्य भिन्न हैं
\(\frac{5 \times 2}{8 \times 2}\) और \(\frac{5 \times 3}{8 \times 3}\) यानी \(\frac{10}{16}\) और \(\frac{15}{24}\)

(ii) \(\frac{180}{200}\) का सरलतम रूप 180 और 200 का म.स. = 20 
इसलिए \(\frac{180}{200}=\frac{180 \div 20}{200 \div 20}=\frac{9}{10}\)
इसलिए (ii) का मिलान (e) से हुआ।

दो अन्य तुल्य भिन्न हैं 
\(\frac{9 \times 2}{10 \times 2}\) और \(\frac{9 \times 3}{10 \times 3}\) यानी \(\frac{18}{20}\) और \(\frac{27}{30}\)

(iii) \(\frac{660}{990}\) का सरलतम रूप 660 और 990 का म.स. है = 330 
इसलिए \(\frac{660}{990}=\frac{660 \div 330}{990 \div 330}=\frac{2}{3}\)
अतः (iii) का मिलान (a) से हुआ। 

दो अन्य तुल्य भिन्न हैं
\(\frac{2 \times 2}{3 \times 2}\) और \(\frac{2 \times 3}{3 \times 3}\) यानी \(\frac{4}{6}\) और \(\frac{6}{9}\) 

(iv) \(\frac{180}{360}\) का सरलतम रूप 
180 और 360 का म.स. = 180
इसलिए \(\frac{180}{360}=\frac{180 \div 180}{360 \div 180}=\frac{1}{2}\)
अतः (iv) का मिलान (c) से हुआ।

दो अन्य तुल्य भिन्न हैं
\(\frac{1 \times 2}{2 \times 2}\) और \(\frac{1 \times 3}{2 \times 3}\) यानी \(\frac{2}{4}\) और \(\frac{3}{6}\)

(v) \(\frac{220}{550}\) का सरलतम रूप 220 और 550 का महत्तम समावर्तक = 110 
इसलिए, \(\frac{220}{550}=\frac{220 \div 110}{550 \div 110}=\frac{2}{5}\)
अतः (v) का मिलान (b) से हुआ। 

दो अन्य तुल्य भिन्न हैं
\(\frac{2 \times 2}{5 \times 2}\) और \(\frac{2 \times 3}{5 \times 3}\) यानी \(\frac{4}{10}\) और \(\frac{6}{15}\)